11. Задачи и методы измерение парной, частной и совокупной корреляции.

Простейшей системой корреляционной связи является линейная связь между двумя признаками – парная линейная корреляция, т.е. зависимость между двумя признаками. Она рассчитывается по формуле:

Он колеблется от –1 до 1. Если r > 0 – связь прямая, если r < 0 – связь обратная. Чем ближе его абсолютное значение к 1, тем теснее связь.

Уравнение нелинейной регрессии дополняется показателем корреляции – индекс корреляции:

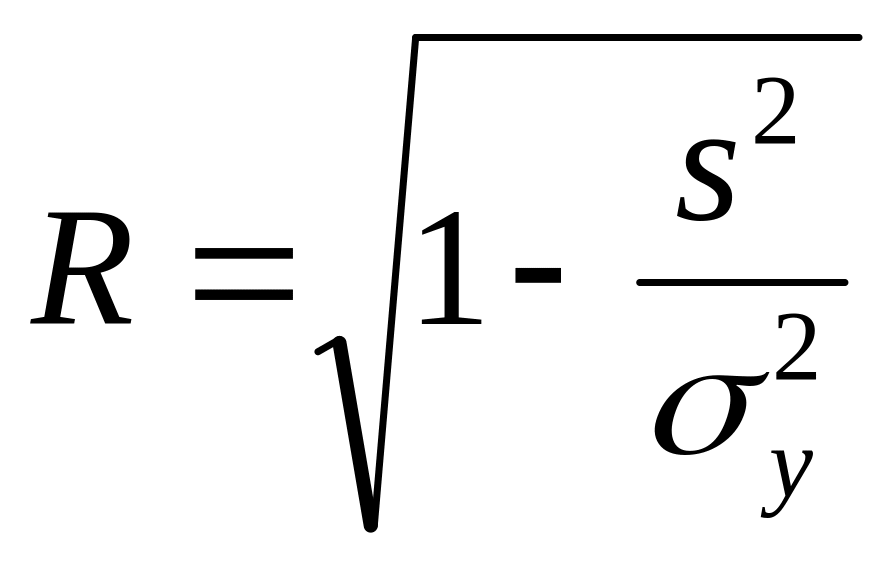
Коэффициент корреляции:

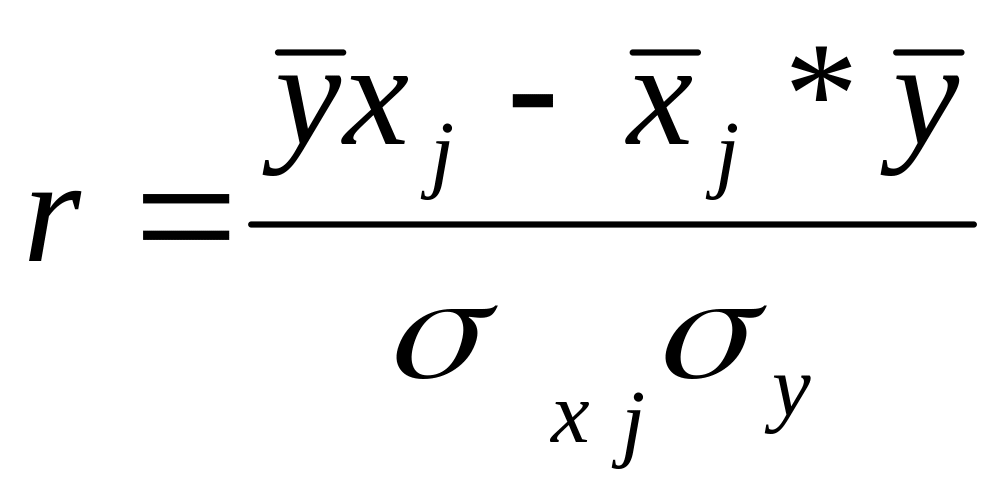
Где _у² - общая дисперсия, S² – остаточная дисперсия.

Величина показателя – от 0 до 1. Чем ближе к 1, тем связь теснее.

При множественной регрессии показатели частной корреляции оценивают тесноту связи результата с соответствующим фактором при устранении воздействия других факторов.

Для изменения тесноты связи результата с каждым фактором в чистом виде т.е. при установлении воздействия других факторов рассчитывается частный показатель корреляции:

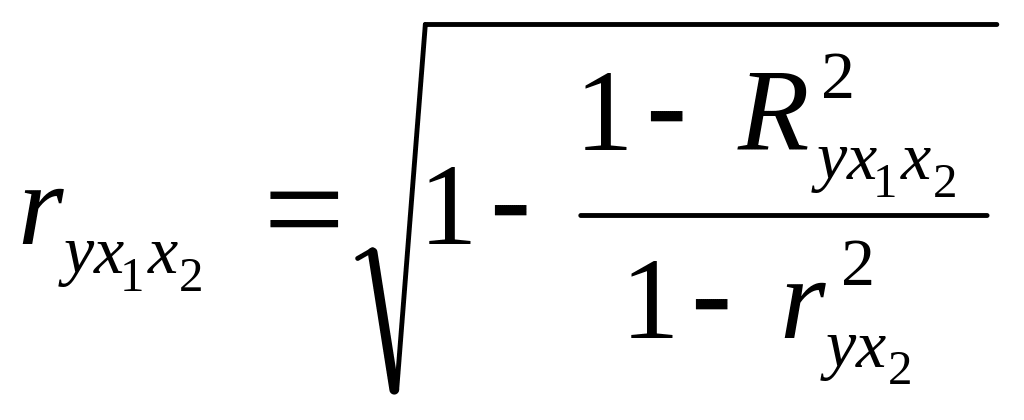
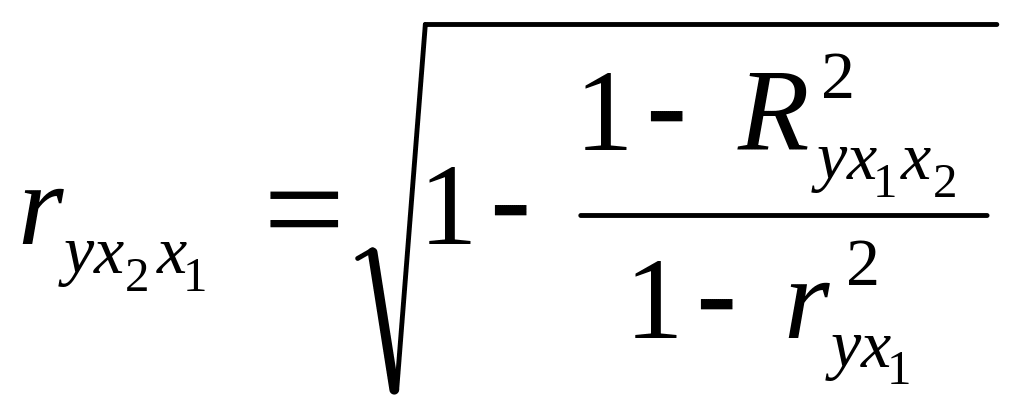
Возможно опред-е частного коэф.корреляции через часные коэф.кор-ии более низких порядков, а в двухфакторном анализе через парные коэф.корреляции по рекуррентной ф-ле:

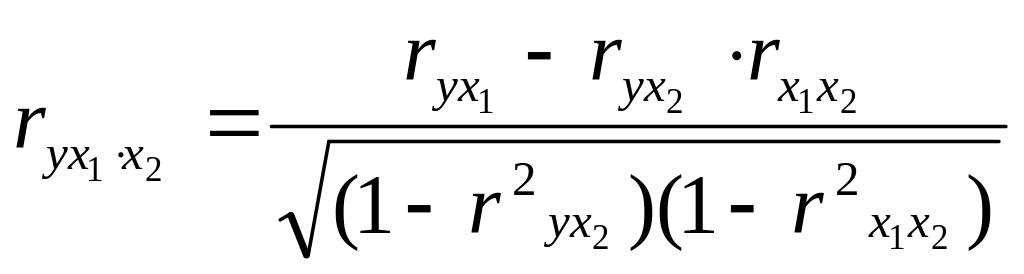
Частные пок-ли корреляции первого порядка, т.е. закрепляется на постоянном уровне 1 фактор; второго порядка-два фактора и т.д.

Чем выше порядок, тем пок-ль корреляции <.

Частные коэф. Корреляции связ. С множественным пок-м корреляции, а именно Ryx1x2x3x4=√1-(1-ryx1^2)*(1-ryx2x1^2)*(1-ryx3x1x2^2)*(1-ryx4*x1x2x3^2).

Множеств.коэф.корреляции всегда больше мах частного коэф.корреляции.

Частная корреляция широко исп-ся на стадии формирования модели. Напр., строя модель методом искл-я переменных на каждом шаге исслед-я отсев факторов происходит во пок-м частной корреляции.

12. Построение регрессионных моделей и их использование в прогнозировании.

Существуют разные методы построения моделей:

1. метод всех возможных регрессий

2. метод исключения

3. метод включения

4. шаговый

1. Метод всех возможных регрессий (Рассм.для построения моделей регрессии с четырьмя переменными y=f(x1;x2;x3;x4)). а) Строятся все возможные парные уравнения регрессии и среди них выбирается наилучшие y=f(x₁), y=f(x₂),у=f(x₃), y=f(x₄).

б) Строятся все возможные двухфакторные уравнения y=f(x₁;x₂) y=f(x₁;x₃) ... y=f(x₃;x₄). Выбирается лучшее по коэффициенту детерминации в соответствии с выбранным в парных уравнениях.

Затем строятся уравнения y=f(x₁;x₂;x₃) y=f(x₁;x₂;x₄) Выбирается наилучшие, учитывая предыдущие действия. Строится уравнение y=f(x₁;x₂;x₃;x₄). Если включение дополнительного фактора не увеличивает существующий коэффициент детерминации, то такой фактор следует признать лишним. Из каждой группы в анализе выделены наилучшие Ур-я регрессии и далее подвергается анализу остаточная дисперсия (она д.б.наименьшей). Ост.дисперсия м.рассматриваться такжеи для каждой рассматриваемой серии уравнений. Метод не гарантирует, что не существует лучшего набора переменных. Чаще на практике исп.др. методы и прежде всего это метод исключения переменных.

2. Метод исключения. На первом этапе строится уравнение со всеми наблюдаемыми переменными, далее оцениваются значимость каждого фактора и отбирается для отсева фактор, имеющий минимальное значение частного коэффициента корреляции, стандартизированного коэффициента регрессии, t критерия, F критерия.

На втором этапе вновь строится уравнение регрессии с учетом оставшихся факторов.

Процедура продолжается до тех пор, пока все параметры уравнения регрессии не окажутся статистически значимы.

3. Метод включения. это обратный метод методу исключения. В модель включ.переменные по очереди до тех пор, пока Ур-е не станет удовлетворительным, т.е все параметры стат.значимы. Начинаем построение модели с м-цы парных коэф.корреляции для полного набора ф-ов. Напр., зав-ть y=f(x₁;x₂;x₃;x₄). Нашли м-цу парных коэф.корреляции и по ней отобрали переменную, кот. С наиб.степенью связ. С рез-ом. Предположим, это х1, далее опред.частные коэф.корреляции 1-го порядка, т.е ryxj*x1 и среди них выбирается мах.величина. Предположим, что мах оказ. Пок-ль ryx2*x1,сл-но далее строим Ур-е регрессии у=f(x1,х2). Для этого Ур-я опред-ся частные коэф.корреляции 2го порядка ryx3*x1x2 и ryx4*x1x2. Предположим, что мах оказ. ryx4*x1x2,сл-но далее на след.шаге включаем в модель ф-р х4, т.е у=f(x1, х2,х4). Для фактора х4 частный Fкрит.оказ-ся стат не значимым, поэтому можно ограничиться уравнением у=f(x1,х2).

Т.о, после того, как каждая переменная введена в модель исслед-ся по модели R^2; общий и частный Fкрит.(для последнего включ.в модель ф-ра частный Fкрит. Показ-ет вносит ли включенная переменная значимый вклад в вариацию результативного признака у сверх того, что имели на предыдущем шаге. Как только частный Fкрит.< Fтабл. Процесс заканчивается.

4. Шаговый регр. Анализ. В отличие от предыдущего метода, в шаг.регрес.анализе на каждом шаге пров-ся исслед-е включ.переменной. Фактор, кот.м.б наилучшим на ранней стадии м.оказаться излишним на более поздней связи из-за взаимосвязи м/д этими факторами и новым фактором, содержащемся теперь в модели. Для этого на каждой стадии опред-ся частный Fкритерий, позволяющий оценить вклад каждой переменной в предположении, что она введена в модель последней.

Любая переем., кот дает незначительный вклад исключается из модели. Процесс прод-ся до тех пор пока никакие перем не доб-ся в Ур-е и не исключаются из него

5. Ступенчатая регрессия. Этапы проведения ступенчатой регрессии след.: а)строится м-ца парных коэф.корреляции и по ней отбир. Переем наиб тесно связ с рез-ом. Предпол, что для моделей y=f(x1 x2 x3 x4) это ф-р х4 (мах коэф.корреляции). Строим Ур-е регр. У=f(x4). Предп.. что ур-е регр.составит у= 117-0,74х4; б) для Ур-я регр У=f(x4) опред. Остатки и находим корреляцию остатков с каждым из ф-ов не вкл.в модель; в) из коэф.корреляции остатков с ф-ми х1,х2,х3 выбир.мах. Предположим, что это ф-р х1 и строим регрессию остатков от ф-ра х1. Е=-10+1,35х1+U. Подставим это выр-е в первое Ур-е у^=107-0.74x4+1.35x1. Для нового Ур-я находим вновь теор зн-я у и новые остатки Е. Эти остаткивновь рассм как зависимую переменную и опред.их корреляцию с факторами, не вкл.еще в модель rex2 и rex3. Если эти пок-ли корреляции сущ-ны, то процедуру прод-ют до тех пор, пока регрессия станет не значимой. В этом случае процесс завершается без вкл.последней перем.

Предположим, что в нашем примере пок-ли корреляции rex2 и rex3 оказ не знач, тогда окончат Ур-е по модели ступ регр сост-ет у^=107-0.74x4+1.35x1

Использование регрессионной модели для прогнозирования состоит в подстановке в уравнение регрессии ожидаемых значений факторных признаков для расчета точечного прогноза результативного признака или его доверительного интервала.

13. Индексы как метод изучения связей и как способ агрегирования.

Индексы – это показатели, которые позволяют оценить изменение одного и того же признака в отчетном периоде по сравнению с базисным.

Базисные данные могут быть разных видов:

1. прошлого пер-да 2) проектные, плановые, нормативные.

Индексы измеряют изменение сложных явлений. Это непросто сравнение двух чисел, а получение и сравнение некоторых агрегированных величин.

С помощью индексов производится факторный анализ, выявляется роль отдельных факторов на результат. признак.

Сравнение отчетных и базовых данных можно проводить в двух формах

• в форме отношения

• в форме разности

В первом случае получают величину, которая показывает во сколько раз отчетные данные больше или меньше базисных.

Если эта величина меньше 1, то произошло снижение от четных данных по сравнению с базисным.

При построении индексов в форме разности из отчетного вычитают базисный.

Различают следующие виды:

1. По степени обобщения единиц совокупности: индивидуальные и сводные.

Индивидуальные строятся или для единицы наблюдения или для отдельного элемента.

Сводные или общие индексы - по массе наблюдений или по нескольким элементам.

2. В зависимости от цели или хар-ра решаемых з-ч - простые и аналитические

Простой – рассчитывается только для соизмеримых признаков.

Аналитич. – анализирует влияние факторов на результат, м.построить для несоизмеримых величин.

3. по методике расчета – индексы в агрегатной форме и индексы средневзвешенные из индивидуальных

Агрегатные - соотношение итоговых подсчетов

Средние из индивидуальных - в основу расчета этих индексов берутся индивидуальные из этих индексов и средние из индивидуальных

Система индексов отражает ту взаимосвязь, кот. сущ-ет м/у изучаемыми признаками. Напр., система признаков – фонд оплаты труда (Ф), среднесписоч. числ-ть раб-х (Т), ср. з/п (L), которые взаимосвязаны: Ф=Т*L. Индексы этих признаков имеют ту же взаимосвязь: Iф=It*Il. Увязка индексов в систему позволяет опр-ть недостающий индекс, если известны 2 других.

Связи м.б. стохастическими (когда у нельзя представить как сумму или произв-е каких-либо величин) и детерминированные.

Инд. метод примен. в стат. также для изучения динамики ср-х величин и выявления факторов, влияющих на динамику ср-х. Это решается с пом. взаимосвязи индексов перемен., пост. состава и стр-х сдвигов.

Инд. перем. сост: (соотношение средних величин какого-либо признака в отчетном и базисном периодах; хар-ет изм-е ср. уровня за счет влияния 2-х факторов: изменения значений осредняемого признака (х) у отдельных ед-ц совокупности и структурных изменении, под кот. Понимается изменение доли отдел.ед-ц сов-ти в общей их численности d=f/∑f)

Инд. пост.состава (отражает изолиров. действие одного фактора)

Инд. стр.сдвигов (хар-ет влияние изм-й структуры изуч-ой совок-ти на динамику ср. уровня признака).

Индексы переем., пост состава и структ. Сдвигов увяз в след с-му.