7. Структурные характеристики распределения. Направления их использования.
Для характеристики среднего значения признака в вариационном ряду исп. Так назыв. Пок-ли центра распред-я. К ним относ-ся средняя величина признака, мода и медиана.
Расчет средней величины признака (хср.) в вариационном ряду осущ-ся по ф-ле средней арифметич.взвешанной : хср.=∑хf/∑f (f-частоты, х-варианты признака).При расчете ср.величины интервального ряда в кач-ве вариантов признака исп-ся значения середины интервалов
Медиана – значение признака находящегося в середине упорядоченного ряда. В интервальном вариационном ряду для нахождения медианы применяется формула.
Х
Ме
– нижняя граница медианного интервала;
i
– величина интервала ;
fi
– сумма совокупности; SMe-1
– накопленная частота в интервале
предшествующем Ме; fMe
– частота в медианном интервале.
Еще один важный показатель – мода. Это значение признака наиболее часто встречаются в совокупности.
XMo - Нижняя граница модаль-го интер-ла; fMo- частота в мод-ом интер-ле; fMo-1- частота в пред-ем интер-ле; fMo+1- частота в след-ем интер-ле за модальным; i – вел-на интервала.
Мода в практике имеет самое широкое применение при изучении покупательского спроса, регистрации цен и т.д. Медиана – в маркетинговой деятельности.
Если распределение по форме близко к нормальному, то медиана находятся между средней и модой. Если x ср > Me > Mo – имеет место правосторонняя асимметрия.
Если x ср < Me < Mo – левосторонняя асимметрия.
К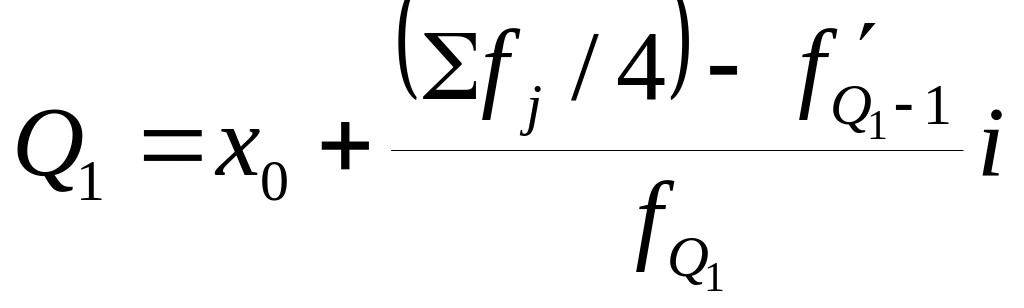
вартили
распределения - аналогично моде
вычисляются значения признака делящие
совокупность на 4 равные части по числу
единиц:
, Q2-медиана, .
На основе квартилей определяют показатель, который оценивает силу вариации не по всей совокупности, а по ее центральной части – это среднее квартильное расстояние:
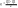
С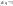
реднее
квартильное расстояние сравнивают с
линейным отклонением:
Если примерно = 1 – вариация признака в центральной части и на периферии имеет небольшое значение.
Значения признака, делящие ряд на пять равных частей называют квинтилями; на 10 частей - децилями.
Данные характеристики часто используются в практике. Например, для распределения населения по доходам по децильным группам.
8. Анализ таблицы сопряженности.
Для исследования связей м/д качественными признаками исп.таблицы сопряженности, т.е таблицы, в кот.дается распределение по 2м или более признакам. При анализе связи м/д признаками каждый из кот. Принимает 2 значения (такие переменные наз.дихотомическими) исп. Таблица сопряженности 2*2. Напр., исследуется связь м/д трудоустройством граждан (рез-т) и опытом их работы(признак фактор).
Для таких таблиц разработаны специальные меры связей. К ним относятся: коэффициент ассоциации, коэф. контингенции.
Коэффициент
ассоциации:
,
Коэффициент ассоц. приним. значения в интервале о 0 до 1: 0 – отсутствие связи, 1- полная связь. Недостаток данного пок-ля: если хотя бы в одной из клеток им.нулевые зн-я, то коэф-т стан-ся = 1.
Более достоверное измерение связи обеспечивает коэффициент контингенции:
Связь считается подтвержденной, если Q>0,5; Ф>0,3.
Если каждый из качественных признаков состоит более чем из 2х групп, то для опред-я тесноты связи м.исп.коэф. взаимной сопряженности Пирсона и Чупрова. Они нах.в пределах от 0 до 1.
;
,
где nij- частоты в клетках таблицы ( i-категория по призн.х, j-категория по пр.y.);
ni – итоговые частоты по строкам; nj-по столбцам.
Недостаток коэф. Пирсона в том, что он не достигает единицы и при полной связи признаков, а лишь стремится к ней при увеличении числа групп.
Более
совершенная мера связи предложена
русским статистиком А.А. Чупровым.
,
m-число строк, p-число столбцов.
Для случая неквадратных таблиц Г. Крамер предложил в формуле коэф. взаимной сопряженности учитывать минимальную из величин: либо число строк без 1, либо число столбцов без 1. Коэф. взаимной сопряженности Крамера имеет вид:
Коэф. Корреляции рангов Спирмена рассчит-ся по ф-ле:
Ρ=1-(6∑d2/n(n2-1), где d – разность рангов по перем.
Х и у. Чем ближе к 1, тем теснее связь.
Очевидно, что в случае квадратной таблицы коэффициенты взаимной сопряженности Чупрова и Крамера совпадают.
Очевидно, что коэффициенты взаимной сопряженности – симметричные меры связей. Все они используются для измерения тесноты связи после того, как факт наличия связи доказан на основе критерия хи-квадрат.