
- •Алгебра та початки аналізу Частина і
- •Харків 2010 Передмова
- •Розділ 1 Числові системи та наближені обчислення
- •§ 1. Натуральні числа
- •§ 2. Звичайні дроби
- •§ 3. Десяткові дроби
- •§4. Пропорція
- •§5. Відсотки
- •§6. Додатні і від’ємні числа. Цілі числа. Дійсні числа. Модуль дійсного числа
- •§7. Дії з алгебраїчними виразами
- •Правило розкриття дужок
- •§8. Лінійні та зведені до них рівняння та нерівності
- •§9. Квадратні рівняння та рівняння, що зводяться до квадратних
- •§10. Квадратні нерівності
- •§11. Наближені обчислення. Абсолютна та відносна похибки
- •§12. Обчислення з наближеними даними. Розв’язання трикутників
- •Розділ 2 Функції, їх властивості та графіки
- •§13 Числова функція. Способи завдання функції
- •§14 Властивості числових функцій
- •§ 15 Обернена функція
- •§ 16 Перетворення графіків функцій
- •§ 17 Границя функції
- •Основні табличні границі
- •Основні теореми про границі
- •Особливі границі
- •§ 18 Неперервність функції
- •Запам’ятайте:
- •Розділ 3 Степені та логарифми
- •§ 19 Степінь з довільним раціональним показником
- •Властивості степенів з раціональним показником:
- •§ 20 Логарифми та їх властивості
- •Властивості логарифмів
- •§ 21 Показникова функція та її властивості
- •§ 22 Логарифмічна функція та її властивості
- •§ 23 Степенева функція та її властивості
- •Функція
- •§24 Показникові рівняння та нерівності
- •§ 25 Логарифмічні рівняння та нерівності
- •Список літератури
§ 2. Звичайні дроби
▼8. Дайте відповіді на запитання:
1) Що називають звичайним дробом і як його позначають?
2) Що показують чисельник і знаменник дробу і як вони розташовані відносно риски дробу?
3) Який дріб називається правильним, а який неправильним?
4) Порівняйте правильний і неправильний дроби з одиницею.
5) Який дріб має назву мішаного дробу, або мішаного числа?
9. Запишіть подані мішані числа у вигляді неправильних дробів:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
10. У поданих неправильних дробів виділіть цілу частину:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
● 11.
I Розгляньте
та проаналізуйте приклади скорочення
поданих дробів
.
● 11.
I Розгляньте
та проаналізуйте приклади скорочення
поданих дробів
![]() ;
;
![]() ;
;
![]() ;
;
![]()
II Сформулюйте основну властивість дробу
12.Скоротіть
подані дроби:
![]()
13. Зведіть дроби до (найменшого) спільного знаменника:
1)
![]() і
і
![]() ;
2)
;
2)
![]() і
і
![]() ;
3)
;
3)
![]() і
і
![]() ;
4)
;
4)
![]() і
і![]() ;
5)
;
5)
![]() і
і
![]() .
.
●14. I Розгляньте та проаналізуйте виконання дій додавання та віднімання дробів
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
;
4) ;
5)
;
5)
 ;
6)
;
6) ;
7)
;
7)
![]() ;
;
8)
 .
.
II Обчисліть:
1)![]() ;
;
2)
![]() .
.
●15. I Розгляньте та проаналізуйте виконання дій множення та ділення дробів
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() .
.
II Виконайте дії:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() . До
змiсту
. До
змiсту
§ 3. Десяткові дроби
▼16. Пригадайте які дроби мають назви десяткових і їх форму запису
●17. Розгляньте та проаналізуйте виконання дій додавання, віднімання, множення та ділення десяткових дробів
1) 0,234 2) 7,459 3) 13,300 4) 0,132 5) 19,2|12__
+3,523 -2,181 -9,674 ×2,34 -12 1,6
3,757 5,278 3,626 528 72
+396 -72
264 0
0,30888
6) 0,192|12 7) 3,456:0,36=345,6|36____
- 12 0,016 -324 9,6
72 216
-72 -216
0 0
▼18. При виконанні дій з дробами може виявитися, що одні числа записані у вигляді звичайних дробів, інші – у вигляді мішаних, треті – у вигляді десяткових. При виконанні дій над такими числами можна або перетворювати десяткові дроби на звичайні або мішані і застосовувати правила дій над звичайними дробами, або перетворювати звичайні і мішані дроби на десяткові ( якщо це можливо) і застосовувати правила дій над десятковими дробами.
I Пригадайте як перетворити десятковий дріб у звичайний і навпаки. Дайте відповіді на такі запитання: 1) Який дріб має назву нескінченного періодичного?
2) Що таке чистий періодичний і мішаний періодичний дроби?
3) За яким правилом переводять нескінченний періодичний діб у звичайний?
II Перевірте свої відповіді за наведеним нижче теоретичним матеріалом
Нескінченний десятковий дріб, у якому, починаючи з деякого розділу, цифри повторюються, називається періодичним. Наприклад, 0,111…, 4,333…, 5,8777…, 9,0131313… . Послідовно повторювана група цифр (мінімальна) після коми називається періодом. Так, 0,111… - період дорівнює 1; 4,333… - період дорівнює 3;
5,8777… - період дорівнює 7; 9,0131313… - період дорівнює 13. Період прийнято записувати один раз, беручи його в круглі дужки: 0,111…=0,(1); 4,333…=4,(3); 5,8777…=5,8(7); 9,0131313…=9,0(13).
Якщо період починається відразу після коми, то дріб називається чисто періодичним; якщо між комою і періодом є інші десяткові знаки, то дріб називається мішаним періодичним. Так, наприклад, 3,(41)=3,414141… - чистий періодичний дріб; 5,8(7)=5,8777… - мішаний періодичний дріб.
Щоб перетворити періодичний дріб у звичайний, треба від числа, що стоїть до другого періоду, відняти число, що стоїть до першого періоду, і записати цю різницю чисельником; у знаменнику написати цифру 9 стільки разів, скільки цифр у періоді, і після дев’яток дописати стільки нулів, скільки цифр між комою і першим періодом. Наприклад:
![]() ;
;
![]()
19. Подайте у вигляді скінченого або нескінченного періодичного дробу:
![]()
Подайте у вигляді звичайного дробу або мішаного дробу наступні нескінченні періодичні десяткові дроби:
0,(51); 1,(13); 0,(25); 2,(125); 0,(113);
0,3(51); 2,12(3); 0,2(125); 1,31(12); 1,252(13).
■ 21. Виконайте дії:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() .
.
22. Обчисліть:
1)
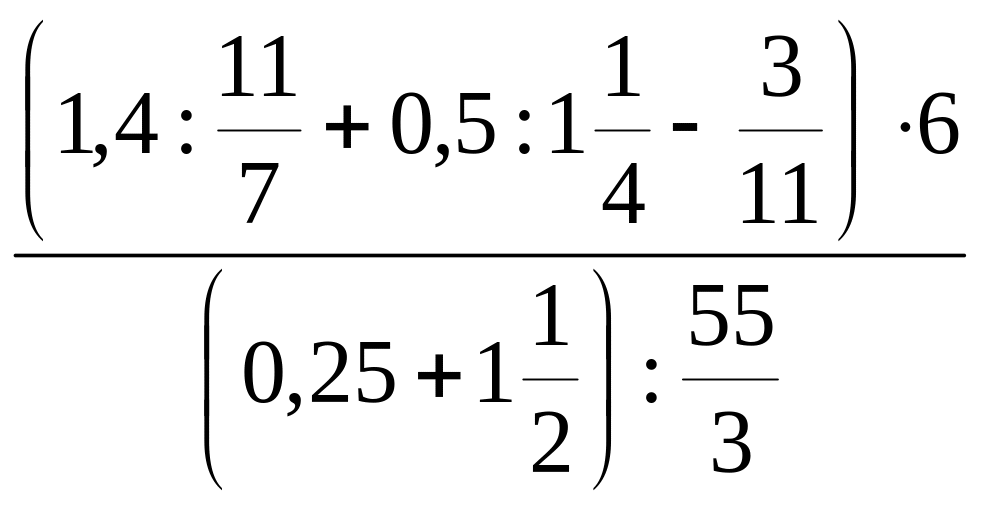 ;
2)
;
2)
![]() ;
;
3)
 ;
4)
;
4)
![]() ;
;
5)
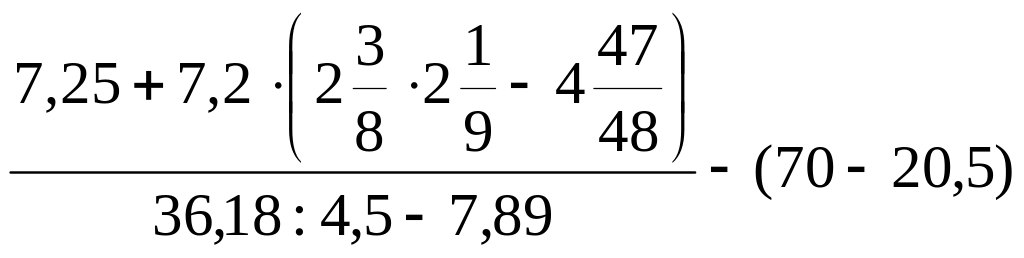 ;
6)
;
6)
 ;
;
7)
 ;
;
8)
 ;
;
9)
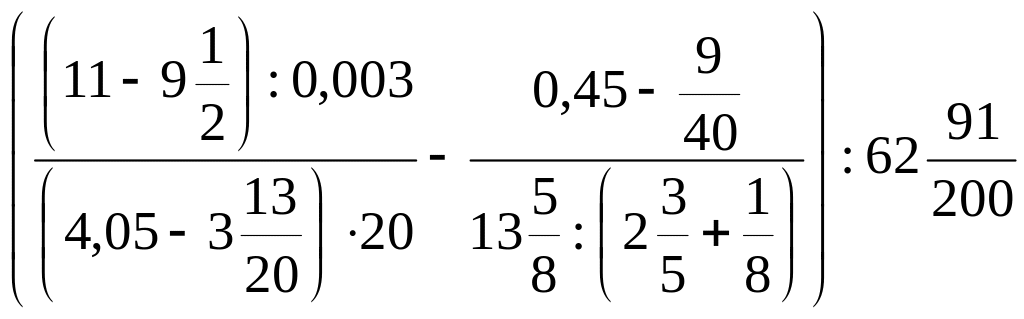 ;
10)
;
10)
 .
.
*23. Знайдіть значення виразу:
1)
 ;
;
2)
 ;
;
3) . До
змiсту
. До
змiсту
