§ 20 Логарифми та їх властивості
Логарифмом
додатного
числа
(
)
за основою
,
називається показник
степеня, до
якого треба піднести основу
,
щоб одержати число
.
Логарифм числа
за основою
позначається символом
.
Наприклад,
;
;
.
Десятковим
логарифмом називається логарифм за
основою 10 і позначається
.
Натуральними
логарифмами називаються логарифми за
основою
(число
-
ірраціональне,
),
позначаються
.
Означення логарифма можна коротко записати так:
.
Ця рівність
справедлива при
і називається основною логарифмічною
тотожністю. Наприклад,
,
.
Властивості логарифмів
Для будь-яких
і будь-яких додатних
і
виконуються рівності:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
149. Знайти:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
150. Знайти значення виразу:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
;
17)
;
18)
;
19)
;
20)
;
21)
;
22)
;
23)
;
24)
;
25)
;
26)
;
27)
;
28)
;
29)
;
30)
;
31)
;
32)
;
33)
;
34)
;
35)
;
36)
.
151. Знайти , якщо:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
До змiсту
§ 21 Показникова функція та її властивості
Функція, задана
формулою
,
де
,
називається показникової.
Властивості
функції
при
:
1) область визначення
– уся числова пряма, тобто
;
2) область значень
– проміжок
,
тобто
;
3) функція не є ні
парною, ні непарною, оскільки
і
;
4) функція зростає
на всій числовій прямій,
;
5) при
значення функції дорівнює 1, тобто
;
6) якщо
,
то
;
7) якщо
,
то
.
Графік функції при виглядає так, як показано на рис. 27
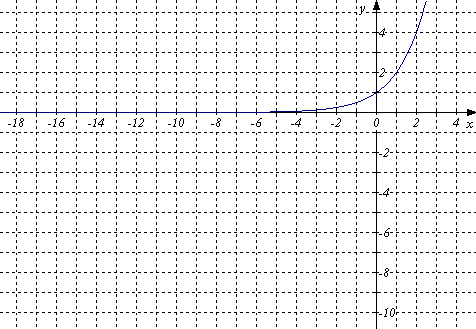Рис. 27
Властивості
функції
при
:
1) область визначення – уся числова пряма, тобто ;
2) область значень – проміжок , тобто ;
3) функція не є ні парною, ні непарною;
4) функція спадає
на всій числовій прямій,
;
5) при значення функції дорівнює 1, тобто ;
6) якщо , то ;
7) якщо , то .
Графік функції
при
виглядає так, як показано на рис. 28
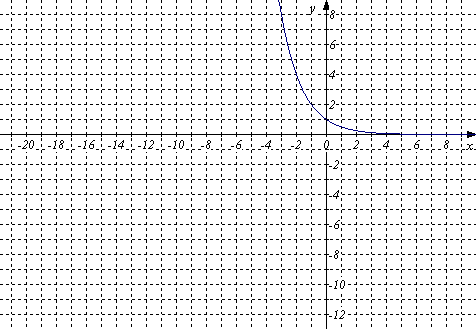Рис. 28
152. Побудувати графіки функцій:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
.
153. Порівняти значення виразів:
1)
і
;
2)
і
;
3)
і
;
4)
і
;
5) 1 і
; 6)
і 1;
7)
і 1; 8) 1 і
;
9)
і
;
10)
і
;
11)
і
;
12)
і
.
154. Порівняти
числа
і
,
якщо:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
155. Порівняти з одиницею, якщо:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
.
До змiсту