Федеральное агентство по образованию
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ГЛАЗОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
имени В.Г. Короленко
ЦЕЛЫЕ НЕОТРИЦАТЕЛЬНЫЕ ЧИСЛА
Материалы
к практическим занятиям по математике
для студентов, обучающихся по специальности
«Педагогика и методика начального образования»
Глазов 2010
ББК
Целые неотрицательные числа: Материалы к практическим занятиям по математике. – Глазов: ГГПИ, 2010. – с.
Составитель: ст. преподаватель кафедры ПиМНО Г.В. Керова
Рецензент: канд. физ.-мат. наук, доцент каф. мат. анализа ГГПИ В.В. Маев
В пособии представлен материал по разделу «Целые неотрицательные числа» для использования на практических занятиях по математике и в самостоятельной работе студентов, обучающихся по специальности «Педагогика и методика начального образования».
Ó Глазовский государственный педагогический институт, 2010
Тема 1. Понятие алгебраической операции. Свойства алгебраических операций Контрольные вопросы по теории
Сформулируйте условия, при которых операция, заданная на множестве Х будет алгебраической.
Каковы особенности частичной алгебраической операции?
В каком случае можно утверждать, что множество замкнуто относительно какой либо операции?
Сформулируйте следующие свойства алгебраических операций: ассоциативность, коммутативность, дистрибутивность, сократимость.
Какими из перечисленных свойств обладают операции сложения, вычитания и умножения на множестве натуральных чисел.
Выясните, как формулируются свойства сложения и умножения в различных учебниках по математике для начальной школы.
В каком случае операции являются обратными?
Дайте определение нейтрального элемента.
Какой элемент является нейтральным для сложения натуральных чисел?
Дайте определение поглощающего элемента.
Какой элемент является поглощающим относительно операции пересечения множеств?
Дайте определение симметричных элементов.
Какие элементы являются симметричными относительно операции сложения?
Практические задания
Объясните, почему сложение и умножение являются алгебраическими операциями на множестве целых неотрицательных чисел, а деление не является.
На множестве Х = {–1; 0; 1} заданы операции сложение, умножение и вычитание. Являются ли они алгебраическими на этом множестве?
Являются ли алгебраическими операции: сложение, умножение, вычитание и деление, заданные на множестве Х, если:
а) Х – множество четных натуральных чисел;
б) Х – множество нечетных натуральных чисел;
в) Х – множество натуральных чисел, кратных 5?
Среди следующих высказываний укажите истинные, ответ обоснуйте:
а) множество натуральных чисел замкнуто относительно умножения;
б) множество рациональных чисел замкнуто относительно деления (деление на нуль не рассматривается);
в) множество целых чисел замкнуто относительно вычитания и деления;
г) множество целых чисел замкнуто относительно вычитания или деления.
Являются ли алгебраическими на множестве натуральных чисел следующие операции:
а) возведение в степень;
б) нахождение наибольшего делителя;
в) нахождение наименьшего общего кратного?
Дано множество {а, b, с}. Составьте множество Х всех его подмножеств. На этом множестве Х рассмотрите операции пересечения и объединения. Являются ли они алгебраическими?
В начальном курсе математики сложение рассматривают сначала на отрезке натуральных чисел от 1 до 9 (включительно), затем на отрезке от 1 до 100, затем от 1 до 1000. Является ли операция сложения алгебраической на этих множествах?
Коммутативны ли следующие алгебраические операции:
а) возведение в степень на множестве N;
б) деление на множестве Q;
в) нахождение наибольшего общего делителя натуральных чисел?
Ассоциативны ли следующие алгебраические операции:
а) возведение в степень на множестве N;
б) вычитание на множестве Q;
в) нахождение наименьшего общего кратного натуральных чисел?
Является ли деление на множестве положительных действительных чисел дистрибутивным относительно операции сложения?
Является ли операция объединения множеств дистрибутивной относительно операции пересечения множеств? Ответ обоснуйте.
Докажите, что операция возведения в степень на множестве натуральных чисел дистрибутивна справа относительно умножения.
Является ли вычитание целых чисел дистрибутивной операцией относительно умножения?
Является ли операция вычитания множеств дистрибутивной относительно операции пересечения множеств? Ответ поясните с помощью диаграмм Эйлера-Венна.
Сократимо ли вычитание и деление на множестве рациональных чисел?
Какое множество является поглощающим элементом относительно пересечения множеств? Ответ обоснуйте.
Какое число является нейтральным относительно операции сложения целых чисел? Есть ли нейтральный элемент для сложения натуральных чисел?
Какое число является нейтральным относительно операции умножения целых чисел?
Какое множество является нейтральным элементом относительно операции объединения множеств? Существует ли нейтральный элемент для операции пересечения множеств (рассматриваются лишь подмножества универсального множества).
Какое число симметрично числу 8 относительно операции сложения натуральных чисел? А числу – 6?
Какое число симметрично числу 8 относительно операции умножения рациональных чисел? А числу –
?
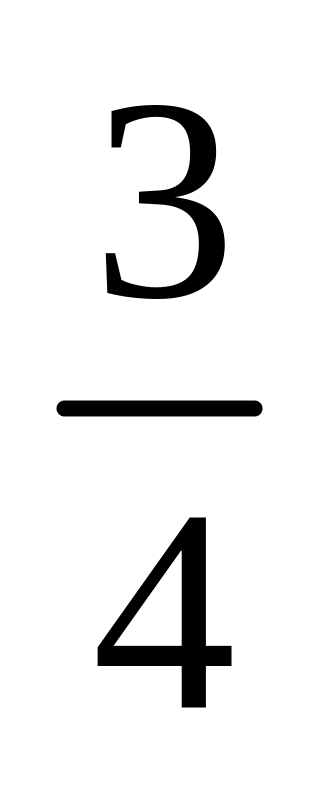