4. Динамика абсолютно твердого тела Лекция № 6

4.7. Основное уравнение динамики вращательного движения относительно неподвижной оси.

4.8. Расчет моментов инерции.

4.9. Кинетическая энергия вращающегося тела.

4.10. Работа силы при вращении тела.

4.7. Основное уравнение динамики вращательного движения относительно неподвижной оси

Р ассмотрим вращательное движение твердого тела относительно неподвижной оси Oz. Так как твердое тело можно представить как совокупность материальных точек, то воспользуемся основным уравнением динамики вращательного движения относительно точки (4.3.8).

. (4.7.1)

Найдем проекции правой и левой части уравнения (4.7.1) на ось Оz:

. (4.7.2)

. (4.7.3)

Вектор перпендикулярен радиус-вектору и образует с осью и образует с осью Оz угол _I = 90° − _I . Поэтому проекция момента импульса материальной точки равна

. (4.7.4)

Подставим правую часть уравнения (4.7.4) в (4.7.3)

. (4.7.5)

Используя , получим момент импульса твердого тела относительно неподвижной оси Оz

L_z = I_z . (4.7.6)

Подставляя (4.7.6) в выражение (4.7.1)

 (4.7.7)

и учитывая, что , получим основное уравнение динамики вращательного движения относительно неподвижной оси

или . (4.7.8)

Угловое ускорение при вращении твердого тела относительно неподвижной оси прямо пропорционально результирующему моменту внешних сил относительно этой оси и обратно пропорционально моменту инерции тела относительно этой же оси.

Физический смысл момента инерции можно определить из выражения (4.7.8). Если сравнить с основным уравнением динамики поступательного движения (2.1.2), то можно увидеть что роль массы при вращательном движении выполняет момент инерции. Момент инерции тела является мерой инерции тела при вращательном движении.

Если проекция моментов внешних сил относительно оси Оz равна нулю (например, система замкнута) , то получаем закон сохранения проекции момента импульса

 . (4.7.9)

Если проекцию моментов внешних сил относительно оси z равна нулю, то момент импульса тела относительно этой оси с течением времени не будет изменяться.

4.8. Расчет моментов инерции

1) Момент инерции однородного полого цилиндра.

Определим момент инерции однородного полого цилиндра, внешний радиус которого R₂ , а внутренний радиус R₁ , относительно оси симметрии. Разобьем цилиндр на концентрические цилиндрические кольца толщиной dr. Все кольца находятся на одинаковом расстоянии от оси, равном r. Если плотность вещества постоянна, то элементарная масса dm = dV, где dV − объем бесконечно тонкого кольца радиусом r, толщиной dr и высотой h. Поскольку dV = (2r)hdr, то dm = 2rhdr.

Т аким образом, момент инерции получается посредством интегрирования по всем кольцам:

= .

Поскольку , то момент инерции равен

.

Объем полого цилиндра , тогда его масса .

Таким образом, момент инерции полого цилиндра

. (4.8.1)

2) Момент инерции тонкостенного цилиндра (обода). Используя формулу (4.8.1) и учитывая, что R₁ = R₂ = R, получим

I = mR ². (4.8.2)

3) Момент инерции однородного сплошного цилиндра (диска). Используя формулу (4.8.1) и учитывая, что в этом случае R₁ = 0 и R₂ = = R, то момент инерции

. (4.8.3)

4) Момент инерции однородного шара.

Определим момент инерции однородного твердого шара радиусом R, относительно оси, проходящей через его центр. Разобьем шар на бесконечно малые цилиндры высотой dy. Каждый такой цилиндр имеет радиус . Тогда массу бесконечно малого цилиндра можем определить как

d m = dV = Sdy = r²dy =

= (R² − y²)dy.

Следовательно, момент инерции любого бесконечно малого цилиндра можно записать в виде:

= .

Интегрируя по всем бесконечно малым цилиндрам, получим:



 .

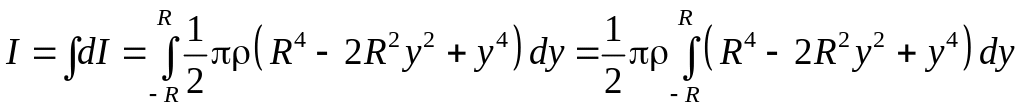
Поскольку объем шара равен , то его масса m = V = = . Таким образом, момент инерции шара будет равен

. (4.8.4)

5) Момент инерции однородного стержня. Момент инерции стержня длиной l относительно оси проходящей через середину стержня перпендикулярно его длине:

. (4.8.5)