3. Общие свойства уравнения Лапласа

3.1. Классификация уравнения

Уравнение Лапласа в декартовой системе координат записывается . Проведем классификацию этого уравнения по признакам, рассмотренным ранее:

1. Порядок уравнения – второй.

1. Число переменных – три.

2. Линейность – линейное.

3. Однородность – однородное.

4. Вид коэффициентов – уравнение с постоянными коэффициентами.

5. Тип уравнения – уравнение эллиптического типа, поскольку

3. 2. Физический смысл оператора Лапласа

Оператор Лапласа ∆ является одним из важных операторов математической физики. Возникает вопрос о смысле оператора и о том, какое отношение имеет сумма трех частных производных второго порядка к законам природы? Ответы на эти вопросы связаны с тем фактом, что лапласиан функции позволяет оценить значение функции в точке через значение функции в соседних точках. Кроме того, лапласиан можно считать обобщением второй производной функции одной переменной на многомерный случай.

Основные свойства двумерного оператора ∆:

1. Если ∆ в точке , то меньше среднего значения функции в соседних точках, например, на окружности с центром в точке .

2. Если ∆ в точке , то равна среднему значению функции в соседних точках.

3. Если ∆ в точке , то больше среднего значения функции в соседних точках.

Рассмотренное свойство может быть обобщено на трехмерное пространство. Таким образом, если функция удовлетворяет уравнению Лапласа ∆ , то ее значение всегда совпадает со средним значением. Например, натянутая неподвижная резиновая мембрана удовлетворяет уравнению Лапласа, следовательно, смещение мембраны в любой точке равно среднему смещению мембраны на окружности с центром в этой точке.

3.3. Особенности решения

В отличие от ОДУ, искомая функция в которых есть функция одной независимой переменной, а число независимых решений определяется их порядком, уравнения Лапласа и Пуассона являются УЧП, и им удовлетворяет множество функций. Другими словами, уравнения Лапласа и Пуассона имеют множество решений, выражающимися разными функциями. Так, например, непосредственной подстановкой в уравнение Лапласа можно убедиться, что ему удовлетворяют следующие функции:

. (3.19)

Поэтому при анализе поля прежде всего необходимо сформулировать те условия, при которых эти уравнения имеют единственное решение.

3.4. Граничные условия

Решение уравнения Лапласа станет однозначным, если наложить на задачу дополнительные, так называемые граничные условия (ГУ). Этими условиями являются значения зарядов, величин потенциалов, токов, температуры, так или иначе ограничивающих пространство поля (рис. 3.2).

Граничные условия определяются только из физической постановки задачи. Для стационарных потенциальных полей все возможные ГУ могут быть сведены к трем наиболее важным типам:

1. Первого рода (условие или задача Дирихле);

2. Второго рода (условие или задача Неймана);

3. Третьего рода (условие или задача Робена).

В отличие от гиперболического волнового уравнения и параболического уравнения теплопроводности эллиптические уравнения не требуют начальных условий (НУ). Для них нужны только граничные условия. По этой причине задачи для этих уравнений называются еще и краевыми задачами.

Рассмотрим основные типы граничных условий в краевых задачах.

1. Краевая задача с граничными условиями первого рода (задача Дирихле).

Задача возникает, когда требуется найти решение уравнения в некоторой области пространства, которое принимает на границе области заданные значения. В качестве примера можно рассмотреть задачу о нахождении стационарного распределения температуры внутри области, если известен потенциал на границе. Задачи такого типа называют внутренними задачами Дирихле (см. рис. 3.2).

Δ

ф

Рис. 3.2. Внутренняя задача Дирихле Рис. 3.3. Внешняя задача Дирихле

Помимо внутренней задачи Дирихле различают внешнюю задачу Дирихле, для которой решение уравнения Лапласа ищется вне круга, а граничные условия заданы на окружности.

В общем случае первая краевая задача формулируется так: найти функцию , удовлетворяющую уравнению ∆ , внутри объема и принимаемую в каждой точке поверхности заданные значения :

. (3.20)

Выражение (3.20) и есть математическая формулировка граничного условия в краевой задаче Дирихле.

2. Краевая задача с граничными условиями второго рода (задача Неймана).

Задача возникает тогда, когда требуется найти решение уравнения в некоторой области пространства, на границе которой задана внешняя нормальная производная , которая пропорциональна втекающему потоку, например тепла, электронов, диффундирующих частиц и т.д. Математическая формулировка краевого условия второго рода выглядит так:

. (3.21)

В общем случае вторая краевая задача выглядит так: найти функцию , удовлетворяющую уравнению Δ , внутри объема , нормальная производная которой принимает в каждой точке поверхности заданные значения .

3. Краевая задача с граничными условиями третьего рода (задача Робена).

Задача возникает тогда, когда требуется найти такое решение уравнения в некоторой области пространства, которое удовлетворяет на границе условию

, (3.22)

где – внешняя нормальная производная; h – заданная константа;

g – заданная функция, которая, вообще говоря, меняется вдоль границы. По сути, это граничное условие является суммой граничных условий первых двух типов. Еще его записывают так:

. (3.23)

Согласно этому граничному условию, если речь идет, например, о тепловом поле, поток тепла, вытекающий в область через границу, пропорционален разнице между температурой U и некоторой заданной температурой g (рис. 3.4). Это означает, что при h > 0:

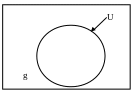
Рис. 3.4. Интерпретация задачи Робена

1. если температура на границе выше температуры окружающей среды на границе g, то тепло вытекает из области;

2. если U < g , то тепло втекает в область.