11. Метод интегральных уравнений

Определение потенциала по заданным его значениям или по значениям его производной по нормали на некоторой поверхности или на кривой может быть выполнено разными методами. В предыдущем разделе обсуждался метод, связанный с формулой Грина. Теперь ознакомимся с применением интегральных уравнений для этой цели.

Приведем классификацию линейных интегральных уравнений.

1. Интегральное уравнение Фредгольма второго рода.

Уравнение вида

, (11.304)

где y(x) – искомая функция; f(x) и k(x, s) – известные функции; D – фиксиро-ванная область с ;  – числовой параметр, называется интегральным уравнением Фредгольма второго рода.

Уравнение (11.304) называется однородным, если f(x)=0, в противном случае – неоднородным.

2. Интегральное уравнение Фредгольма первого рода.

Уравнение вида

, (11.305)

где y(x) – искомая функция; D – фиксированная область с ; называется интегральным уравнением Фредгольма первого рода.

Функция k(x, s) называется ядром интегрального преобразования. Ядро k(x, s) называется вырожденным, если оно представлено в виде

, (11.306)

где функции _i(x) и _i (S) (i =1,2,…., n) линейно независимы в области D или на отрезке [a, b].

Интегральные уравнения Фредгольма (11.304) и (11.305) решаются численными методами с помощью ЭВМ. Обычно используют два приближенных метода решения интегральных уравнений Фредгольма: метод конечных сумм и метод, основанный на аппроксимации ядра уравнения K(x,s) вырожденным ядром.

3. Идея метода конечных сумм заключается в замене определенного интеграла конечной суммой с помощью одной из квадратурных формул

, (11.307)

где x_{j –} абсциссы точек отрезка [a,b]; A_j (j=1,2,…n) – коэффициенты квадратурной формулы, не зависящие от F(x).

Заменяя приближенно интеграл в уравнениях Фредгольма (11.304) и (11.305) по формуле (11.307) и полагая x=x_j , будем иметь соответственно

(i=1, 2,..n), (11.308)

(I=1, 2,..n), (11.309)

где y_i =y(x_i), K_ij=K(x_i, x_j), f_i =f(x_i).

В итоге будем иметь системы линейных алгебраических уравнений относительно значений y_i. Решив эти системы одним из известных методов, получим таблицу приближенных значений y_i в точках x_i. Это позволит записать приближенное решение (11.305) в виде интерполяционного многочлена, а приближенное значение (11.304) в виде

. (11.310)

4. Идею метода замены ядра на вырожденное рассмотрим на примере интегрального уравнения Фредгольма второго рода. Заменим приближенно ядро K(x,s) вырожденным и будем искать приближенное решение уравнения (11.304) в виде

, (11.311)

. (11.312)

Подставляя выражение (11.311) в (11.312), получим

, (11.313)

где i=1, 2,…n.

Вводя обозначение

, (11.314)

получим

(i=1, 2,…n). (11.315)

Получаем систему линейных алгебраических уравнений относительно C_i. Решив эту систему, записываем приближенное решение уравнения (11.304) в виде (11.311) . В качестве вырожденного ядра можно взять отрезок ряда Тейлора или ряда Фурье для функции K(x,s).

Р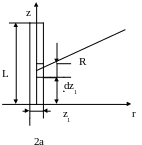 ассмотрим конкретный пример. Требуется определить линейную плотность заряда  вдоль уединенного провода длиной L=50 мм и диаметром 2a=1 мм. Потенциал провода относительно бесконечной удаленной точки равен U. Рассчитаем емкость провода.

Рис. 11.42. К расчету линейной плотности заряда уединенного провода.

Решение

1. Воспользуемся декартовой системой координат, полагая, что плоскость zor проходит через осевое сечение провода (рис. 11.42). Поле вокруг заряженного проводника по своей структуре аксиально-симметричное и зависит от координат r и z, поэтому можно считать, что весь заряд находится на оси провода, его линейная плотность (z).

2. На оси провода – на расстоянии z₁ от начала координат – выделим элемент dz₁, его элементарный заряд будет (z₁)dz₁. Потенциал этого элементарного заряда в произвольной точке наблюдения M запишется как

, (11.316)

где R= .

3. Потенциал поля всего заряженного провода запишется так:

, (11.317)

Для точки M , находящейся на поверхности провода (r = a), по условию задачи потенциал =U

, (11.318)

или

. (11.319)

4. По своей конструкции уравнение (11.318) – интегральное, неоднородное уравнение Фредгольма первого рода относительно неизвестной функции (z) c ядром , аналогичное (11.305). Решаем эти уравнения методом алгебраизации.

5. Разобьем провод на n одинаковых участков с зарядами _i и будем считать, что внутри каждого участка _i постоянно. Точку наблюдения j, потенциал которой U, выберем по середине провода. Для пояснения хода решения положим n=5. Для того чтобы точка j соответствовала середине участка провода при любом n, необходимо положить z=L(2j-1)/2n. Тогда при n, равном, например 5, средний участок будет иметь номер j, определяемый из решения уравнения 2j-1/n =1, j=n+1/2 =3. Таким образом, выражение (11.318) заменяется равенством

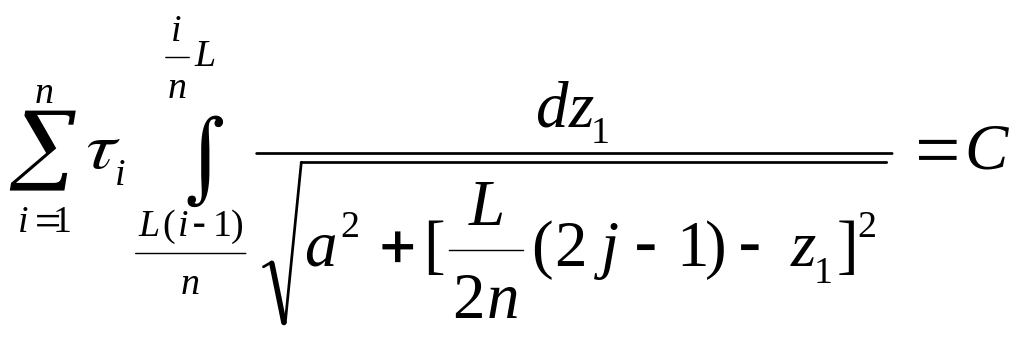. (11.320)

Таких уравнений можно составить в количестве n. В итоге приходим к системе уравнений вида

, (11.321)

где – квадратная матрица коэффициентов; – матрица-столбец искомых линейных плотностей зарядов на участках; – единичная матрица-столбец.

6. Для нахождения элементов матрицы a_ij необходимо взять интеграл в правой части равенства (11.320). Интеграл

(11.322)

может быть преобразован к табличному виду

,

где .

Таким образом,

= .

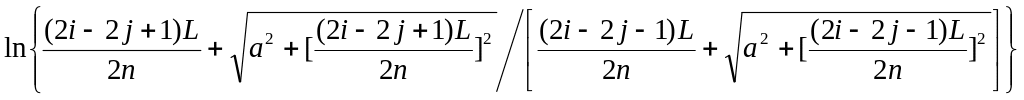(11.323)

7. Для ij, учитывая, что a L , слагаемым под корнем квадратным в уравнении (11.323) можно пренебречь (проверка осуществляется непосредственной подстановкой данных задачи), поэтому окончательно получаем

. (11.324)

8. Для i=j уравнение (11.323) упростится до вида

. (11.325)

В этом выражении .

С учетом того, что a << L, слагаемое .

Воспользуемся известной формулой

при <<1. (11.326)

Тогда .

Числитель дроби под знаком натурального логарифма в выражении (11.325) запишется

. (11.327)

Знаменатель этой дроби

. (11.328)

Окончательно

.

При этом выполняется приближенное условие

. (11.329)

9. Вычисления по (11.324) и (11.329) при n=5 дают матрицу коэффициентов

(11.330)

10. Вследствие симметрии расположения зарядов ₁₌_5, ₂₌₄ относительно ₃ вместо (11.330) можно записать матрицу

(11.331)

Элементы матрицы (11.331) получены из матрицы (11.330) путем преобразования, обусловленного симметрией расположения зарядов

(11.332)

11. Решение задачи теперь сводится к решению системы уравнений

. (11.333)

11. 1. Вычисляем определитель матрицы системы, т. е.

.

11.2. Находим алгебраические значения элементов этого определителя

11.3. Элементы обратной матрицы :

Обратная матрица

Таким образом,

11.4. Окончательно

₁₌₅₌ (0,169-0,035-0,008)=0,126 С,

₂=₄=(-0,035+0,171-0,028)=0,108 С,

₃=(-0,016-0,057+0,178)=0,105 С.

12. Заряд провода

.

13. Емкость провода

.