10. Метод функции Грина решения краевых задач для уравнений эллиптического типа

Метод функции Грина позволяет свести решение уравнений Лапласа или Пуассона в краевых задачах Дирихле, Неймана, Робена (раздел 3.4) к расчету поля точечного или (для плоской задачи) линейного источника при надлежаще выбранных однородных граничных условиях. Решения краевых задач для рассматриваемой области даются формулами, в которых искомый потенциал определен через функции Грина. Для рассмотрения сущности метода предварительно получим формулы Грина и введем понятие о δ (дельта) - функции.

10.1. Формулы Грина

1.Формулы Грина выводят из теоремы Остроградского – Гаусса:

, (10.267)

где D_n – нормальная составляющая вектора на поверхности , ограничивающей объем V. Направление D_n совпадает с направлением внешней нормали по отношению к объему V.

2. Положим , где α – произвольный скаляр, а вектор представим как градиент некоторой тоже скалярной функции φ, тогда

. (10.268)

3. Подстановка (10.268) в (10.267) дает

. (10.269)

4. Проекция вектора на направление нормали есть , с учетом этого тождество (10.269) примет вид

. (10.270)

Формула (10.270) называется первой формулой Грина.

5. Скаляры α и φ в формуле (10.270) можно поменять местами

. (10.271)

Из равенства (10.270) вычтем равенство (10.271), получим вторую формулу Грина

. (10.272)

7. Окончательно вторую формулу Грина можно записать в виде

. (10.273)

10. 2. Применение аппарата δ - функций в электродинамике

До сих пор нами использовались понятия непрерывного распределения плотностей зарядов и токов. На практике часто приходится исследовать поля, возбуждаемые точечными зарядами и точечными излучателями (токами). Чтобы сохранить удобное в физическом и математическом отношении понятие плотностей зарядов и токов для точечных величин, в физике используют аппарат δ - функций. Рассмотрим некоторый объем V, в котором имеется электрический заряд q. Будем уменьшать объем так, что он постепенно «стягивается» до нулевого объема вокруг точки Р₀ ( ). Тогда объемная плотность заряда ρ стремится к нулю во всех точках Р, кроме точки Р₀, в которой она стремится к бесконечности. Если использовать δ - функцию, которую считаем равной нулю во всех точках кроме точки Р = Р₀, где она обращается в бесконечность, то плотность заряда можно записать так: ρ=q δ(Р, Р₀). Действительно, тогда заряд в объеме V представляется выражением

. (10.274)

Для трехмерной δ - функции основное свойство записывают так

. (10.275)

Если положить в (10.275) f(P₀)=1, то получим

. (10.276)

В декартовой системе координат, где dV=dx dy dz, поэтому

. (10.277)

В сферической системе координат dV=R² sinθ dR dθ dφ, поэтому

. (10.278)

В цилиндрической системе координат dV=r dr d φ dz, поэтому

. (10.279)

Теперь мы готовы к обсуждению сущности метода функции Грина.

10. 3. Сущность метода функций Грина

Наша цель: показать, как с помощью функции Грина (функции источника, функции влияния) решают неоднородную задачу Дирихле, т.е. уравнение Пуассона.

Основная идея метода: правая часть уравнения рассматривается как некоторое входное воздействие и разлагается в непрерывную совокупность дельтаобразных источников, распределенных по некоторой заданной области. Затем находится отклик системы на каждый такой источник (функция Грина) и все отклики суммируются (интегрируются). В результате получают полное решение задачи. Физическое содержание сущности метода наиболее наглядно иллюстрируется при решении типичной задачи – определение потенциала в круге в двумерном случае.

1. В такой задаче потенциал удовлетворяет уравнению Пуассона, например, с нулевыми граничными условиями, записанному в полярных координатах

, (10.280)

0<r<1; ; U(1,θ)=0.

2. Заменим правую часть f(r,θ) уравнения (10.280) единичным точечным источником, помещенным в некоторую произвольно выбранную точку P₀(ρ,φ). Математически такой источник представляется δ - функцией δ(r-ρ,θ-φ). По определению, дельта – функция, равная нулю всюду, кроме точки P₀(ρ,φ). Наша задача – найти потенциал точечного заряда, если известно, что на границе он равен нулю. Функция, удовлетворяющая этим условиям, называется функцией Грина или функцией источника. Она равна отклику системы в точке P(r,θ), где r – расстояние от заряда до точки наблюдения. В зависимости от природы анализируемого поля искомый потенциал может иметь следующий физический смысл:

а) в теории теплопроводности – это равновесная температура внутри круга, если тепловой источник размещен в точке P₀(ρ,φ), а на границе поддерживается нулевая температура;

б) описывает отклонение мембраны от положения равновесия, если отклонения на границе равны нулю, а в точке P₀(ρ,φ) мембрана оттянута на очень большую высоту;

в) в электростатике – это распределение потенциала внутри круга, если точечный положительный заряд помещен в точку P₀(ρ,φ), а круг заземлен и его потенциал поддерживается равным нулю. Графически функцию Грина можно представить так, как это показано на рис. 10.39.

3. Функция является потенциалом поля в точке P(r, ), которое создано единичным точечным зарядом, помещенным в точку P₀(,), R – расстояние между точками P и P₀ и единственное, что теперь нужно сделать – так изменить эту функцию, чтобы она обращалась в нуль на границе.

Примечание. Функция для двумерного пространства действительно является решением уравнения Пуассона, что можно проверить непосредственной подстановкой. В действительности, потенциал, равный , на окружности создается полем заряженной оси, т.е. линейным источником с единичным зарядом на единицу длины. С учетом этих замечаний все рассуждения, приведенные выше, остаются правомерными.

4 . Для построения функций Грина снаружи круга размещаем другой (отрицательный) заряд таким образом, чтобы полный потенциал на окружности r = 1 был равен некоторой постоянной величине. Вычтя из полного потенциала эту величину, получим нулевой потенциал на границе. Тогда найденный таким образом потенциал будет удовлетворять всем требованиям, предъявленным к функции Грина G(r,,,). Необходимые построения приведены на рис. 10.40. Остается неясным, в какой точке вне круга нужно разместить отрицательный

заряд, чтобы потенциал на окружности остался постоянным

5. По существу нам нужно выполнить построение функции Грина методом отражения. Этот метод является одним из способов построения функций Грина при решении задач анализа поля. Обозначим через точку, симметричную точке P₀, относительно границы области (окружности С). Точка называется симметричной точке Р₀ относительно окружности, если обе эти точки лежат на одном луче, выходящем из центра круга, и произведение их расстояний  и ₁ равно квадрату радиуса, т.е. ₁= r² =1. Отсюда ₁=1/ . Полный потенциал в соответствии с рис. 10.40.

. (10.281)

6. На примере рис. 10.40 можно показать, что величина потенциала на окружности равна , т.е. положительная константа. Для точки К, например, U_K=U_Q-U_-Q .

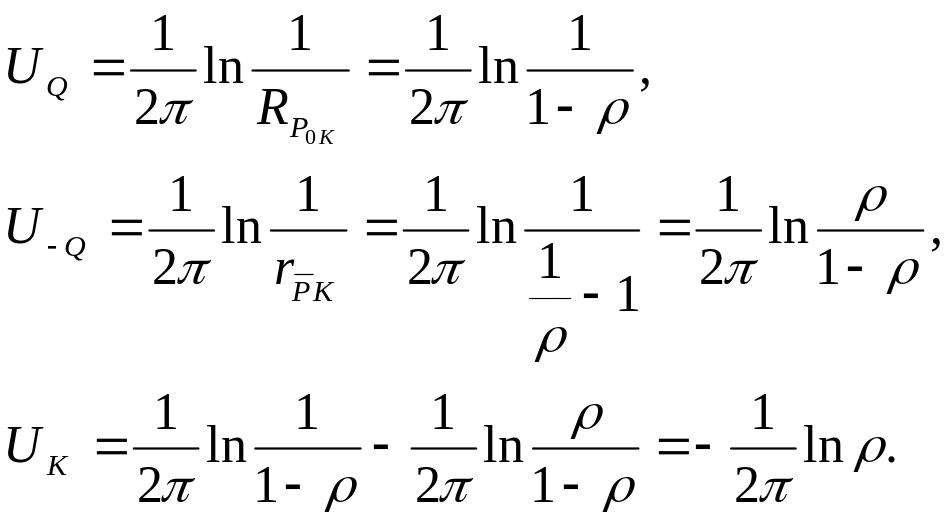
7. С учетом полученных результатов строим функцию Грина:

. (10.282)

В выражении (10.282) первое слагаемое – потенциал положительного заряда, расположенного в точке Р₀ , второе слагаемое – потенциал положительного заряда, расположенного в точке Р, третье слагаемое – вычитание постоянного потенциала границы.

8. Чтобы найти решение исходной задачи, осталось провести сложение всех импульсных откликов системы по формуле

. (10.283)

Формула (10.283) выражает решение задачи Дирихле для уровня Пуассона внутри единичного круга через функцию Грина. Если плотность зарядов f(r,) известна, то интеграл можно вычислить на ЭВМ. Исходя из структуры решения (10.282), функцию Грина можно представить в виде

, (10.284)

где ν – гармонична в искомой области (т.е. удовлетворяет уравнению Лапласа, ν = 0), как функция точки М, а функция (R_PP0) имеет особенность в точке Р₀ , т.е. при R_MP=0 и должна удовлетворять уравнению =-(Р, Р₀). Рассмотрим для определенности трехмерный случай.

Определение потенциала через функцию Грина в общем случае:

1. Математическая формулировка задачи

в V, . (10.285)

2. Метод функции Грина решения таких задач состоит в следующем. Сначала находят решение задачи (10.285) при специальных значениях функции f(M) и U_s. А именно, находят решение G задачи

. (10.286)

Это решение называют функцией Грина задачи (10.285).

3. Если функция Грина найдена, то с ее помощью легко найти и решение исходной задачи (10.285). Для этого применим вторую формулу Грина (10.273) к функциям  = G(M, P) и к искомому решению  = U(M).

. (10.287)

Поскольку в области V имеем U = f(M), а G = -(M, P), то соотношение (10.273) можно записать в виде

. (10.288)

Второй интеграл в левой части по свойству  - функции (10.275) равен U(P), поэтому (10.287) можно записать

. (10.289)

Здесь интегрирование ведется по координатам точки М.

4. Для первой краевой задачи (задачи Дирихле)

G_S=0, U_S=U₀f₁(S), f(M)=-(V)/_a, (10.290)

где  (V) – объемное распределение источников поля. Тогда

. (10.291)

Вывод 1. Если на замкнутой поверхности S, являющейся внешней границей области V, среды с материальной характеристикой _а , задано распределение потенциала U_S = U₀f₁(S), а внутри этой поверхности – объемное распределение источников  (V), то решение задачи Дирихле для рассматриваемой области дается формулой

, (10.292)

где U(P) – потенциал в произвольной точке Р внутри поверхности S;

G – функция Грина, выражающая потенциал единичного точечного источника, расположенного в точке Р, при нулевом значении потенциала на поверхности S;

N – внешняя нормаль к поверхности S.

5. Для второй краевой задачи (задачи Неймана)

. (10.293)

И из формулы (10.288) получаем решение задачи

. (10.294)

Вывод 2. Если на замкнутой поверхности S, являющейся внешней границей области V, среды с материальной характеристикой _а, задано распределение нормальной производной потенциала , а внутри этой поверхности – объемная плотность распределения источников  (V), то решение задачи Неймана для рассматриваемой области дается формулой

, (10.295)

где U(P) – потенциал в произвольной точке Р внутри поверхности S;

G – функция Грина, выражающая потенциал единичного точечного источника, расположенного в точке Р внутри непроницаемой поверхности, совпадающей с S;

N – внешняя нормаль к поверхности S.

Вывод 3. Если на замкнутой поверхности S, являющейся внешней границей области V, среды с материальной характеристикой _а, заданы граничные условия третьего рода , а внутри этой поверхности – объемное распределение источников  (V), то решение задачи Робена дается формулой

, (10.296)

где G – функция Грина, выражающая потенциал единичного точечного источника, расположенного в точке М внутри поверхности S, на которой выполняются граничные условия . Остальные обозначения те же, что и в формуле (10.294).

Вывод 4. Функция Грина G(M, P) имеет вид для трехмерного пространства

. (10.297)

Для плоскости G(M, P) имеет вид

. (10.298)

Функция (М, Р) определяется как решение задачи

ν = 0. (10.299)

В соответствии с формулой (10.296) можно дать физическую интерпретацию функции Грина для первой краевой задачи. Пусть поверхность S, ограничивающая область V, сделана из проводника и заземлена. Поместим в точке Р внутри V положительный электрический заряд величины 1/4_а. Вследствие электростатической индукции на внутренней стороне поверхности возникают отрицательно наведенные заряды плотностью -, а на наружной +. Потенциал электростатического поля в области V будет равен сумме:

а) потенциала поля, созданного точечным зарядом; он равен ;

б) потенциала поля, созданного индуцированными зарядами; он равен ν(М, Р). Эта сумма и равна G(M, P).

Таким образом, G(M, P) можно интерпретировать как потенциал поля, созданного точечным зарядом, помещенным внутри заземленной замкнутой проводящей поверхности. Основная трудность решения методом функции Грина заключается в отыскании функции G. Она найдена лишь для некоторых частных случаев: плоскости, сферы, а также для некоторых комбинаций этих поверхностей. Одним из методов построения функции Грина является метод отражения.

Рассмотрим пример. Найти потенциал в точке М(0, z) на оси эквипотенциального диска радиуса а, расположенного на бесконечной плоскости с нулевым потенциалом, если потенциал диска равен U₀. Расчетная модель к этому примеру приведена на рис. 10.41.

Наша задача – найти функцию Грина с помощью формулы (10.291).

Решение. Функцию Грина ищем методом зеркального отражения. Для этого помещаем в точку М единичный точечный заряд, потенциал диска считаем равным потенциалу бесконечной плоскости, приходим к задаче нахождения поля точечного заряда над проводящей плоскостью.

1. В соответствии с правилами метода отражения в точку М(0, -z₁) поместим фиктивный заряд с обратным знаком. Теперь нужно найти потенциал от обоих зарядов в произвольной точке Р (r, z) верхней полуплоскости. В соответствии с рис. 10.41 для потенциала U(P) можно записать

; (10.300)

.

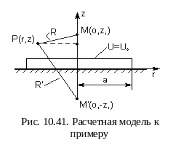
Функция Грина в данном случае легко находится методом отражения

. (10.301)

3. Находим и

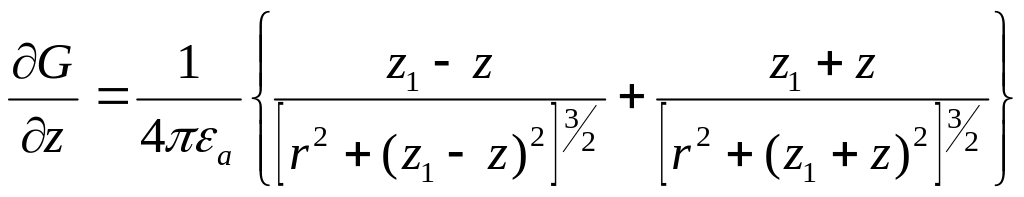(10.302)

.

4. С помощью уравнения (10.292) находим

.

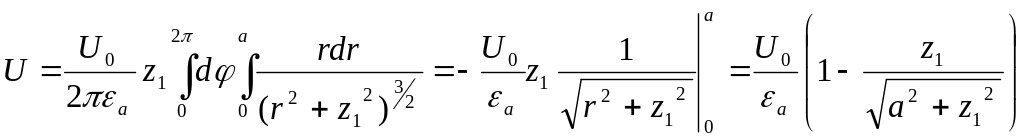Таким образом, решение данной задачи

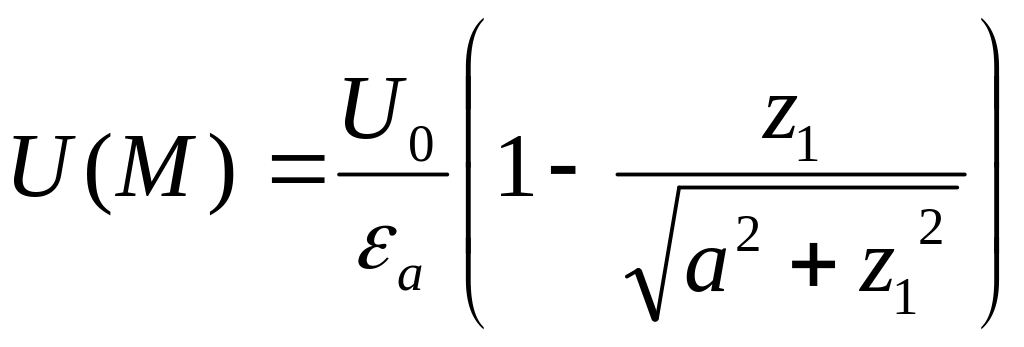. (10.303)