9. Методы, основанные на применении теоремы Гаусса и закона полного тока в интегральной форме

В простых случаях задачи на аналитический расчет электростатических и магнитостатических полей решают путем использования теоремы Гаусса и закона полного тока в интегральной форме. Использование такого искусственного приема позволяет обойтись без интегрирования уравнения Лапласа или Пуассона.

9.1. Применение теоремы Гаусса

Используя теорему Гаусса, легко находить поля, создаваемые симметрично заряженными телами. Рассмотрим, например, шар, если заряд его Q равномерно распределен в шаровой области радиуса r. Среда вне шара однородная и изотропная с диэлектрической проницаемостью ε_а. Требуется рассчитать напряженность электрического поля и потенциал.

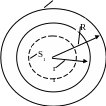
1. Начало сферической системы координат поместим в центре заряженной сферы. Проведем сферическую поверхность S радиусом R>r (рис. 9.36).

S

Рис. 9.36. К расчету поля равномерно заряженного шара

Из соображений симметрии ясно, что поле направлено по радиусам сферы и может зависеть только от расстояния до центра шара.

2. Поскольку задача обладает шаровой симметрией, вектор имеет только одну радиальную проекцию. Для всех точек, равноудаленных от начала координат, модуль D, а следовательно, и E будет иметь одно и то же значение. Поэтому при использовании теоремы Гаусса модуль D выносится из под знака интеграла

. (9.252)

3. Поскольку , где ρ – объемная плотность заряда, а V – объем шара, выражение (9.252) можно записать

. (9.253)

Напряженность электрического поля

. (9.254)

Выражение (9.254) показывает, что вне шаровой области радиуса r, поле является таким же, как и поле точечного заряда Q, расположенного в точке .

Проведем анализ поля внутри заряженной сферы.

1. Проведем сферическую поверхность S₁ с радиусом R < r (см. рис. 9.36). Заряд внутри объема, ограниченного поверхностью S₁, равен , и следовательно, по теореме Гаусса

,

, (9.255)

. (9.256)

2. Потенциал электрического поля при R > r

.

Используя граничные условия φ = 0 при , получаем постоянную интегрирования сonst = 0.

Тогда

. (9.257)

3. При R < r

. (9.258)

Поскольку потенциал непрерывен и однозначен, то на границе сферы, т.е. при R = r (в поле нет поверхностных зарядов)

_, (9.259)

откуда

. (9.260)

В области R < r

. (9.261)

Зависимости φ = φ(R) и E = E(R) приведены на рис. 9.37.

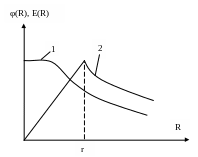
Рис. 9.37. Потенциал (1) и напряженность электрического поля (2) объемного заряда равномерно заряженного шара

9. 2. Применение закона полного тока

При расчете магнитных полей симметричных форм удобно применять закон полного тока в интегральной форме

. (9.262)

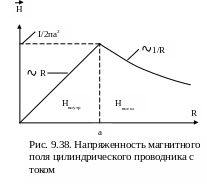
Пример. Пусть по прямому цилиндрическому проводу радиуса а течет постоянный ток I. Требуется найти напряженность поля в произвольной точке, отстоящей на расстоянии R от оси провода.

1. Из симметрии задачи очевидно, что напряженность магнитного поля одинакова во всех точках, равноудаленных от оси, и направлена по касательной к окружности с центром на оси провода. Выбирая в качестве контура L силовую линию магнитного поля, получим для циркуляции вектора

.

Отсюда

. (9.263)

2. В случае, если точка наблюдения находится вне провода, R > a, ΣI_L – полный ток I, текущий по проводнику, а H = H_вн = I/2πR совпадает со значением H для осевого тока. Итак, при R > a

. (264)

3. В случае, если точка наблюдения находится внутри проводника R < a, то ΣI_L представляет собой ток, текущий внутри круга с площадью πR², тогда ΣI_L = δπR² = IR²/a²

(9.265)

где δ – плотность тока, равная отношению I/πa².

4. Для напряженности магнитного поля внутри провода, т.е. при R < a, получим

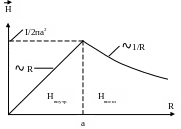
. (9.266)

На рис. 9.38 представлена качественная зависимость напряженности поля от расстояния для рассмотренного примера. Как видно из формул (9.254), (9.256) и рис. 9.38, напряженность магнитного поля, равная нулю на оси провода, внутри проводника растет пропорционально расстоянию R от оси, а во внешнем пространстве убывает обратно пропорционально расстоянию R.

При переходе через поверхность раздела проводник - вакуум напряженность магнитного поля не терпит разрыва непрерывности в соответствии с непрерывностью тангенциального составляющей вектора (H_1t = H_2t).