6. Метод конечных интегральных преобразований (метод г.А.Гринберга)

Метод конечных интегральных преобразований разработан для решения как однородных, так и неоднородных задач по расчету потенциальных полей. Метод применим при тех же условиях, что и метод разделения переменных за исключением ограничения, указанного в разделе 5.4, пункт 4, т.е. метод не требует обязательной однородности граничных условий на ограничивающих анализируемую область координатных поверхностях одного семейства. Кроме того, данный метод применяется при произвольном задании внутри рассматриваемой области сосредоточенных или распределенных источников, т.е. при решении граничных задач не только на уравнение Лапласа, но и на уравнение Пуассона.

6.1. Принцип метода конечных интегральных преобразований

Применение интегральных преобразований позволяет от УЧП с n переменными перейти к новому уравнению с n – I переменными. Интегральные преобразования можно интерпретировать как разложение входного воздействия (на исследуемую область поля) на элементарные (разложение по частотам), нахождение реакции системы на элементарные воздействия и последующее суммирование всех полученных результатов.

Интегральным преобразованием обычно называют преобразование, которое каждой функции f(t) ставит в соответствие новую функцию по формуле

. (6.181)

Видно, что исходная функция зависит от t , а результирующая от S.

Функция K(S,t) называется ядром преобразования. Это основной элемент, отличающий одно преобразование от другого. Обычно ядро выбирают так, чтобы преобразование обладало некоторыми заданными свойствами. Пределы интегрирования также зависят от вида преобразования.

Главное, для чего применяются интегральные преобразования, – это избавление от частных производных по одной из независимых переменных. В преобразованном уравнении будет на одну переменную меньше, чем в исходном. Например, если применить интегральное преобразование к уравнению U_t=U_xx, чтобы избавиться от производной по t, получим ОДУ с независимой переменной x. Если к уравнению дважды применить интегральное преобразование по переменной x , то производная U_xx будет исключена, а в новом уравнении останется только две независимые переменные y и z. Исключая таким же образом еще одну переменную, получим ОДУ с одной оставшейся независимой переменной. Как видно, интегральные преобразования упрощают исходную задачу. После их применения решается преобразованная, более простая задача, а применяя к ее решению обратное преобразование, получают решение исходной задачи. Естественно, что с каждым прямым интегральным преобразованием связано обратное преобразование, которое восстанавливает первоначальную функцию из преобразованной. Прямое и обратное преобразования принято называть парой преобразований.

6. 2. Собственные значения и собственные функции краевой задачи

Рассматриваемый метод базируется на использовании аппарата так называемых собственных функций, определение и основные свойства которых мы рассмотрим на простейшем примере использования метода разделения переменных.

Рис. 6.24. Простейшая расчетная модель к

b примеру расчета поля методом разделения

переменных

U=0 U=o

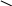U=0 a

Пример. Пусть требуется найти распределение потенциала для расчетной модели, представленной на рис. 6.24. Идея метода разделения переменных подробно рассматривалась в разделе 5, поэтому решение приводим без подробных разъяснений.

Решение

1. Искомое распределение потенциала удовлетворяет двумерному уравнению Лапласа

. (6.182)

2. Частные решения уравнения (6.182) ищем в виде

. (6.183)

3. Подставляя из (6.183) в уравнение Лапласа (6.182), получим

. (6.184)

4. Обе части уравнения (6.184) делим на произведение X(x)Y(y):

. (6.185)

5. Равенство (6.185) возможно только тогда, когда

, , (6.186)

где – постоянное число, постоянная разделения.

В результате относительно функции X(x) и Y(y) получаем следующие ОДУ:

. (6.187)

6. Записываем общее решение ОДУ для X(x):

. (6.188)

7. Определим коэффициенты и из граничных условий задачи X(0)=0 , X(a)=0:

а) =0, (6.189)

б) ; . (6.190)

Поскольку , иначе было бы, что X(x)=0, и потенциал во всей рассматриваемой области оказался бы равным нулю, то , т.е. , где p=1,2,… (значение p=0 отбрасывается, так как при в общем решении для X(x) для выполнения граничных условий X(x)=X(a)=0 следует положить ).

Таким образом, видно, что нетривиальное (ненулевое) решение существует не при всех, а лишь при вполне определенных значениях p.

Определение. Те значения , при которых задача имеет нетривиальные решения, называются собственными значениями (СЗ), а соответствующие им самим решения – собственными функциями (СФ) краевой задачи.

В данном случае решение при p=1,2,…

(6.191)

является собственными функциями данной краевой задачи.

Важным свойством собственных функций является то, что задача их определения может быть решена лишь при однородных условиях на границах интервала изменения в рассматриваемой области хотя бы одной координаты (в нашем случае x).

8. Общее решение для функции Y(y) запишется следующим образом:

, (6.192)

где коэффициенты и зависят от p.

9. Для нахождения используем граничные условия Y(0)=0, получим =0, т.е.

. (6.193)

10. Частные решения рассматриваемой задачи имеют вид

. (6.194)

Дальнейшие рассуждения и математические выкладки, необходимые для решения задачи, не отличаются от приведенных в разделе 5.1 формул (5.49) - (5.58). С учетом различия в граничных условиях расчетных моделей (рис.5.10 и рис. 6.24) окончательное решение данной задачи принимает вид

, (6.195)

где . (6.196)