
- •4. Методы, наиболее часто применяемые на практике при решении
- •5. Метод Фурье решения краевых задач
- •9. Методы, основанные на применении теоремы Гаусса и
- •1.1. Постановка задач по расчету потенциальных полей
- •1. 2. Элементы теории уравнений с частными производными
- •1. 3. Дифференциальное уравнение
- •1.4. Типы уравнений с частными производными
- •1. 5. Решение уравнений с частными производными
- •2. Математическая аналогия между потенциальными полями
- •3. Общие свойства уравнения Лапласа
- •3.1. Классификация уравнения
- •3. 2. Физический смысл оператора Лапласа
- •3.3. Особенности решения
- •3.4. Граничные условия
- •3.5. Выбор системы координат при решении уравнений Лапласа и Пуассона
- •Декартовы прямоугольные координаты
- •Цилиндрические координаты
- •Сферические координаты
- •3.6. Единственность решения уравнения Лапласа. Принцип композиции
- •3.7. Расчетные модели и основные принципы их построения
- •4. Методы, наиболее часто применяемые на практике при решении уравнений с частными производными
- •4.1. Классификация методов решения уравнений с частными производными
- •4.2. Схема расчета потенциальных полей
- •5. Метод Фурье решения краевых задач (метод разделения переменных)
- •5.1. Решение уравнения Лапласа в прямоугольной системе координат методом разделения переменных
- •5.2. Решение уравнения Лапласа в цилиндрической системе координат
- •5.3. Решение уравнения Лапласа в сферической системе координат
- •5.4. Краткая характеристика метода разделения переменных
- •6. Метод конечных интегральных преобразований (метод г.А.Гринберга)
- •6.1. Принцип метода конечных интегральных преобразований
- •6. 2. Собственные значения и собственные функции краевой задачи
- •6.3. Простейший пример использования метода конечных интегральных преобразований
- •7. Метод зеркальных изображений
- •7.1. Принцип метода
- •7. 2. Общий случай расчета электростатического поля вблизи плоской границы двух сред
- •7. 3. Применение метода зеркальных изображений для расчета магнитных полей, создаваемых токами, протекающими вблизи ферромагнитных масс
- •8. Метод наложения
- •9. Методы, основанные на применении теоремы Гаусса и закона полного тока в интегральной форме
- •9.1. Применение теоремы Гаусса
- •9. 2. Применение закона полного тока
- •10. Метод функции Грина решения краевых задач для уравнений эллиптического типа
- •10.1. Формулы Грина
- •1.Формулы Грина выводят из теоремы Остроградского – Гаусса:
- •10. 2. Применение аппарата δ - функций в электродинамике
- •10. 3. Сущность метода функций Грина
- •11. Метод интегральных уравнений
- •12. Решение уравнений с частными производными методом конформных отображений
- •12.1. Понятие функции комплексного переменного
- •12. 2. Определение конформного отображения
- •13. Численное решение уравнений с частными производными
- •13.1. Основные понятия метода сеток
- •13. 2. Метод сеток для задачи Дирихле
- •Библиографический список
- •620062, Екатеринбург, ул. Мира, 19
5.2. Решение уравнения Лапласа в цилиндрической системе координат
1. Уравнение Лапласа в цилиндрической системе координат (r,φ,z):
![]() . (5.59)
. (5.59)
2. Ищем частное решение
этого уравнения
![]() в
виде произведения трёх функций
в
виде произведения трёх функций
![]() . (5.60)
. (5.60)
3. Подставляем (5.60) в исходное уравнение (5.59):
![]() . (5.61)
. (5.61)
4. Обе части уравнения
(5.61) делим на произведение
![]() :
:
![]() . (5.62)
. (5.62)
5. Равенство (5.62) может соблюдаться только в том случае, если
![]() ,
,
![]() , (5.63)
, (5.63)
другими словами, для соблюдения равенства нулю левой части уравнения (5.62) необходимо положить
![]() ,
,
![]() , (5.64)
, (5.64)
где k
и m– произвольные
постоянные числа. Выбор знака у
![]() и
и
![]() не носит принципиального значения.
Выбрав знак таким образом, мы сразу
предполагаем, что решение для Ф будет
выражено в обычных тригонометрических
функциях, а для Z – в
гиперболических функциях. Уравнение
для Z и Ф (5.64) – обыкновенное
дифференциальное уравнение второго
порядка.
не носит принципиального значения.
Выбрав знак таким образом, мы сразу
предполагаем, что решение для Ф будет
выражено в обычных тригонометрических
функциях, а для Z – в
гиперболических функциях. Уравнение
для Z и Ф (5.64) – обыкновенное
дифференциальное уравнение второго
порядка.
![]() ,
,
![]() . (5.65)
. (5.65)
По аналогии с (5.35) и
(5.36) решение для
![]() запишется
запишется
![]() , (5.66)
, (5.66)
а для
![]() по аналогии с (5.37) и (5.41) решение запишется
так:
по аналогии с (5.37) и (5.41) решение запишется
так:
![]() . (5.67)
. (5.67)
6. Вернёмся к уравнению (5.62). С учётом принятых в (5.64) обозначений его можно записать так:
![]() (5.68)
(5.68)
а) умножим обе части этого уравнения на R, получим
![]() , (5.69)
, (5.69)
б) в
левой части уравнения (5.69) выполним
дифференцирование
![]() по правилам дифференцирования произведения
двух функций
по правилам дифференцирования произведения
двух функций
![]() .
.
Тогда уравнение (5.69) в результате будет иметь вид
![]() (5.70)
(5.70)
Комментарии к уравнению (5.70):
Уравнение (5.70) является дифференциальным уравнением второго порядка с переменными коэффициентами, поэтому его решение не выражается через обычные элементарные функции, а приводит к так называемым специальным функциям – функциям Бесселя m- го порядка.
Смысл выражения «функция Бесселя m- го порядка» заключается в том, что для различных значений m решением уравнения будут являться различные функции, т.е. разные значения m определяют собой разные дифференциальные уравнения и, следовательно, различные по характеру решения.
Величина k при заданном значении m не меняет характера уравнения.
Уравнение (5.70) может быть легко приведено к «классическому» виду уравнения Бесселя, для этого
а) все члены уравнения (5.70) делим на :
![]() ;
;
б)
введём новую независимую переменную
![]() ,
тогда
,
тогда
![]() ,
,
![]() ,
,
![]() .
.
Составляющие уравнения (5.70) в новой переменной:
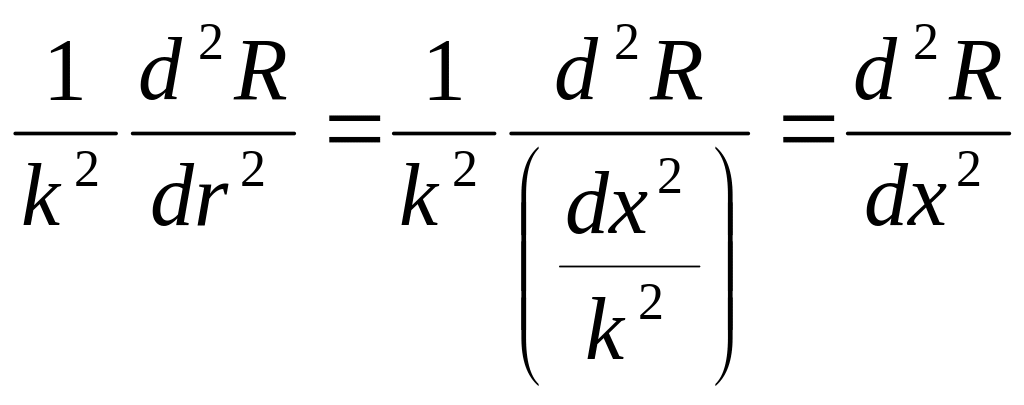 ;
;
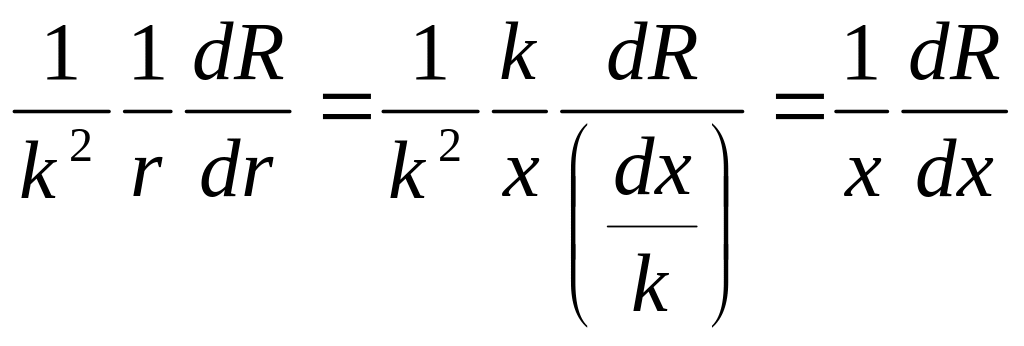 ;
;
![]() .
.
Классический вид уравнения Бесселя
![]() ,
(5.71)
,
(5.71)
именно в таком виде оно обсуждается в специальных разделах курса высшей математики, приводится в справочной литературе;
в) таким образом, при решении уравнения
Лапласа в цилиндрической системе
координат методом Фурье или методом
разделения переменных с помощью
подстановки
мы определили
,
,
а для нахождения
![]() необходимо решить уравнение Бесселя
(5.70) или (5.71). Прежде чем выяснить, как
это сделать, обсудим смысл постоянной
m.
необходимо решить уравнение Бесселя
(5.70) или (5.71). Прежде чем выяснить, как
это сделать, обсудим смысл постоянной
m.
Постоянная величина m
входит в уравнение Бесселя и определяет
закон изменения поля вдоль радиуса r.
Кроме того, входя в решение
,
m определяет зависимость
потенциала от угла
![]() .
Из уравнения (5.66):
следует, что m может
быть только целым числом. Действительно,
если рассуждать от обратного и считать
m дробным числом, то
.
Из уравнения (5.66):
следует, что m может
быть только целым числом. Действительно,
если рассуждать от обратного и считать
m дробным числом, то
![]() ,
а
,
а
![]() ,
что в таком случае свидетельствует о
многозначной зависимости потенциала
от угла
,
а это физически не реализуется, т.е.
неверно. Итак, m –
целое число.
,
что в таком случае свидетельствует о
многозначной зависимости потенциала
от угла
,
а это физически не реализуется, т.е.
неверно. Итак, m –
целое число.
7. Решение дифференциального уравнения Бесселя.
Для любого фиксированного m уравнение Бесселя является дифференциальным уравнением второго порядка. Как и всякое линейное дифференциальное уравнение, содержащее в качестве наивысшей производной вторую производную, это уравнение имеет два независимых частных решения.
Первое частное решение уравнения Бесселя
называют функцией Бесселя m
- го порядка или цилиндрической функцией
первого рода. Эта функция обозначается
![]() .
.
Второе частное решение называют
цилиндрической функцией m-
го порядка второго рода или функцией
Неймана. Её обозначают
![]() .
.
Общее решение уравнения Бесселя имеет вид
![]() , (5.72)
, (5.72)
где с1 и с2 – произвольные постоянные, определяемые из граничных условий.
Функции Бесселя и Неймана имеют широкое применение в различных областях техники и, в частности, в радиотехнике, электронике, электротехнике. Эти функции табулированы, для них имеются графические зависимости численных значений функции для различных целых значений индексов m от аргумента x. Если известны x и m, то по графикам находятся числа, соответствующие и .
Для
m=0,
![]() может быть вычислена по формуле
может быть вычислена по формуле
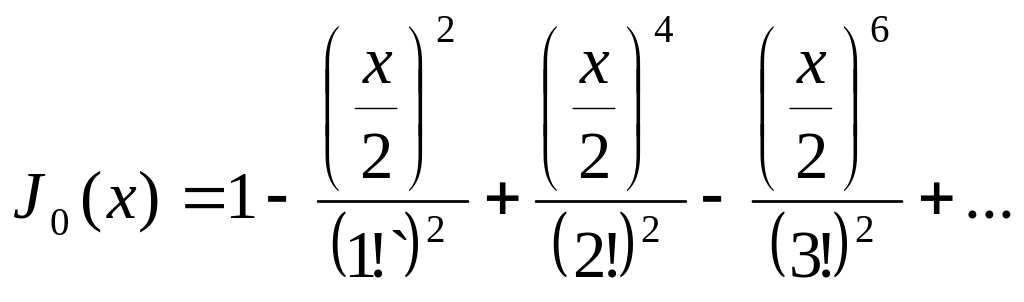 (5.73)
(5.73)
Для
m=1,
![]() рассчитывается
так:
рассчитывается
так:
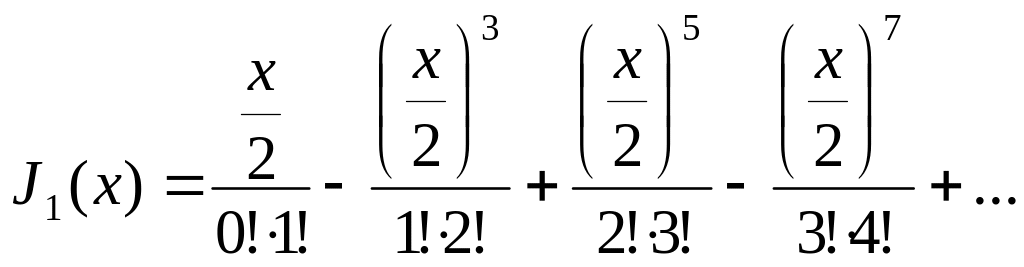 (5.74)
(5.74)
Для произвольного m, рассчитывают по формуле
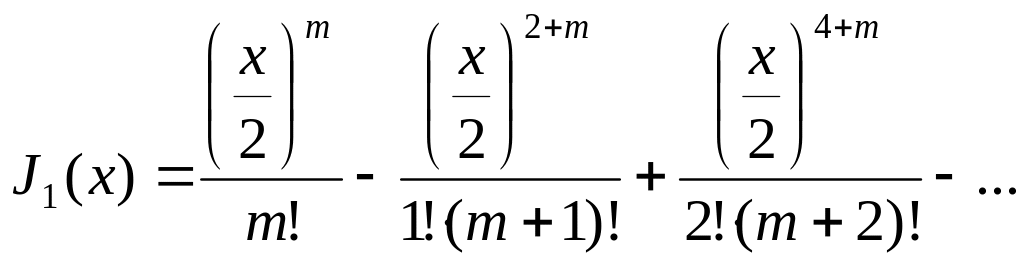 (5.75)
(5.75)
Функции Неймана любого целого порядка m можно представить через функции Бесселя:
![]() . (5.76)
. (5.76)
Ряд простейших свойств функций Бесселя и Неймана, которые полезно запомнить:
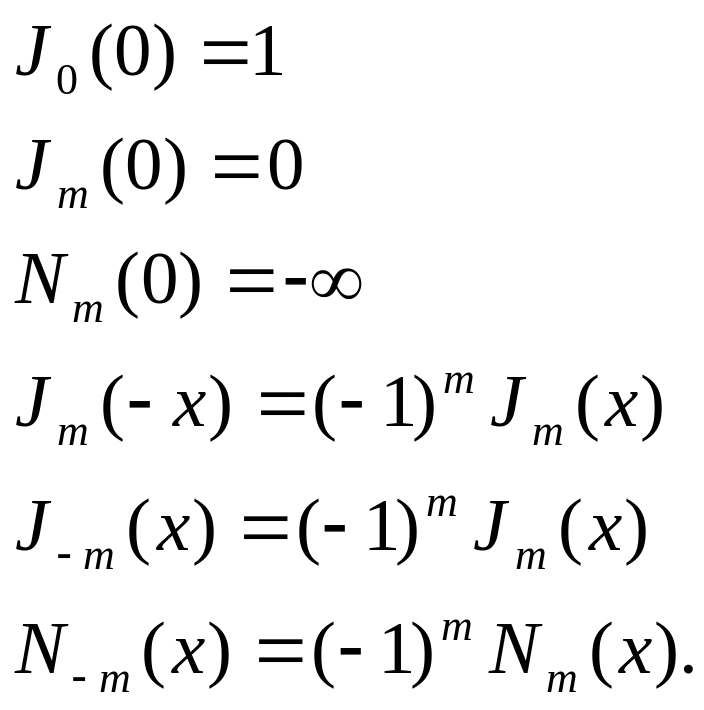 (5.77)
(5.77)
При
решении задач анализа физических полей
часто бывает необходимым знать значения
корней Бесселевых функций, т.е. те
значения x,
которые обращают в нуль функцию. Корни
обозначаются символом
![]() ,
где m
– порядок функции Бесселя, n
–
номер корня.
Корни функций Бесселя и Неймана в
справочной литературе приведены в виде
таблиц и графиков.
,
где m
– порядок функции Бесселя, n
–
номер корня.
Корни функций Бесселя и Неймана в
справочной литературе приведены в виде
таблиц и графиков.
Практически важным свойством функции Бесселя является то, что любую функцию кусочно-гладкую на интервале от 0 до а можно представить в виде ряда Бесселевых функций
![]() .
(5.78)
.
(5.78)
Этот ряд называется рядом Фурье-Бесселя.
8. Таким образом, решая уравнение Лапласа в цилиндрической системе координат, приходим к следующим частным решениям для функции Ф(φ), Z(z), R(r):
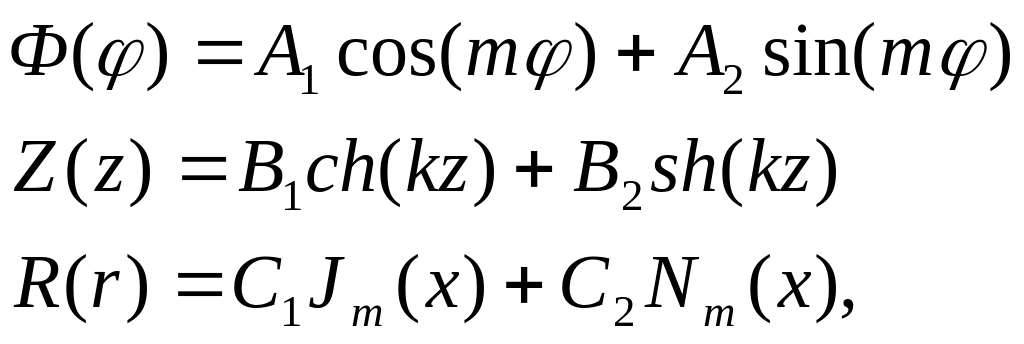 (5.79)
(5.79)
где x=kr.
Тогда
частное решение
![]() в соответствии с основными идеями метода
Фурье запишется
в соответствии с основными идеями метода
Фурье запишется
![]() (5.80)
(5.80)
Рассмотрим конкретный пример, иллюстрирующий применение результатов решения уравнения Лапласа в цилиндрической системе координат.
Дано:
круглый металлический заземленный
цилиндр с радиусом а,
верхняя
крышка цилиндра изолирована и имеет
потенциал
![]() .
.
Требуется найти распределение потенциала внутри цилиндра (рис. 5.12).
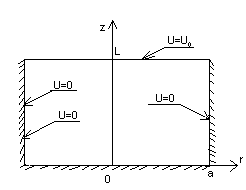
Рис. 5.12. Круглый металлический заземленный цилиндр радиусом а
и высотой L
Решение
1. По типу граничных условий данная задача – типичная краевая задача с граничными условиями первого рода (задача Дирихле). Требуется найти решение уравнения Лапласа внутри цилиндра, на границе указанной области решение должно принять заданные значения U=0 и .
2. Очевидно, что граничные условия поставленной задачи будут иметь более простой вид в цилиндрической системе координат (рис. 5.12):
z=0, U=0,
r=a, U=0,
z=L,
3.
Анализ симметрии задачи при выбранной
системе координат показывает, что
потенциал не зависит от угла φ, т.е. в
решении уравнения Лапласа в цилиндрической
системе координат (5.79) функция
Ф(φ)![]() f(φ)=const,
а это возможно только при m=0.
f(φ)=const,
а это возможно только при m=0.
Действительно, тогда
Ф(φ)=![]() .
(5.81)
.
(5.81)
Таким
образом, после учета симметрии задачи
частное решение
![]() .
Следовательно, в соответствии с (5.80) оно
будет иметь вид
.
Следовательно, в соответствии с (5.80) оно
будет иметь вид
![]() .
(5.82)
.
(5.82)
Выражение (5.82) составлено уже с учетом m=0 и x=kr.
4.
Искомый потенциал должен иметь конечное
значение во всех точках внутри цилиндра,
в том числе и на оси цилиндра, при r=0.
Однако, как следует из (5.77), функция
Неймана не остается конечной при нулевом
значении аргумента. Поэтому из физических
соображений конечности потенциала во
всех точках исследуемого пространства
необходимо в решении (5.82) принять
![]() .
После этого этапа частное решение
.
После этого этапа частное решение
![]() примет следующий вид:
примет следующий вид:
![]() .
(5.83)
.
(5.83)
5. Дальнейшее определение входящих в решение констант связано с использованием граничных условий:
а) первое граничное условие z=0, U=0. Следовательно:
![]() .
.
![]() .
(5.84)
.
(5.84)
Равенство (5.84) возможно при любом значении r, если . После удовлетворения первого условия частное решение примет вид
![]() (5.85)
(5.85)
б) второе граничное условие r=a, U=0. Следовательно:
![]() .
(5.86)
.
(5.86)
Для выполнения этого условия при любом z необходимо, чтобы
![]() .
(5.87)
.
(5.87)
Из (5.87) следует, что произведение ak должно быть равным одному из корней бесселевой функции нулевого порядка.
Итак,
![]() где
где
![]() –
это p-й
корень (номер корня) функции Бесселя
нулевого порядка от аргумента ak
. Тогда
–
это p-й
корень (номер корня) функции Бесселя
нулевого порядка от аргумента ak
. Тогда
![]() .
(5.88)
.
(5.88)
Частное решение после нахождения k примет вид
![]() ,
(5.89)
,
(5.89)
в)
третье граничное условие z=L,
U=![]() .
.
![]() .
(5.90)
.
(5.90)
В
этом уравнение сомножитель
![]() –
это число, которое можно обозначить
сonst,
тогда предполагаемое равенство (5.90)
можно переписать в виде
–
это число, которое можно обозначить
сonst,
тогда предполагаемое равенство (5.90)
можно переписать в виде
![]() .
(5.91)
.
(5.91)
Из
выражения (5.91) видно, что это равенство
не может быть справедливым ни при каком
значение p,
т.е. полученная функция потенциала
![]() не остается постоянной вдоль крышки
цилиндра при z=L,
как этого требует третье граничное
условие, а изменяется по закону функции
Бесселя.
не остается постоянной вдоль крышки
цилиндра при z=L,
как этого требует третье граничное
условие, а изменяется по закону функции
Бесселя.
Придавая p разные значения p=1,2,3…, можно построить распределения потенциала вдоль радиуса цилиндра, даваемое частным решением (5.89), и убедиться с помощью этого решения в невозможности достижения требуемого распределения потенциала при z=l (рис.5.13).
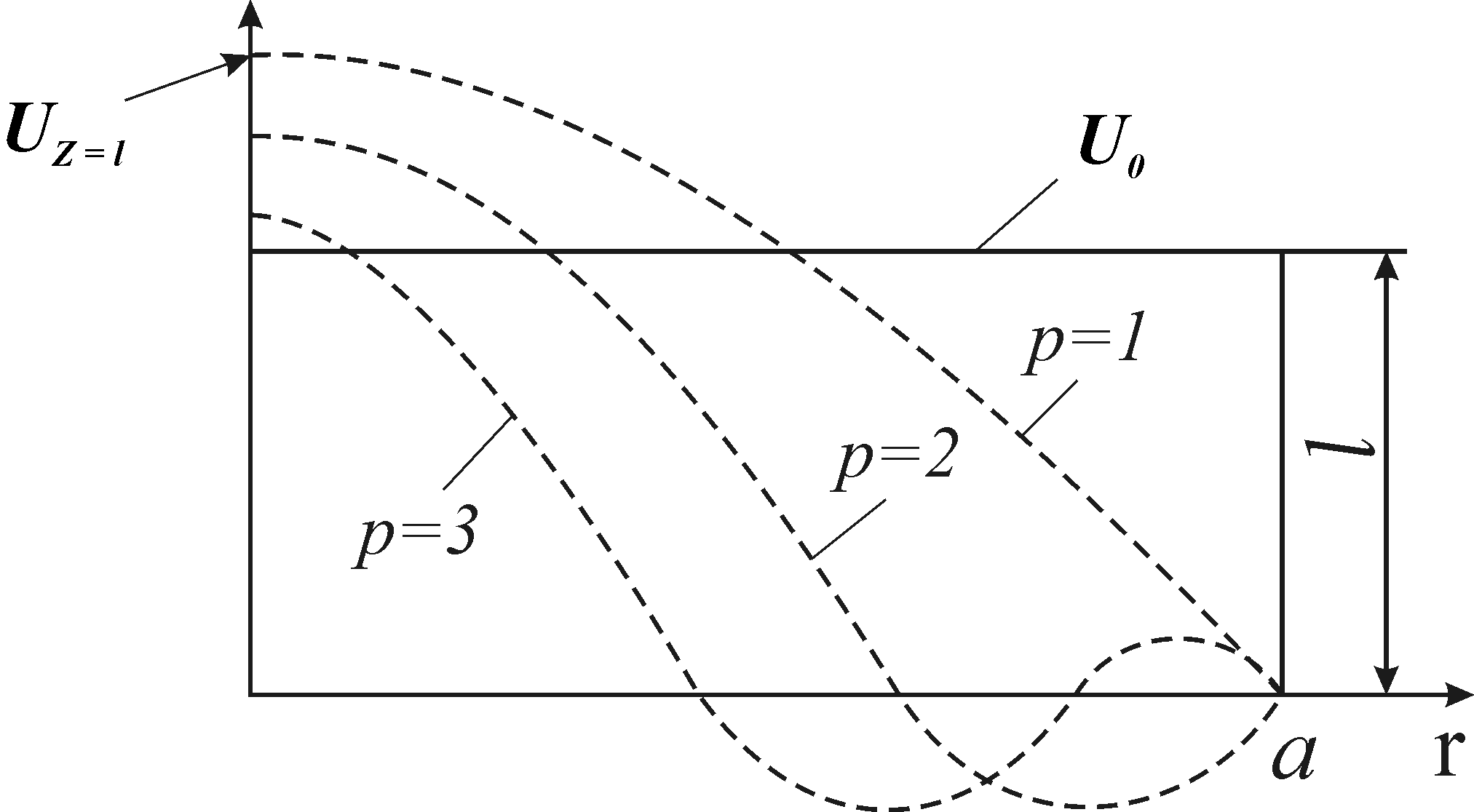
Рис. 5.13. Распределения потенциала вдоль радиуса цилиндра при z=l:
– требуемое распределение; пунктир – распределение при p=1,2,3
в соответствии с решением уравнения 5.89
На
этом рисунке требуемым распределением
потенциала при z=l
является
![]() .
.
6. Поскольку ни при каких значениях p не удается удовлетворить третьему граничному условию, используем принцип суперпозиции – сумма частных решений будет также решением.
![]() .
(5.92)
.
(5.92)
7. Снова попытаемся удовлетворить третьему граничному условию при z=l, .
![]() .
(5.93)
.
(5.93)
Кроме того, в соответствии с (5.78) разложим функцию U(r,L) в ряд Фурье-Бесселя:
![]() .
(5.94)
.
(5.94)
Составляя равенство на основании (5.93) и (5.94), получим
![]() .
.
Приходим к заключению, что
![]() .
(5.95)
.
(5.95)
Отсюда
видно, что для нахождения
![]() необходимо найти
.
необходимо найти
.
8. Для нахождения воспользуемся уравнением (5.78). Зафиксируем число p, приравняв его к произвольному числу, например k. Тогда
![]() .
(5.96)
.
(5.96)
Равенство
(5.96) умножим на функцию
![]() :
:
![]() (5.97)
(5.97)
и проинтегрируем в пределах от 0 до а:
![]() .
(5.98)
.
(5.98)
Тогда
постоянный коэффициент
![]() будет определяться выражением
будет определяться выражением
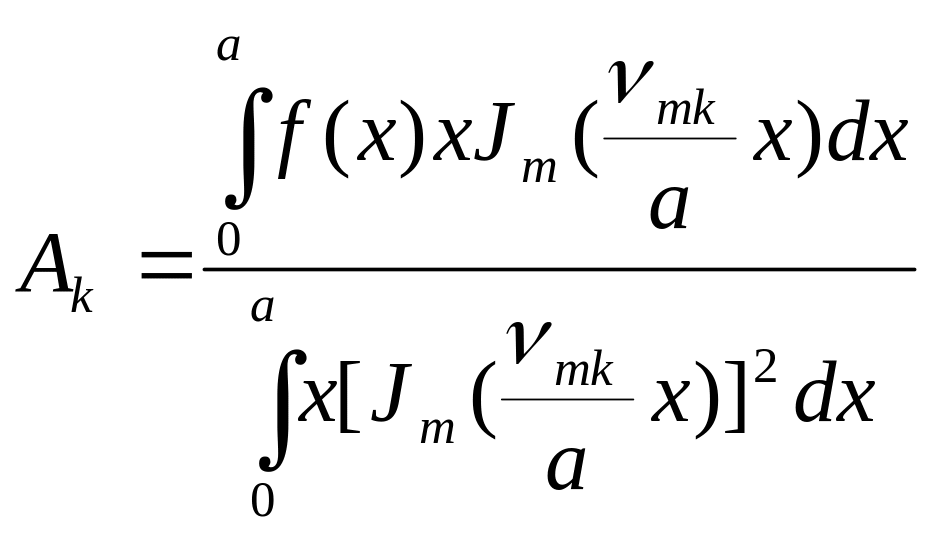 .
(5.99)
.
(5.99)
В условиях данной конкретной задачи f(x)=U(r,l)= , x=r, m=0, равенство (5.99) упростится до вида
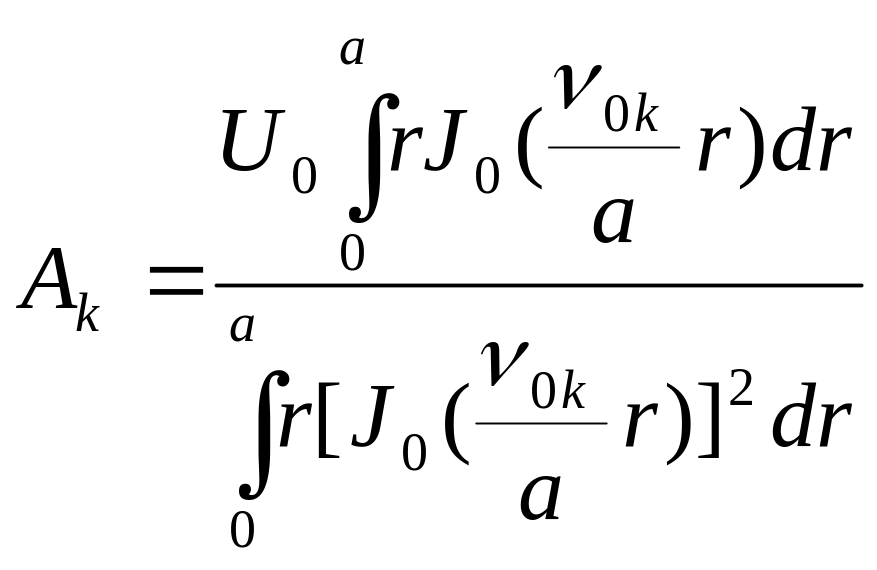 .
(5.100)
.
(5.100)
Теперь для нахождения нужно вычислить два интеграла
![]() и
и
![]() .
.
Для вычисления этих интегралов необходимо обратиться к специальной литературе.
Первый интеграл в (100)
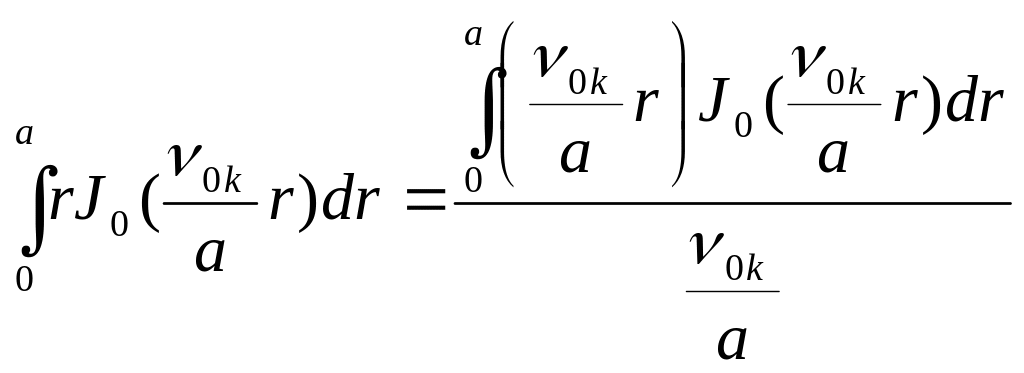 .
(5.101)
.
(5.101)
Введем новую переменную
![]() ,
(5.102)
,
(5.102)
тогда
![]() ,
следовательно
,
следовательно
![]() .
(5.103)
.
(5.103)
В новой переменной интеграл (5.101) запишется
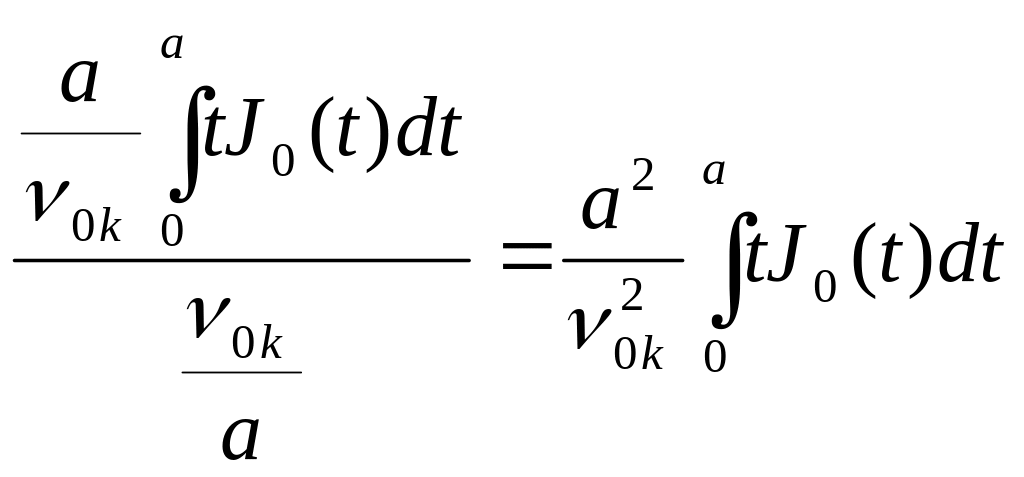 .
(5.104)
.
(5.104)
Интеграл
![]() – табличный вида
– табличный вида
![]() (5.105)
(5.105)
При m=1 (как это следует из (5.104) и (5.105))
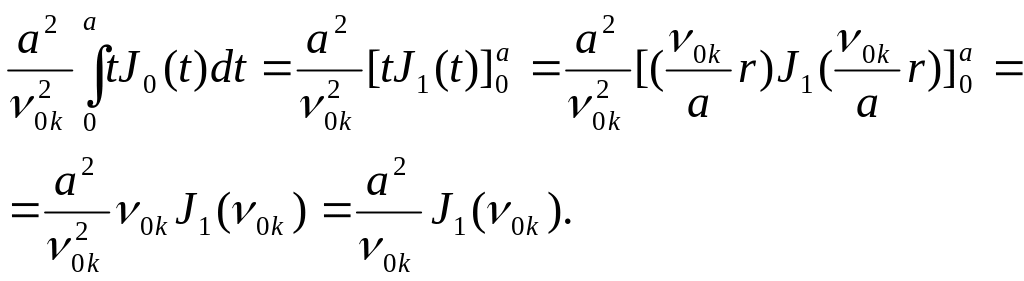 (5.106)
(5.106)
Второй интеграл в (5.100) по аналогии с (5.106) может быть приведен к виду
![]() ,
(5.107)
,
(5.107)
где
интеграл
![]() – табличный вида
– табличный вида
![]() .
(5.108)
.
(5.108)
При m=0 (как это следует из (5.107) и (5.108))
![]() .
(5.109)
.
(5.109)
Учитывая,
что
![]() при m=1
преобразуется к виду
при m=1
преобразуется к виду
![]() ,
выражение (5.109) можно представить
следующим образом:
,
выражение (5.109) можно представить
следующим образом:
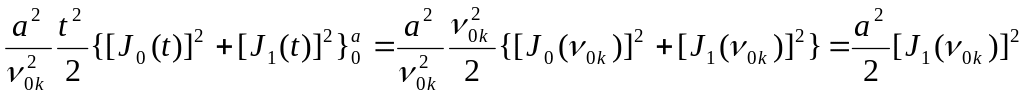 .
(5.110)
.
(5.110)
С учетом (5.106) и (5.110) для можно записать
![]() .
(5.111)
.
(5.111)
Таким образом, для удовлетворения последнего граничного условия коэффициент должен быть
. (5.112)
После
этого из (5.95) находим
![]() :
:
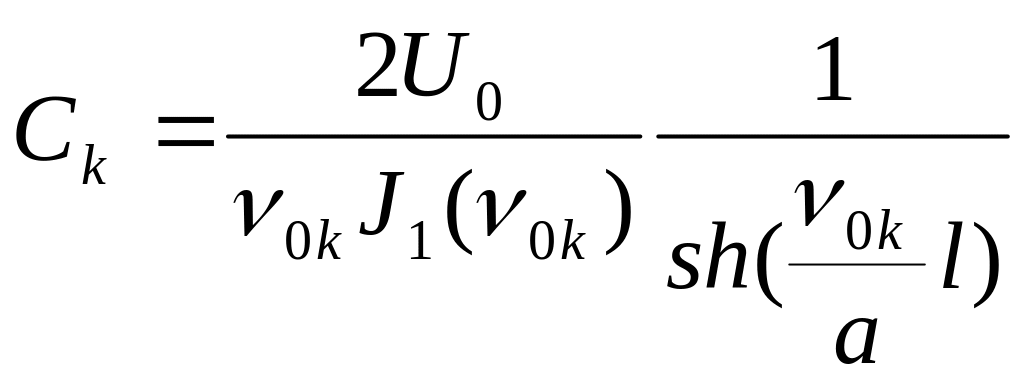 .
(5.113)
.
(5.113)
Возвращаясь снова к индексу и подставляя найденные значения в разложение (5.92), получаем окончательное решение задачи:
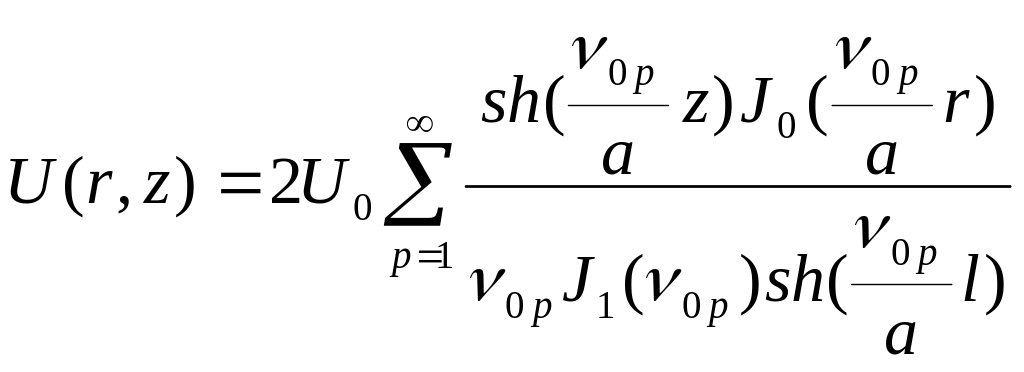 .
(5.114)
.
(5.114)
