5.6. Рівняння динаміки однофазних трансформаторів
Розглянемо рівняння динаміки однофазного трансформатора, який працює на активно-індуктивне навантаження через ємнісний фільтр.
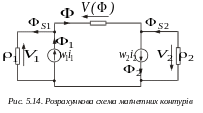
На рис. 5.11 наведена принципова схема трансформатора з навантаженням, на рис. 5.12, 5.13 – розрахункові схеми електричних контурів, на рис. 5.14 – розрахункова схема маґнетного кола.
З
гідно
законів Кірхгофа запишемо рівняння
електричних контурів
,
,
(5.89)
,
,
(5.90)
.
(5.91)
Е.р.с.
,
визначаються за формулами
,
,
(5.92)
Підставимо (5.92) в (5.89)
,
.
(5.93)
Визначимо з (5.90) струм конденсатора і підставимо в (5.91)
.
(5.94)
Згідно (5.66) визначимо напругу на індуктивності навантаження
.
(5.95)
В
рівняннях (5.93) - (5.95) використані наступні
позначення:
– опір, індуктивність і струм навантаження;
– ємність і напруга конденсатора;
– числа витків обмоток;
– струми обмоток;
– напруга живлення;
– активні опори обмоток;
– маґнетні потоки обмоток.
Згідно схеми рис. 5.14 можна записати рівняння стану маґнетного кола
,
,
(5.96)
,
,
(5.97)
,
,
(5.98)
,
(5.99)
де
– маґнетні потоки розсіяння обмоток;
– основний маґнетний потік;
– падіння маґнетної напруги в осерді
трансформатора;
– маґнетні опори розсіяння обмоток.
Підставивши (5.97) в (5.98) визначимо потоки розсіяння
(5.100)
Підставимо (5.100) в (5.96) і визначимо струми обмоток
(5.101)
Підставимо (5.101) в (5.93), (5.94), (5.99)
,
,
(5.102)
,
(5.103)
,
(5.104)
де
,
.
Рівняння (5.80)
нелінійне за рахунок функції
,
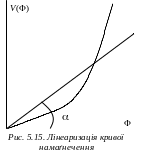
яка є кривою намаґнечення. Її характер
зображений на рис. 5.15. Для того, щоб
рівняння (5.80) було лінійним замінимо
криву
рівнянням прямої, що проходить через
початок координат
,
.
(5.105)
Підставимо (5.105) в (5.104) і визначимо основний маґнетний потік
,
,
.
(5.106)
де
.
Підставимо (5.106)
в (5.102),
(5.103),
(5.95)
,
(5.107)
,
(5.108)
,
(5.109)
. (5.110)
Згідно
схеми рис. 5.11 вхідною величиною є напруга
,
а вихідною напруга на навантаженні.
Остання співпадає з напругою конденсатора
.
Тому в системі рівнянь (5.107)
-
(5.110)
необхідно виключити проміжні змінні
.
В результаті ми отримаємо одне рівняння
четвертого порядку відносно
.
Визначимо
з (5.107)
і підставимо в (5.108),
(5.109)
,
(5.111)
,
(5.112)
де
,
,
,
,
,
,
,
.
З рівняння (5.112) визначимо і підставимо в (5.110)
.
(5.113)
Знайдемо зображення за Лапласом рівнянь (5.112), (5.113)
(5.114)
(5.115)
З
рівняння (5.114)
визначимо
,
а отриманий результат підставимо в
(5.115)
,
(5.116)
де
,
,
,
,
,
,
,
,
.
Тоді передатна функція згідно (5.116) буде
.
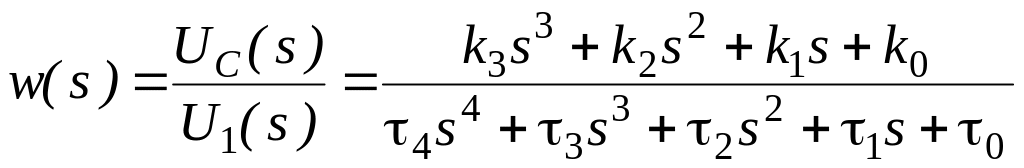(5.117)