5.4. Форсуючий rc-фільтр

С хема диференціюючого RC-контуру, що забезпечує додавання сигналу помилки з похідною цього сигналу, зображена на рис. 5.8. Цей контур може безпосередньо включатися в коло передачі сигналу помилки. Цей контур інколи називають форсуючим. Вважаючи еквівалентним опором, що враховує вплив навантаження, згідно другого закону Кірхгофа маємо:

. (5.45)

Згідно першого закону Кірхгофа струми пов’язані рівнянням

. (5.46)

Рівняння елементів схеми мають вигляд

. (5.47)

Розв’язуючи систему рівнянь (5.45) – (5.47) відносно отримаємо

, (5.48)

де .

Так як , це приводить до ослаблення сигналу, тому форсуючий контур вимагає введення послідовного підсилювача.

Рівняння динаміки у формах абсолютних і відносних приростів для форсуючого контуру у відповідності з (5.48) мають вигляд:

, (5.49)

, (5.50)

де .

Визначимо передатну функцію такого фільтру. Зображення за Лапласом рівняння (5.50) має вигляд

, (5.51)

Передатна функція згідно (5.51) буде

. (5.52)

Підставивши отримаємо вираз для АФХ об’єкту

. (5.53)

Цей запис є тотожним виразу (2.71), де

(5.54)

Тоді частотні характеристики об’єкту за вхідною дією будуть визначатися виразами (2.74) – (2.77) з урахуванням позначень (5.54).

5.4. Інтегруючий rc-фільтр

В цьому фільтрі на відміну від диференціюючого постійний сигнал проходить, бо вихідною є напруга на конденсаторі. Зауважимо, що інтегруючим він буде по відношенню до змінних сигналів, а по відношенню до постійних він виконує функцію повторювача.

Н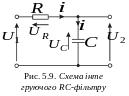 а рис. 5.9 зображена диференціююча RC-ланка. Згідно другого закону Кірхгофа для електричних контурів маємо

, , (5.55)

де – падіння напруги на конденсаторі; – падіння напруги на активному опорі; – вхідна і вихідна напруги.

Рівняння елементів фільра мають вигляд

, . (5.56)

Розв’язуючи систему рівнянь (5.55), (5.56) відносно , отримаємо

, . (5.57)

Рівняння (5.57) лінійне, тоді запишемо його в абсолютних та відносних приростах

, (5.58)

, (5.59)

де , , .

Визначимо передатну функцію інтегруючого фільтру. Зображення за Лапласом рівняння (5.59) має вигляд

, (5.60)

Передатна функція згідно (5.60) буде

. (5.61)

Підставивши отримаємо вираз для АФХ об’єкту

. (5.62)

Цей запис є тотожним виразу (2.71), де

(5.63)

Тоді частотні характеристики об’єкту за вхідною дією будуть визначатися виразами (2.74) – (2.77) з урахуванням позначень (5.63).

5.5. RLC-фільтр четвертого порядку

Н аведена на рис. 5.10 -ланка складається з двох дроселів з опорами та індуктивностями , та двох конденса­торів . Індуктивності дроселів будемо вважати постійними. Ланка наван­тажена активним опором і живиться напругою . Для запису рівнянь динаміки скористаємось законами Кірхгофа та рівняннями елементів.

Дана схема містить три вузли і для двох з них запишемо рівняння І-го закону Кірхгофа

(5.64)

де – струми дроселів; – струми конденсаторів; – струм навантаження.

Маємо чотири незалежних контури для яких запишемо рівняння ІІ-го закону Кірхгофа

(5.65)

(5.66)

(5.67)

(5.68)

де – напруги конденсаторів; – напруги на активних опорах котушок; – напруги на індуктивних опорах котушок; – напруга навантаження; – напруга на виході ланки.

Рівняння Кірхгофа доповнимо рівняннями елементів

(5.69)

Підставимо рівняння (5.69) в (5.64)-(5.68)

(5.70)

(5.71)

(5.72)

(5.73)

(5.74)

(5.75)

З рівнянь (5.70), (5.74), (5.75) визначимо змінні та підставимо їх у рівняння (5.71) – (5.73)

(5.76)

(5.77)

(5.78)

Вираз (5.76) для струму другого дроселя підставимо в (5.77), (5.78)

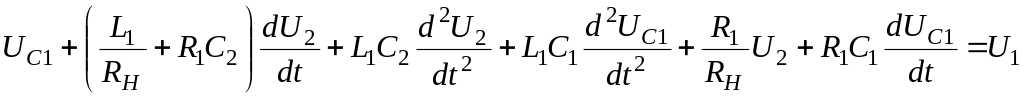, (5.79)

(5.80)

Підставивши вираз (5.80) для напруги в рівняння (5.79) отримаємо остаточне рівняння динаміки ланки

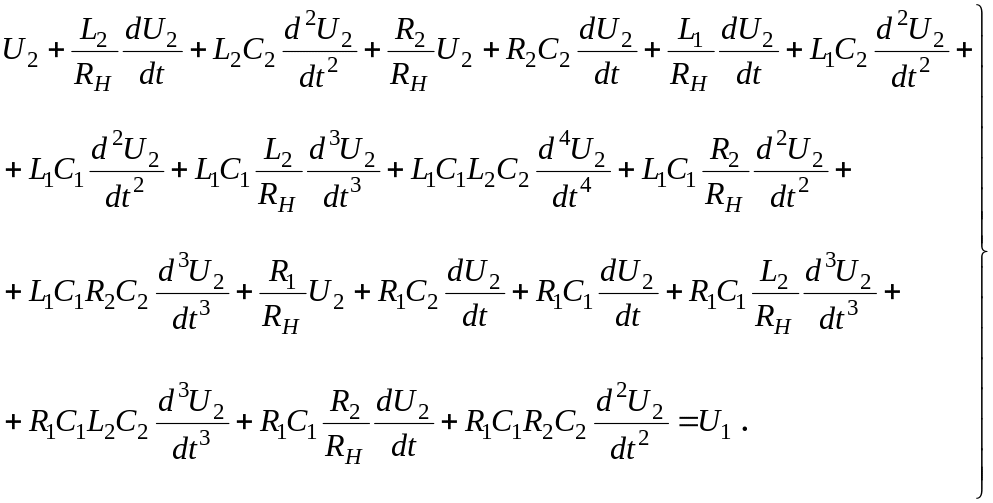(5.81)

Згрупувавши подібні члени рівняння (5.81) запишемо у вигляді

(5.82)

де

Так як рівняння (5.82) є лінійним його можна записати в абсолютних приростах

(5.83)

Введемо позначення відносних приростів , і підста­вимо їх в рівняння (5.83)

(5.84)

де .

Визначимо передатну функцію ланки. Зображення за Лапласом рівняння (5.84) має вигляд

, (5.85)

Передатна функція згідно (5.85) буде

. (5.86)

Підставивши отримаємо вираз для АФХ об’єкту

. (5.87)

Цей запис є тотожним виразу (2.71), де

(5.88)

Тоді частотні характеристики об’єкту за вхідною дією будуть визначатися виразами (2.74) – (2.77) з урахуванням позначень (5.88).