1. Angles in Space

a. Angle Between Two Lines

We know that, in space, lines can be coincident, parallel, intersecting or skew. We know finding the angle between two intersecting lines from the plane geometry. But how can we find the angle between the skew lines? In this case, on one of the skew lines we take a point and through this point we draw a line parallel to the other one. Then we get two intersecting lines and the angle between them will be the angle between the skew lines.

Note 1: If two lines are parallel, the angle between them is 0°. If two lines are perpendicular, the angle between them is 90°.

N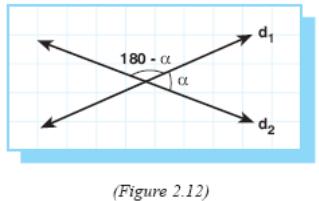 ote 2: Two lines form two different angles. By the angle between two lines, we mean the smaller one.

In Figure 2.12, we take α or 180 – α as the angle between d₁and d₂ by finding the smaller one.

b . Angle Between a Line and a Plane

Angle between a line and a plane is the angle between the line itself and its projection on that plane.

In Figure 2.13, Proj_α d = d' and ∠AOA' is the angle between d and α.

Note: If a line is perpendicular to a plane, the angle between them is 90°. If the line is parallel to that plane, the angle between them is 0°.

Theorem: Between all angles formed by a line and all of the lines in a plane, the angle with the projection of the given line is the smallest one.

P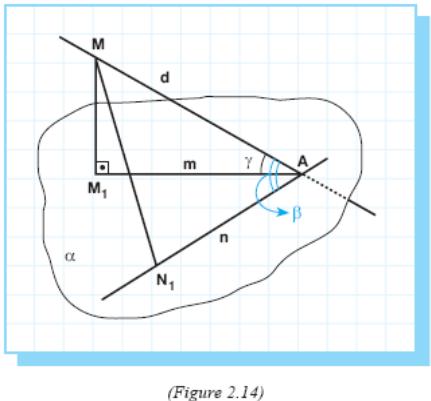 roof: Let d be a given line, m its projection on plane α and n another line in α.

On line n, take line segment AN₁ = AM₁ i.e. equal to the projection of inclined line segment MA, where M₁ is the projection of point M on d.

Then two sides of triangles AM₁M and AN₁M are equal: side AM is common to both, and AM₁ and AN₁ are equal by construction.

But the third side MN₁ in triangle AN₁M is longer than the third side MM₁ in the triangle AM₁M (an inclined line is greater than a perpendicular).

Hence the opposite angle β in ΔAN₁M is greater than angle γ in ΔAM₁M .

Therefore, β > γ.

Conclusion:

The acute angle between a line lying in a plane and the projection of an inclined line on this plane is less than the angle between the line and the inclined line.

Refer to Figure 2.14. m is the projection of n on (AM₁M) and d is another line in (AM₁M). So the angle between m and n is smaller than the angle between n and d.

c. Angle Between Two Planes (Dihedral Angle)

D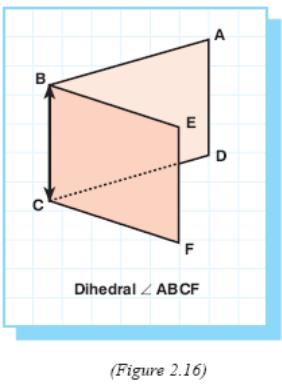 efinition: (dihedral angle, faces, edges)

A dihedral angle is a figure formed by two half planes having a common line.

The two half planes are called as the faces and their intersection line as the edge of the dihedral angle.

A dihedral angle may be read by naming a point in one

face, the edge, and a point in the other face.

Definition: (plane angle of a dihedral angle)

A plane angle of a dihedral 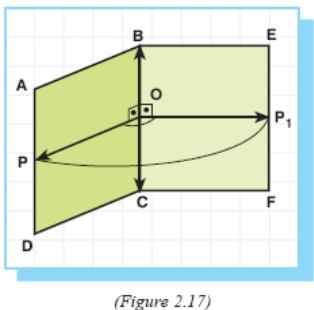angle is an angle formed by two perpendiculars drawn to the same point on the edge.

In Figure 2.17, ∠POP₁ is a plane angle of dihedral angle ABCF.

There are infinitely many plane angles of a dihedral angle.

Theorem: Plane angles of a dihedral angle are equal to each other.

P roof:

In Figure 2.18, ∠POP₁ and ∠TO₁T₁ are two plane angles of dihedral angle ABCF.

Rays OP and O₁T lie on the same face of the dihedral angle and they are perpendicular to edge BC, so they are parallel in the same direction.

Similarly rays OP₁ and O₁T₁ are also parallel in the same direction.

Therefore, ∠POP₁ = ∠TO₁T₁.

Note 1: In our book we will use dihedral angle as plane angle of dihedral angle.

Note 2: If two planes are intersecting planes, the dihedral angle between them is the smaller one. If two planes are parallel, the dihedral angle between then is 0°.

Definition: (perpendicular and oblique planes)

If the angle between two planes is 90°, planes are said to be perpendicular, otherwise they are oblique planes.

Example 52: Given an equilateral triangle ABC with one side 8 cm and point O is its centroid. Through point O, a line segment OT is drawn that is perpendicular to the plane of ΔABC. The length of OT is 4 cm. Find the angle between the planes of ΔABC and ΔABT.

S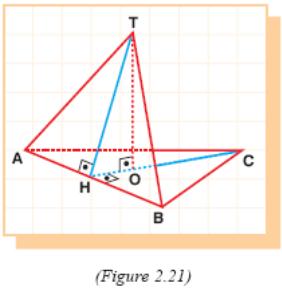 olution: Triangle ABC is equilateral so its height CH will pass through point O.

Let us draw TA and TB and join T and H (Figure 2.21).

By the three perpendiculars theorem, TH will be perpendicular to AB.

Hence, the angle between planes of ΔABC and ΔABT

will be ∠THO. Now, let us calculate this angle.

cm,

cm,

then m(THO) = 60.

Example 53: ABCD is a rhombus with ∠A = 60°. AB = 6 cm and BE ⊥ (ABC),

BE = cm. Find the angle between (AED) and (ABC).

Solution: First of all, let us draw BH ⊥ AD.

I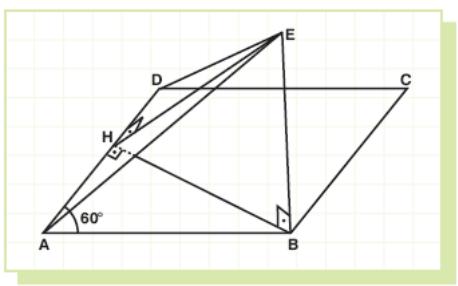 f we join E and H then EH will be perpendicular to AD by the three perpendiculars theorem.

∠EHB is the angle between planes AED and ABC. Now, let us calculate it.

In ΔAHB, BH = AB ⋅ sin60° = 6 ⋅ = cm.

In ΔEBH, BE = BH = cm.

So ΔEBH is an isosceles right triangle. Therefore, ∠EHB = 45°.

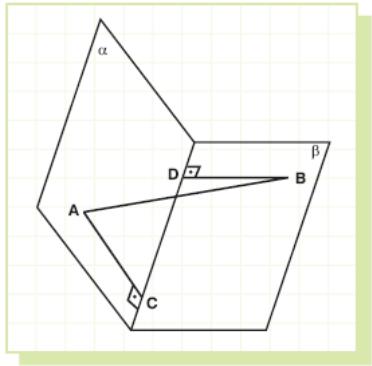
Example 54: The endpoints of line segment AB lie in the planes as in the figure. AB = 16 cm.

Two half planes make an angle of 120°.

AC and BD are perpendicular to intersection line of these two planes.

Find length of CD if AC = 7 cm and BD = 11 cm.

S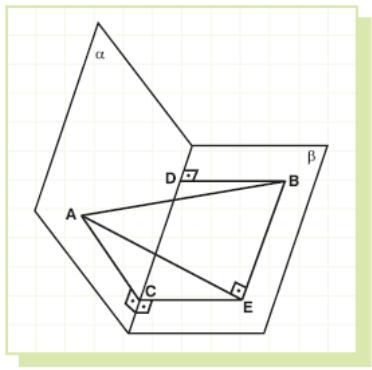 olution: In plane β, we take CE = BD that is perpendicular to intersection line of planes α and β.

So, angle ACE will be the dihedral angle between α and β, BDCE will be a rectangle.

Now, let us join A and E.

AC ⊥ CD and CE ⊥ CD, so CD ⊥ (ACE).

Since CD // BE, BE ⊥ (ACE). Thus, ∠AEB = 90°.

Now, in ΔACE by applying the cosine theorem.

AE² = AC² + CE² – 2 ⋅ AC ⋅ CE ⋅ cos (∠ACE)

AE² = 7² + 11² – 2 ⋅ 7 ⋅ 11 ⋅ cos 120°

AE² = 247.

ΔAEB is a right triangle. By the Pythagorean theorem, we have

AE² + EB² = AB² ; 247 + EB² = 16² ; EB² = 9 and EB = 3 cm.

In rectangle BDCE, EB = CD. Therefore, CD = 3 cm.

Example 55: In the adjacent figure, triangle ABC is given. Point P is not lying in the plane of ΔABC.

AB = AC = AP = 4 cm.

BC = BP = CP = 6 cm.

Calculate:

a) the angle between lines AB and CP.

b) the cosine of the angle between planes ACP and BCP.

Solution:

a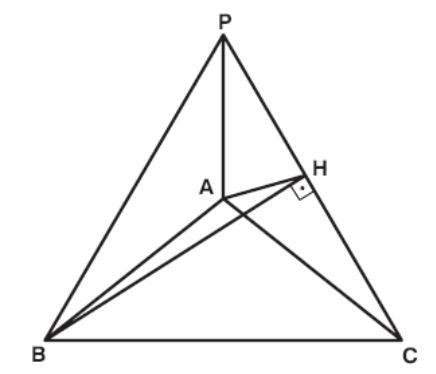 ) In ΔBPC draw height BH of side PC.

Since ΔBPC is an equilateral triangle H is the midpoint of PC.

In ΔPAC, PA = AC and H is the midpoint of

PC. So AH ⊥ PC too. Hence PC ⊥ (AHB).

Since AB is a line in (AHB), PC ⊥ AB. That means the angle between PC and AB is 90°.

b) The angle between given faces is ∠AHB, So we need to find cos ∠AHB.

cm,

cm,

AB= 4 cm.

In ΔAHB by cosine theorem:

AB² = AH² + BH² – 2 · AH · BH · cos ∠AHB,

16 = 7 + 27 – 2 · · · cos ∠AHB, then .

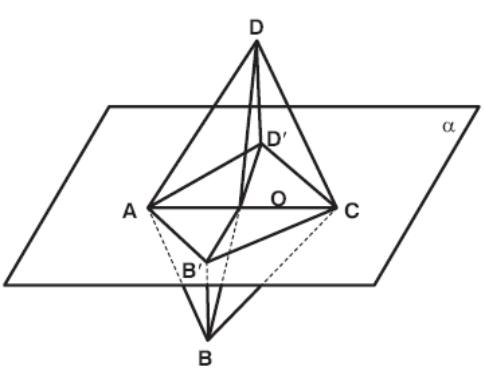
Example 56: A rhombus ABCD has AB = cm. The projection of the rhombus on a plane α which contains diagonal AC is a square AB'CD' with an area of 2 cm². Find:

a. the area of the rhombus.

b. the angle between plane ABC and plane α.

Solution:

a. Since the area of AB′CD′ is 2 cm² one side of it is cm.

DD′ ⊥ α. So DD′ ⊥ AD′.

Then cm.

Let D′B′ intersect AC at O. Then O is the midpoint of AC.

So DB intersects AC at O too, and DO = OB.

DD′ ⊥ D′O. So cm.

So DB = 4 cm.

It is obvious that AC = · = 2 cm.

Therefore the area of rhombus is

b. The intersection of (ABC) and α is AC.

DD′ ⊥ α, D′O ⊥ AC.

So by three perpendiculars theorem DO ⊥ AC.

So the angle between (ABC) and α is ∠DOD′.

Then

Check Yourself 13

1. Given an equilateral triangle ABC where G is the centroid. Point N is not in the plane of ΔABC and NG is perpendicular to the plane of ΔABC. The angle between NA and NG is 30°. If NG = cm, find side length of ΔABC.

2. Given point M and plane α such that M ∉ α. MO is perpendicular to plane α . MP and MQ are inclined to α which make 45° and 60° with plane α, respectively. Find the length of PQ in terms of MO if ∠POQ = 150°.

3. ΔABC is a right triangle with ∠C = 90° , ∠A = 30°, and AC = 3 cm. Line segment DC is perpendicular to the plane of ΔABC. If DC = cm, find the angle between (ADB) and (ABC).

4. On the faces of a dihedral angle taken 2 points which are at a distance of 6 cm and 10 cm from the edge of the dihedral angle. The distance from one of the points to the opposite face is 7,5 cm. Find the distance between the second point and its opposite face.

5. ΔABC is an equilateral triangle. Side AB makes 45° with a plane α and side AC lies in plane α. What is the tangent of the angle between planes (ABC) and α ?

6. In the adjacent figure, an equilateral triangle ABC is given. Point P is not lying in the plane of ΔABC and

PA = PB = PC = AB.

Find the cosine of the dihedral angle formed by any two faces.

Answers

1. 2. 3. 60° 4. cm 5. 6.

d. Polyhedral Angles

If you try to make a model of a three dimensional figure whose faces are all equilateral triangles except one which is a regular hexagon, you will probably find that it is impossible to build such a model. In your model the sides of the triangles should fit to form edges of three dimensional figure, but they will not, since there seems to be something wrong with the angles.

Hence, we need to investigate the properties of the angles at a vertex of three dimensional figures.

Definition: (polyhedral angle)

A figure formed by three or more planes that meet in a point and are so situated that they may be intersected by another plane to form a polygon is called a polyhedral angle.

I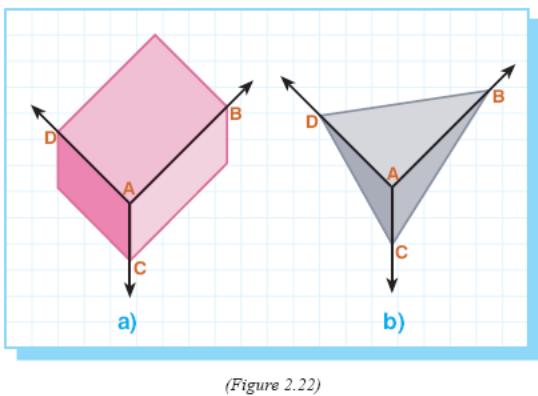 n Figure 2.22, the angles at vertex A of the three dimensional figure are ∠DAB, ∠DAC and ∠CAB. The union

of these angles and their interiors

form a polyhedral angle.

The portions of the planes which form the polyhedral angle are called its faces.

The common point of meeting of the planes is called the vertex of the polyhedral angle.

The dihedral angles formed by the faces are called the dihedral angles of the polyhedral angle.

The edges of the dihedral angles are the edges of the polyhedral angle.

A face angle of the polyhedral angle is formed by the edges of any face.

A polyhedral angle may be read by naming the vertex or by naming the vertex and a point on each edge. Thus, the polyhedral angle in Figure 2.23 may be read as “polyhedral angle P” or “polyhedral angle P-ABCDE”.

In the same figure, the surfaces containing P, A, B or P, B, C are some of the faces of the polyhedral angle.

A polyhedral angle may have many face angles. The least it may have is three. The polyhedral angle having three faces is called a trihedral angle.

Polyhedral angles of four, five, six or eight faces are called respectively tetrahedral, pentahedral, hexahedral, octahedral angles.

A polyhedral angle is convex if the section formed by a plane intersecting all the faces is a convex polygon.

Polyhedral angle V in Figure 2.24 (a) is not convex, since polygon ABCDEF in plane m is not convex. On the other hand, polyhedral angle W in part (b) is convex, since the section in plane n is a convex polygon KLMNP.

Two polyhedral angles are congruent if the face angles and dihedral angles of one are equal, each to each, to the face angles and dihedral angles of the other, and arranged in the same order.

Two polyhedral angles are symmetric, if the face angles and dihedral angles of one are equal, each to each, to the face angles and dihedral angles of the other, but arranged in opposite order.

Congruent polyhedral angles can be made to coincide, but symmetric polyhedral angles cannot. In Figure 2.25, polyhedral angles V – ABC and V – A'B'C' are symmetric and they can not be made to coincide.

We will now investigate the properties of the face angles of a convex polyhedral angle.

Theorems: 1. The sum of the measures of any two face angles of a trihedral angle is greater than the measure of the third face angle.

2. The sum of the measures of the face angles of a convex polyhedral angle is less than 360°.

3. In any trihedral angle;

a. each dihedral angle is less than 180°.

b. the sum of the dihedral angles is less than 540°.

c. the sum of the dihedral angles is greater than 180°.

4. Two trihedral angles are either congruent or symmetric if the three face angles of the one are equal respectively to the three face angles of the other.

P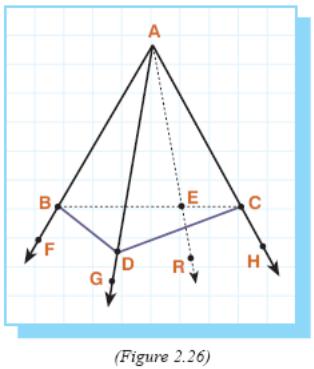 roofs:

1. Referring to Figure 2.26, polyhedral angle A – FGH is a trihedral angle whose largest face angle is angle FAH.

Let us draw ray AR in plane FAH so that ∠FAG = ∠FAR.

Choose any points B and C on rays AF and AH, respectively.

Let ray AR intersect BC at a point E.

Then select D on ray AG so that AD = AE.

Then ΔBAD ≅ ΔBAE by S.A.S. and so BD = BE .

Now, in BDC, BD + DC > BC and BC = BE + EC ⇒ DC > EC. (BD = BE)

And in ACD and ACE, AC = AC , AD = AE and DC > EC, so ∠DAC > ∠EAC.

Hence, ∠DAC + ∠BAD > ∠EAC + ∠BAE ( ∠BAD = ∠BAE )

∠DAC + ∠BAD > ∠BAC .

Since angle BAC is the largest of the three face angles, the two following inequalities can be written,

∠BAC + ∠BAD > ∠DAC and ∠BAC + ∠DAC > ∠BAD.

The proof for the case where there is no largest face angle is similar.

2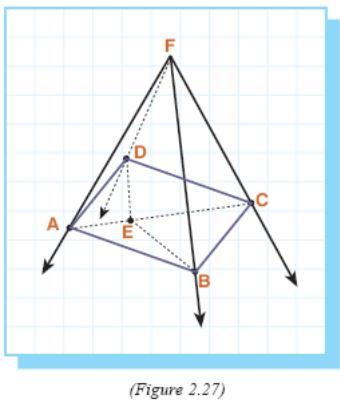 . Consider a convex polyhedral angle formed by point F and convex polygon ABCD, as illustrated in Figure 2.27.

Suppose E is any point in the interior of ABCD.

In the drawing, there are as many triangles having E as a vertex as there are triangles having F as a

vertex. (why?)

The sum of the measures of all the angles in the triangles having E as a vertex is the same as the sum of the measures of all the angles in the triangles having F as a vertex. (why?)

Hence, we may generalize the proof to all convex polyhedral angles. Namely, the number of faces of polyhedral angle F is not important and if we can prove that the sum of the measures of the face angles of polyhedral angle F is smaller than 360° then we may accept that it holds for all convex polyhedral angles.

Thus, it is enough to prove 360°>∠AFD+∠AFB+∠BFC+∠CFD.

By Theorem 2.7, for the trihedral angles at A, B, C and D, we can write

If we add both sides of the inequalities side by side, we get:

∠ADE + ∠EAD + ∠EBA + ∠BAE + ∠ECB + ∠CBE + ∠EDC + ∠DCE is smaller than ∠FAD + ∠FDA + ∠FAB + ∠FBA + ∠FCB + ∠FBC + ∠FCD + ∠FDC .

In FAD, FAB, FDC and FCB, we can write

∠FAD + ∠FDA = 180° – ∠AFD

∠FAB + ∠FBA = 180° – ∠AFB

∠FCB + ∠FBC = 180° – ∠BFC

∠FCD + ∠FDC = 180° – ∠CFD.

Similarly, in EAD, EDC, ECB and EBA, we get

∠ADE + ∠EAD = 180° – ∠AED

∠EBA + ∠BAE = 180° – ∠AEB

∠ECB + ∠CBE = 180° – ∠BEC

∠EDC + ∠DCE = 180° – ∠CED.

If we substitute these values into the above inequality, we obtain

∠AED+∠AEB+∠BEC+∠CED > ∠AFD+∠AFB+∠BFC+∠CFD.

In quadrilateral ABCD, the sum of the angles around point E is 360°.

Thus, we conclude that 360° > ∠AFD + ∠AFB + ∠BFC + ∠CFD.

3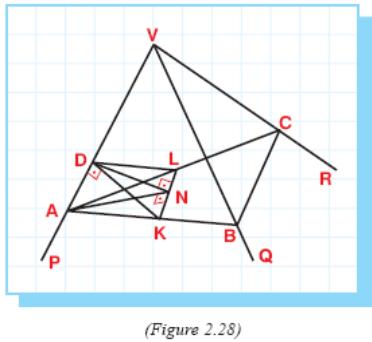 . a. In trihedral angle V-PQR, let the measures of dihedral angles VP, VQ and VR be respectively

x, y and z.

On the edges of the trihedral angle, let us choose A, B, C so that VA = VB = VC and draw AB, BC

and AC as in Figure 2.28.

Through any point D on VA, if we draw a plane perpendicular to VA, cutting face VAB along DK, face VAC a long DL and the plane of ABC along KL, then ∠KDA = ∠LDA = 90°.

Therefore, ∠KDL is the plane angle of dihedral angle VP. In other words, ∠KDL = x.

On the other hand, D-AKL is a trihedral angle.

By Theorem 2, ∠KDA + ∠LDA + ∠KDL < 360°, 90° + 90° + x < 360°.

So x < 180°.

Similarly, we can obtain y < 180° and z < 180° .

b.

So x + y + z < 540° .

c. In KDL, if we draw DN and AN so that DN ⊥ KL then by the three perpendiculars theorem, AN ⊥ KL.

Therefore, in right triangles ANK and DNK, each of angles NDK and NAK is acute.

.

Since AK is the hypotenuse of right triangle ADK, DK < AK and therefore,

sin (∠NAK) < sin (∠NDK).

In other words, m(∠NAK) < m(∠NDK) because they are both acute angles.

Similarly, we can obtain m(∠NDL) > m(∠NAL).

So, we can write, m(∠KDL) > m(∠KAL).

Since x = m(∠KDL) and m(∠BAC) = m(∠KAL), x > m(∠BAC).

In the same manner, we can prove that, y > m(∠ABC) and z > m(∠BCA).

On the other hand, in ABC, m(∠BAC) + m(∠ABC) + m(∠BCA) = 180°.

Therefore, x + y + z > m(∠BAC) + m(∠ABC) + m(∠BCA),

x + y + z > 180°.

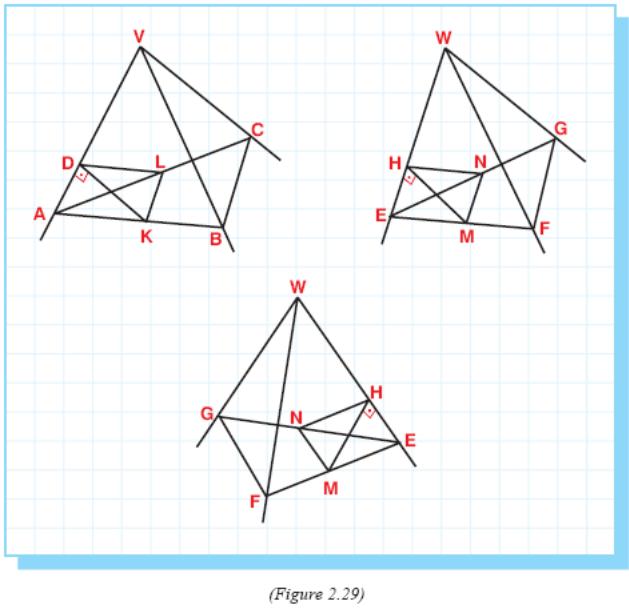
4. Let us choose points A, B, C, E, F and G on the edges of the trihedral angles so that

VA = VB = VC = WE = WF = WG and draw AB, BC, AC, EF, FG and EG as in Figure 2.29.

Given that angles AVB, BVC, CVA are equal respectively to angles EWF, FWG, GWE.

Therefore, by S.A.S., we can write

ΔAVB ≅ ΔEWF , ΔBVC ≅ ΔFWG and ΔCVA ≅ ΔGWE .

Hence, AB = EF, BC = FG and CA = GE .

By S.S.S., ΔABC ≅ ΔEFG .

So, ∠BAC = ∠FEG .

Through any point D on VA, let us draw DK in face AVB and DL in face AVC so that DK ⊥ VA and DL ⊥ VA and draw KL.

Then let us take point H on WE so that AD = EH and draw HM, HN and MN in the same manner.

Therefore HM ⊥ WE and HN ⊥ WE.

Since, ∠BAV = ∠FEW, AD = EH and ∠ADK = ∠EHM = 90°, ΔADK ≅ ΔEHM.

Therefore, AK = EM and DK = HM.

Similarly, we can get AL = EN and DL = HN.

So, by S.A.S., ΔKAL ≅ ΔMEN ( ∠BAC = ∠FEG )

Then, KL = MN and therefore, by S.S.S., ΔKDL ≅ ΔMHN.

Hence, we can conclude that ∠KDL = ∠MHN.

Namely, dihedral angles VA and WE are equal.

In the same manner, we can prove that dihedral angles VB and VC are equal to dihedral angles WF and WG respectively.

So, the corresponding parts (face angles and dihedral angles) of trihedral angles V-ABC and W-EFG are equal to each other, respectively.

By the definition, if their corresponding parts are arranged in the same order then trihedral angles V-ABC and W-EFG are congruent.

Otherwise, they will be symmetric.

Example 57: Decide whether a trihedral angle can be constructed in which the face angles are respectively

a) 60°, 40°, and 110° b) 65°, 150°, and 155°

c) 60°, 80°, and 100° d) 120°, 120°, and 120°

Solution:

a) Since the sum of the measures of any two face angles must be greater than the measure of the third face angle, the trihedral angle can not be constructed (60°+40° is not greater than 110°).

b) The sum of the measures of the face angles is greater than 360°. But by Theorem 2, it can not be. So, the trihedral angle can not be constructed with the given face angles.

c) Sum of any two face angles is always greater than the third one and sum of all face angles is smaller than 360° so it is possible to construct a trihedral angle.

d) Sum of the face angles must be smaller than 360° but 120° + 120° + 120° = 360°. So it is not possible to construct. When we add them we will get a plane.

Example 58: Can a trihedral angle be constructed with the following dihedral

angles?

a) 70°, 45°, 45° b) 60°, 185°, 35°

c) 90°, 90°, 90° d) 20°, 30°, 120°

Solution: a) Since the sum of the dihedral angles is less than 180°, the trihedral angle cannot be constructed.

b) The trihedral angle cannot be constructed because one of the dihedral angles is greater than 180°.

c) Each dihedral angle is smaller than 180°, sum of the angles is between 180° and 540° so it is possible to construct a trihedral angle.

d) Since the sum of the dihedral angles is 20° + 30° + 120° = 170 < 180°, the trihedral angle cannot be constructed.

Check Yourself 14

1. Decide whether a trihedral angle can be constructed in which the face angles are respectively

a) 80°, 80°, and 150° b) 65°, 50°, and 135°

c) 70°, 80°, and 90° d) 100°, 120°, and 140°

2. Can a trihedral angle be constructed with the following dihedral angles?

a) 170°, 45°, 65° b) 60°, 105°, 45°

c) 70°, 80°, 25° d) 120°, 230°, 140°

Answers

1. a. Yes b. No c. Yes d. No

2. a. Yes b. Yes c. No d. No

e. Length of Projection of a Line Segment

Theorem: The length of the projection of a line segment on a plane is equal to the product of the length of the line segment by the cosine of the angle between the line segment and the plane.

length_projection = length_figure . cos 

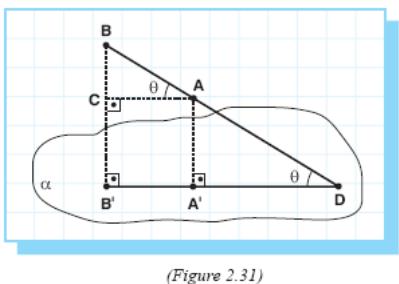
Proof: Given line segment AB and plane α.

A'B' = Proj_α AB , θ is the angle between AB

and α (Figure 2.31).

Draw AC ⊥ BB' where C ∈ BB'.

Quadrilateral ACB'A' is a rectangle. So, AC = A'B'.

ΔACB is a right triangle, .

Therefore, .

f. Area of Projection of a Figure

Theorem: The area of the projection of a polygon on a plane is equal to the product of the area of the polygon and the cosine of the angle between the planes of polygon and its projection.

Area_projection = Area_figure . cos 

Proof:

We will prove this theorem for a triangle first and then generalize for all polygons.

Let us take a triangle ABC and a plane α. There are 3 possible cases:

1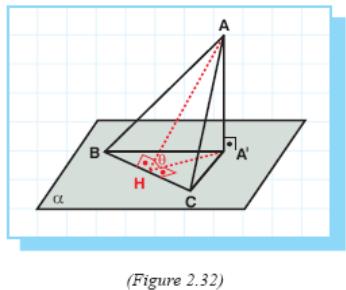 st case: If one side of ΔABC lies on plane α.

(Say side BC)(Figure 2.32).

Draw AA' ⊥ α where A' ∈ α.

We have ΔA'BC = Proj_α ΔABC.

Draw AH ⊥ BC.

By the three perpendiculars theorem, A'H ⊥ BC and therefore ∠AHA' = θ is the angle between planes of ΔABC and α.

In ΔA'BC,

In ΔAA'H,

.

2 nd case: If one side of ΔABC (Say BC) is parallel to plane α then we take another plane β such that BC ∈ β and α // β (Figure 2.33).

ΔA'B'C' = Proj_α ΔABC

ΔNBC = Proj_β ΔABC.

We know that ΔNBC ≅ ΔA'B'C'.

So A(ΔNBC) = A(ΔA'B'C') which means that A(ΔA'B'C') = A(ΔABC) ⋅ cos θ where θ is the angle

between planes of ΔABC and α.

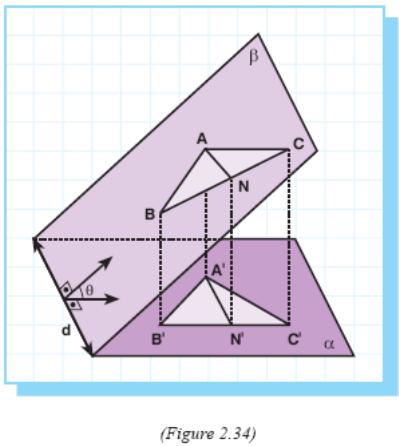
3rd case: If ΔABC is not on plane α with no side parallel to plane α (Figure 2.34).

Let β be the plane of ΔABC.

Let α ∩ β = d.

Draw AN // d where N ∈ BC and A'N' = Proj_α AN.

Then A'N' // d.

So, for ΔABN and ΔANC, we can apply 2nd case.

Let θ be the angle between planes α and β.

A(ΔA'B'N') = A(ΔABN) ⋅ cos θ

A(ΔA'N'C') = A(ΔANC) ⋅ cos θ

+ .

A(ΔA'B'C') = A(ΔABC) ⋅ cos θ

4 th case: If we have a polygon, the area of its projection on a plane can be calculated easily by dividing this polygon into triangles and finding the sum of areas of projections of each triangle on the given plane.

Let A₁B₁C₁D₁E₁ be the projection of polygon ABCDE on plane α (Figure 2.35).

Divide ABCDE into triangles ABC, ACD and ADE.

Let θ be the angle between plane of ABCDE and plane α.

Now, A(A₁B₁C₁D₁E₁) = A(ΔA₁B₁C₁) + A(ΔA₁C₁D₁) + A(ΔA₁D₁E₁)

= A(ΔABC) ⋅ cosθ + A(ΔACD) ⋅ cosθ + A(ΔADE) ⋅ cosθ

= (A(ΔABC) + A(ΔACD) + A(ΔADE)) ⋅ cosθ

= A(ABCDE) ⋅ cosθ

Example 59: Given two planes α and β. Equilateral triangle ABC whose one side length is a units lies in plane α. The angle between planes α and β is 60°. Find the area of projection of ΔABC on plane β.

S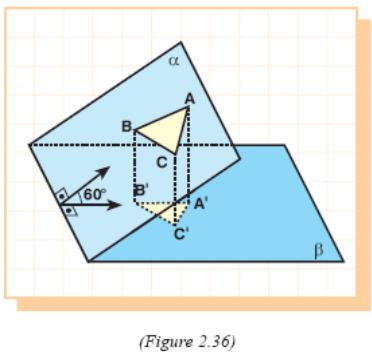 olution:

ΔABC is equilateral, so A(ΔABC) = .

Let ΔA'B'C' = Proj_β ΔABC.

A(ΔA'B'C') = A(ΔABC) ⋅ cos 60°.

.

Example 60: Area of ΔABC is 30 cm². The projection of ΔABC on a plane is ΔA'B'C' with side lengths 6 cm, 10 cm and 14 cm. Find the angle between the planes of these triangles.

Solution: Let θ be the angle between planes of ΔABC and ΔA'B'C'.

We know that A(ΔA'B'C') = A(ΔABC) . cos α.

So, we just need to find A(ΔA'B'C').

We know all side lengths of ΔA'B'C' so by using the Heron’s Formula:

.

then α = 30.

Example 61: What is the measure of the angle between the planes of a triangle and its projection if the area of its projection is half of the area of the triangle itself?

Solution: Let S be area of the triangle and S₁ be area of its projection.

Let α be the angle between their planes.

Now, it is given that S = 2S₁.

From the formula, S₁ = S ⋅ cos α, S₁ = 2S₁ ⋅ cos α.

So cos α = and α = 60° .

Example 62: Given a regular hexagon with one side a = 8 cm. The angle between the plane of the hexagon and its projection plane is 30°. Find the area of the projection of this hexagon.

Solution: We know that the area of a regular hexagon with one side a is equal to .

So,

Here, the angle between two planes is 30°.

Therefore,

Example 63: If two lines intersect at an angle of 60° and each makes an angle of 45° with a plane, show that the projections of these lines on the plane are perpendicular to each other.

S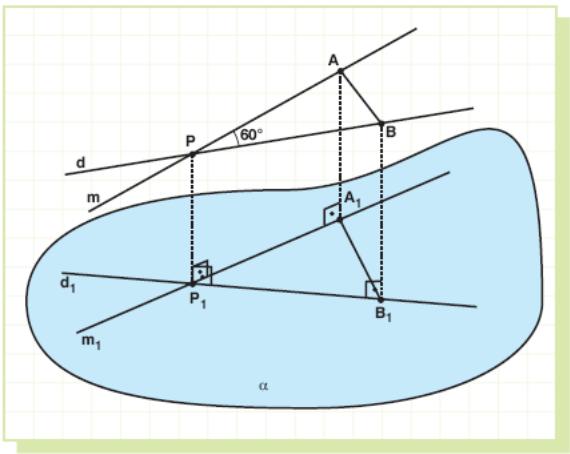 olution: We are given two lines d and m, and projection plane α.

Let us take d ∩ m = P, Proj_α d = d₁,

Proj_α m = m₁, and Proj_α P = P₁.

Now we take two points A and B on m and d, respectively such that PA = PB = k units.

Let Proj_α A = A₁ and Proj_α B = B₁.

ΔPAB will be equilateral because ∠APB = 60° and PA = PB. Therefore, PA = PB = AB = k units.

It is given that lines make 45° with plane α.

Now, P₁A₁ = PA ⋅ cos45° = k ⋅ and P₁B₁ = PB ⋅ cos45° = k ⋅ .

P₁B₁PB and P₁A₁AP are congruent trapezoids, so A₁A = B₁B and A₁ABB₁ is a rectangle.

It is obvious that AB = A₁B₁ = k.

So, in ΔP1A1B1 if we apply the Pythagorean theorem we will have,

P₁A₁² + P₁B₁²= .

That means ∠A₁P₁B₁ = 90°.

Therefore, projection lines are perpendicular.

Example 64: ABCD is a rectangle. Through vertex A, line AM is inclined to the

plane of rectangle ABCD. AM makes 60° with sides AD and AB.

Find the angle between AM and plane of rectangle.

S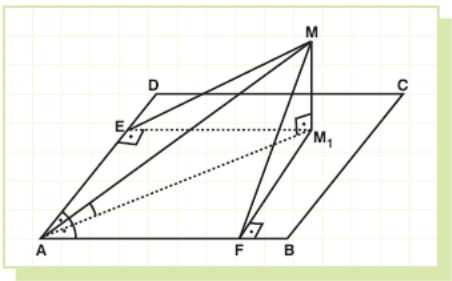 olution: Let us draw MM₁ ⊥ (ABCD).

Point M₁ will be on the bisector of ∠BAD.

Let us explain why.

Draw M₁E ⊥ AD and M₁F ⊥ AB, then

∠AEM = 90° and ∠AFM = 90°. (three perpendiculars theorem)

So, ΔAEM ≅ ΔAFM (A.A.A.).

Therefore, EM = FM which means their projections EM₁ and FM₁ are equal.

From here we can conclude that AFM₁E is a square and AM₁ is the angle bisector.

Now, let AM = a.

In ΔAME, we get AE = AM ⋅ cos60° = .

.

Finally, the angle between AM and plane of the rectangle, which is ∠MAM₁, can be found as,

So MAM₁ = 45.

Check Yourself 15

1. Given a rhombus with diagonals 10 cm and 4 cm. The angle between the plane of rhombus and the projection plane is 60°. Find the area of the projection of the rhombus.

2. What is the measure of the angle between the planes of a triangle and its projection if the area of its projection is equal to the area of the triangle itself?

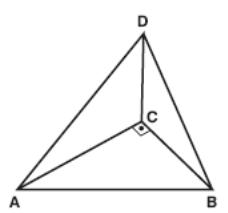
3. Given a right triangle ABC where the lengths of legs are 6 cm and 7 cm, ∠ACB = 90°. Line segment CD is perpendicular to the plane of ΔABC.

Find the area of ΔABD if its height DM makes 45° with the

plane of ΔABC.

4. Given a triangle with an area of 90 cm². Its orthogonal projection on a plane is also a triangle with side lengths 6,5 cm, 15 cm and 18,5 cm. Find the angle between the planes of these triangles.

5. In the figure d₁//Q. Angle between d₂ and Q is 30.

Given that AC = 8 cm, BD = 12 cm and d₁ is perpendicular to d₂.

Find the area of the quadrilateral that we get by connecting the projections of A, B, C and D.

Answers

1. 10 cm² 2. 0° 3. cm² 4. 60° 5. cm²