I. Projection of a Point on a Plane

The projection of a point on a plane is the foot of the perpendicular drawn from the point to the plane.

If the point is on the plane then its projection on this plane will be itself.

In Figure 2.5,

Proj_α A = A' and Proj_αB = B

II. Projection of a Line on a Plane

The projection of a line on a plane is the set of all points which are the projections of each point of the line on the plane.

If the line is perpendicular to the plane its projection will be a point.

Otherwise, its projection will be a line.

In Figure 2.6, Proj_α l = l '

III. Projection of a Figure on a Plane

P rojection of a figure on a plane is the set of all points which are the projections of all points of the figure on the plane.

Some figures may have projections different from themselves. For example, projection of a circle may be an ellipse, also it may be a line segment.

Theorems:

1. The projection of a line, not perpendicular to a plane, is also a line.

2. The projections of parallel lines not perpendicular to a plane are also parallel.

3. The projections of parallel and equal line segments on a plane are also parallel and equal.

4. The projection of a right angle on a plane, whose one arm is parallel and the other arm is not perpendicular to that plane, is also a right angle.

Proofs:

1 . Given a line l and a plane α such that l ⊥ α (Figure 2.7).

All perpendiculars drawn from line l to plane α are parallel to each other.

Let β be the plane determined by l and one of these perpendiculars.

Then all perpendiculars drawn from l to α will be in β, so the feet of all these perpendiculars will lie on the intersection line of planes α and β which is l' .

Therefore, Proj_α l = l'.

2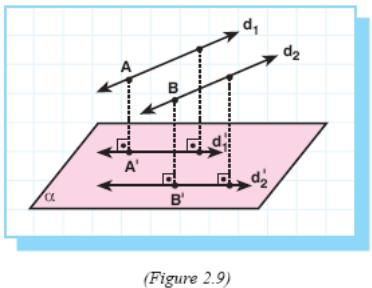 . Given lines d₁, d₂ and plane α such that d₁ // d₂,

d₁ ⊥ α and d₂ ⊥ α (Figure 2.9).

Let d₁' = Proj_α d₁ and d₂' = Proj_α d₂ .

Take A ∈ d₁ and B ∈ d₂ .

If A' = Proj_α A and B' = Proj_α B then AA' ⊥ α and BB' ⊥ α .

AA' // BB' because, two lines perpendicular to the same plane are parallel.

Since AA' // BB' and d₁ // d₂ then plane formed by AA' and d₁ is parallel to the plane formed by BB' and d₂.

Hence their intersection lines d₁' and d₂' with plane α are also parallel to each other.

3 . We proved that the projections of two parallel lines on a given plane are parallel.

So if two line segments are parallel, their projections on a given plane are parallel.

Now we will prove that the length of projections are equal.

Take two line segments AB and CD such that

AB // CD and AB = CD.

Let A'B' = Proj_α AB and C'D' = Proj_α CD.

The quadrilateral ABCD is a parallelogram because AB // CD and AB = CD.

In a parallelogram opposite sides are parallel and equal. Therefore AD // BC and AD = BC. (I)

AA' and BB', are perpendicular to α. So AA' // BB' (II).

From (I) and (II), (AA'D'D) // (BB'C'C). So A'D' // B'C'.

We know that A'B' // D'C'. Therefore quadrilateral A'B'C'D' will be a parallelogram.

Finally, we get A'B' = C'D'.

4. Given an angle BAC where ∠BAC = 90° and AB // α.

Let ∠B'A'C' = Proj_α ∠BAC (Figure 2.11).

We need to prove that ∠B'A'C' = 90°.

Since AB // α , AB // A'B'.

Since AB // A'B' and AB ⊥ AC , AC ⊥ A'B'.

So, A'B' is perpendicular to the plane formed by AA' and AC.

Therefore, A'B' ⊥ A'C' which means ∠B'A'C' = 90°.

Example 48: Given a triangle ABC and its orthogonal projection A₁B₁C₁. The distances between corresponding vertices of these triangles are a, b and c. Show that the distance between their centroids is .

S olution:

Let AM and A₁M₁ be the medians to CB and C₁B₁ in ΔABC and ΔA₁B₁C₁ respectively.

Let O and O₁ be centroids of ΔABC and ΔA₁B₁C₁, respectively.

CC₁ // BB₁ (we are taking projections so they are

perpendicular to projection plane which means they are parallel to each other).

So CBB₁C₁ will be a trapezoid and MM1 is its middle base.

and MM₁ // CC₁. So M₁M₁ // A₁A which means that AA₁M₁M is a trapezoid.

Draw AK ⊥ MM₁.

Let OO₁ ∩ AK = T.

ΔAMK ∼ ΔAOT so . (O is centroid)

M₁K = O₁T = AA₁ = a.

MK = MM₁ – M₁K = .

.

.

Example 49: Given two intersecting planes α and β where l is their intersection

line. Line b is perpendicular to plane β. Show that projection of line b on plane α is perpendicular to line l.

Solution:

If b // α then the projection of b on α will be parallel to b.

Then projection will be perpendicular to β too.

S ince l is a line in β the projection will be perpendicular to l.

If b // α then b intersects α at a point B.

Let A be the intersection of b and β.

Let A₁ be the projection of A on α. Then BA₁ will be the projection of b on α.

Let C be the intersection of BA₁ and l.

Since b ⊥ β, b ⊥ l and since AA1 ⊥ α, AA₁ ⊥ l.

So l ⊥ AA₁, l ⊥ b, that means l ⊥ (BCA).

Therefore, l ⊥ BC.

Example 50: Given an isosceles ΔABC (AB = AC). Through BC passes a plane α. Show that projection of ΔABC on plane α is also an isosceles triangle.

S olution: Let A₁ be the projection of A on α.

AB = AC is given.

We need to prove that A₁B = A₁C. Because the projection of ΔABC on α is ΔA₁BC.

Since AA₁ ⊥ α, AA₁ ⊥ BA₁ and AA₁ ⊥ CA₁.

Then and .

Since AB = AC, A₁B = A₁C.

E xample 51:

Side AD of parallelogram ABCD lies in plane α.

AB = 15 cm, BC = 19 cm. The lengths of projections of diagonals of the parallelogram on plane α are 20 cm and 22 cm. Find the distance from side BC to plane α .

(Hint: In a parallelogram e² + f² = 2 (a² + b²) where a, and b are the sides of parallelogram and e, f are the diagonals of it.)

Solution:

S ince CC₁ ⊥ α then CC₁ ⊥ AC₁, and since BB₁ ⊥ α,

BB₁ ⊥ B₁D.

Since BC // AD, BC // α and CC₁ = BB₁.

So BD² = DB₁² + BB₁² = DB₁² + CC₁²

AC² = AC₁² + CC₁²

Add both sides of these equations:

BD² + AC² = DB₁² + AC₁² + 2CC₁²

One of DB₁ and AC₁ is 20 cm and the other is 22 cm. So

BD² + AC² = 20² + 22² + 2CC₁²

We know that BD² + AC² = 2(AB² + BC²) = 2 · (15² + 19²).

So 20² + 22² + 2CC₁² = 2 · (15² + 19²).

Then 2CC₁² = 288, CC₁² =144 and CC₁ = 12 cm.

Check Yourself 12

1. Prove that projection of the midpoint of a line segment on a plane is the midpoint of the projection of that line segment on the given plane.

2. Prove that the projections of parallel and equal line segments on a line are equal.

3. The area of a square is 64 cm². One of the diagonals of this square is parallel to a line d. Find the length of the projection of this square on the line d.

4. What can we say about the projection of a right angle in a plane if one arm of the right angle is parallel to that plane and other arm is perpendicular to that plane?

5 . In the figure d₁ and d₂ are skew lines and both of them are parallel to the plane P.

State the following as true or false.

a. Projections of d₁ and d₂ in plane P are line segments.

b. Projections of d₁ and d₂ in plane P are always perpendicular to each other.

c. Projections of d₁ and d₂ in plane P always intersect each other.

d. d₁ and d₂ are always perpendicular to each other.

Answers

2. Hint: Use the same method in the proof of theorem 3.

3. cm. 4. The projection of the angle will be a ray (or a line segment).

5. a. False b. False c. True d. False

B. USING PROJECTION IN CALCULATIONS