3. Projection geometry
A. TYPES OF PROJECTION
In plane geometry we know how to find the angle between two points, a point and a line, two lines. Also we learned how to find the distance between the points and lines. To find the same things in space geometry we need to use the projection. There are two types of projections; central projection and orthogonal projection.
1. Central Projection
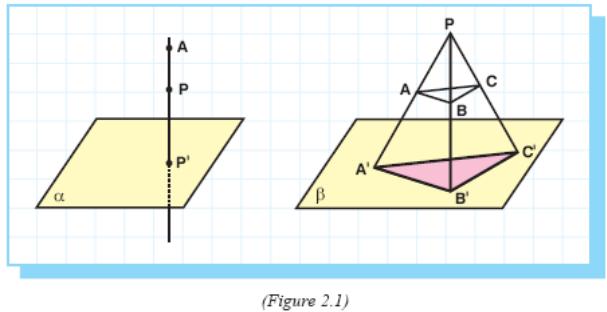
If A is a fixed point not in plane α and P is any other point, the projection of P on α is point P' where line AP intersects α.
The central projection of a geometric figure upon a plane consists of the projections of all points of the figure. For example, the central projection of ΔABC from point P upon plane β is ΔA'B'C' (Figure 2.1).
The central projection of an object may not have the same shape as the object. For example, a central projection of a circle may be an ellipse. Projective geometry is a study which deals with the properties of figures which are not changed by projection.
2. Orthogonal Projection
A figure is projected orthogonally when the projecting lines are perpendicular to the plane of the projection. Since the projecting lines are perpendicular to the plane of the projection, they are parallel to each other.
In this book, we will use only orthogonal projection. Therefore, unless otherwise stated, “projection” will mean “orthogonal projection”.
a. Projection on a Line
I. Projection of a Point on a Line
Definition: (projection)
The projection of a given point on a line is the point which is the foot of the perpendicular drawn from the point to line.
I
n
Figure 2.2, A' is the projection of A on line l
and
AA' is the distance from point A to line l.
If point A is on line l then its projection will be itself and the distance will be zero.
We can show the projection of point A on line l shortly as Proj l A .
In this case Proj l A = A'
II. Projection of a Line Segment on a Line in a Plane
Projection of a line segment on a line is the set of all points which are the projections of each point of the line segment on the line.
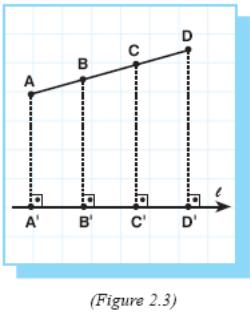
In Figure 2.3, A, B, C and D are some points on line segment AD and A', B', C' and D' are points on l such
That A', B', C' and D' are the projections of A, B, C, D on l respectively.
Then Proj l AD = A'D'.
For each part we can write the projection in a similar way, like
Proj l AB = A'B' and Proj l CD = C'D'.
By
Thales theorem we can easily get the proportion
.
Note: If the line segment is parallel to the given line then the length of its projection on that line will be equal to the length of itself. If it is perpendicular then its projection will be a point, hence the length of the projection will be zero.
III. Projection of a Figure on a Line in a Plane
P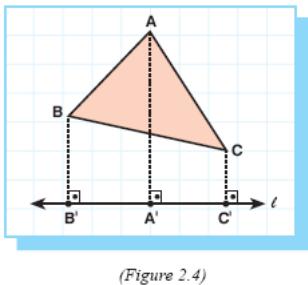
rojection
of a figure on a line is the set of all points which are the
projections of each point of the figure on the given line.
In Figure 2.4, the projection of ΔABC on line l is line
segment B'C'.
Projl ΔABC = B'C'.
Note: In order to find the projection of a figure on a line, the figure and the line must be in the same plane.
b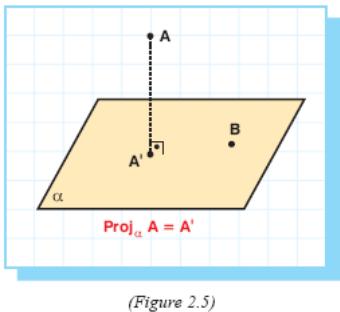
.
Projection on a Plane