МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ „ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Чисельні методи розв’язування нелінійних рівнянь методичні вказівки

до виконання лабораторної роботи № 1

з дисципліни „Чисельні методи”

для студентів спеціальності

6. 050103 „Програмна інженерія”

Затверджено на засіданні кафедри програмного забезпечення Протокол № __ від _______ р.

Львів – 2012

Чисельні методи розв’язування нелінійних рівнянь. Методичні вказівки до виконання лабораторної роботи № 1 із дисципліни „Чисельні методи” для студентів спеціальності „Програмна інженерія” / Укл.: Н. Б. Мельник, О.О. Нитребич – Львів: Видавництво Національного університету „Львівська політехніка”, 2012. – 25 с.

Укладачі Мельник Н.Б., ст.викладач кафедри ПЗ

Нитребич О.О., асистент кафедри ПЗ

Відповідальний за випуск Федасюк Д.В., д-р тех. наук, проф.

Рецензенти

Зміст

Мета роботи……………….……………………………………………………4

Теоретичні відомості…………………………………………………………..4

1. Класифікація нелінійних рівнянь…………………………………………..4

2. Методи відокремлення коренів …………………………………,,………..6

2.1. Графічний метод ……………………………………………………. 7

2.2 Аналітичний метод…………………………………………………… 8

3. Чисельні методи уточнення коренів……………………………………….10

3.1. Метод поділу відрізка навпіл…………………………………………10

3.2. Метод хорд ………………………………………………………….…12

3.3. Метод Ньютона (метод дотичних) …………………………………...15

3.4. Метод ітерацій (метод послідовних наближень) ……………………18

4. Приклади розв’язування задач …….………………………………………20

Варіанти завдань……………………………………………………………… 23

Вимоги до звіту ……………………………………………….………………23

Вимоги до програми …………………………………..………………………23

Контрольні запитання ……………………………. ………………………… 24

Список літератури……………………………………………………………..25

Мета роботи: Ознайомлення з методами відокремлення дійсних ізольованих коренів нелінійних рівнянь та ітераційними методами їх уточнення.

Теоретичні відомості

Математичними моделями багатьох об’єктів і процесів навколишнього світу є нелінійні рівняння та їх системи: алгебраїчні і трансцендентні – для сталих станів, диференціальні – для динамічних процесів. Розглянемо методи розв’язування нелінійних алгебраїчних та трансцендентних рівнянь.

На відміну від лінійних рівнянь не існує прямих методів розв’язання нелінійних рівнянь. Процедура побудови розв’язку нелінійного рівняння складається з двох етапів:

• локалізація коренів – визначення інтервалів, що містять єдиний корінь,

• уточнення коренів.

1. Класифікація нелінійних рівнянь

В обчислювальній практиці часто доводиться розв’язувати нелінійні рівняння виду:

, (1)

де деяка неперервна функція. Такі рівняння можна розділити на дві групи - алгебраїчні і трансцендентні.

Алгебраїчні рівняння містять тільки алгебраїчні функції (раціональні та ірраціональні). Рівняння, які містять інші функції (тригонометричні, показникові, логарифмічні і т.п.), є трансцендентними.

Функція називається раціональною, якщо її можна записати у вигляді многочлена

y=a₀x_n+a₁x_n-1+...+a_n, (2)

де n – степінь многочлена (ціле невід’ємне число), a₀,a₁,…,a_n – його коефіцієнти.

Функція називається ірраціональною, якщо вона є суперпозицією раціональної функції та степеневої функції із раціональними показниками.

Приклади алгебраїчних рівнянь:

1. y=0.5x⁴+x+1 – раціональне рівняння;

2. y= x² – раціональне рівняння;

3. – ірраціональне рівняння;

4. – ірраціональне рівняння.

Приклади трансцендентних рівнянь:

1. – трансцендентне рівняння з використанням логарифмічної функції;

2. – трансцендентне рівняння з використанням показникової функції;

3. – трансцендентне рівняння з використанням тригонометричної функції;

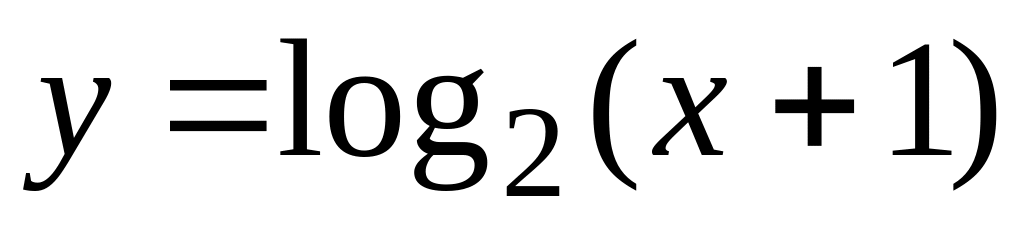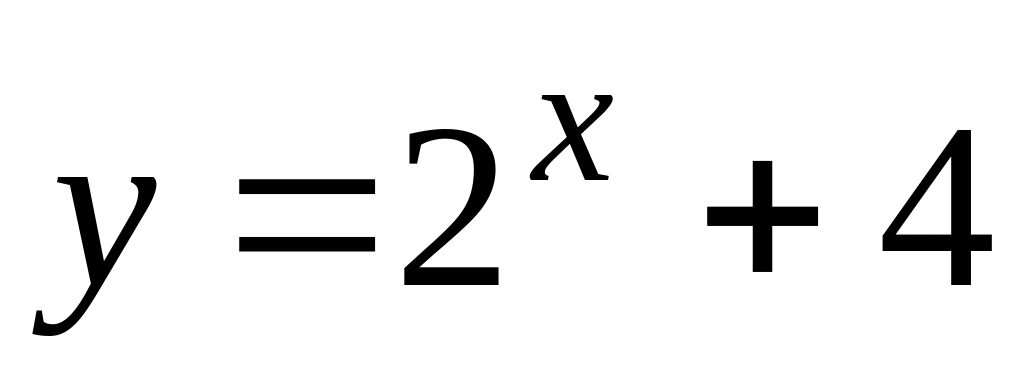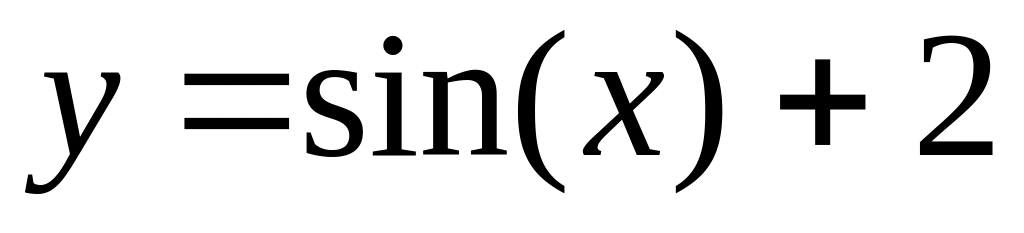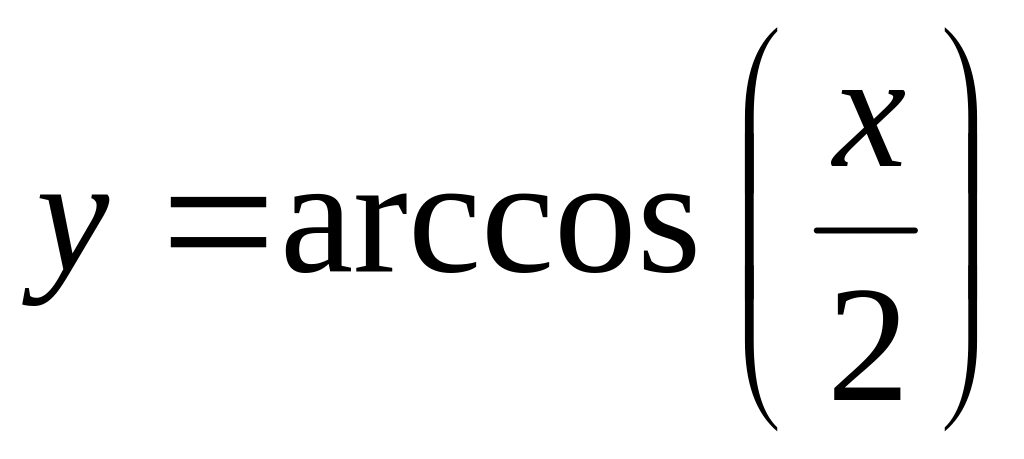4. – трансцендентне рівняння з використанням оберненої тригонометричної функції.

Розв’язком нелінійного рівняння називається вектор , координати якого при підстановці в початкове рівняння (1), перетворюють його в тотожність.

Методи розв’язування нелінійних рівнянь поділяються на точні і ітераційні. Точні методи дозволяють отримати корінь рівняння в результаті виконання скінченної кількості арифметичних операцій. Іншими словами, ці методи дозволяють записати корінь у вигляді деякого співвідношення. Однак переважно для розв’язування нелінійних рівнянь використовуються чисельні (наближені ітераційні) методи.

Реалізація чисельних методів складається з двох етапів:

1) відшукання наближеного значення кореня або відрізка, що його містить;

2) уточнення наближеного значення кореня.

Наближене значення кореня (початкове наближення) можна знайти з фізичних міркувань. Наприклад, знайти два значення : a і b, в яких функція буде приймати значення різних знаків, тобто . Тоді між a і b є принаймні одне значення х, для якого . В якості цього х наближено можна взяти, наприклад, значення .

Ітераційні методи полягають у послідовному уточненні початкового наближення . В результаті ітерацій знаходиться послідовність наближених значень кореня . Якщо при цьому із збільшенням n значення наближаються до точного розв'язку рівняння, то кажуть, що даний ітераційний процес збіжний.

Розглянемо особливості етапу відокремлення коренів.