Критичний стан. Критичні параметри. Зведене рівняння Ван дер Ваальса

На рис.5.3,а зображено сімейство ізотерм Ван дер Ваальса, отриманих вперше експериментально англійським фізиком Томасом Ендрюсом.

П

а б

Рис.5.3

ри високих температурах вигляд ізотерм співпадає із ізотермами ідеального газу. При зниженні температури на ізотермі спочатку з’явиться перегин при , а потім і ділянка сталого тиску. Точка перегину має назву критичної точки, а параметри, якими характеризується газ у цій точці,  критичними параметрами .

При при стисненні газу відбувається його перехід у рідкий стан. Відповідні фази вказані на рис.5.3,б.

Щоб знайти критичні параметри, перепишемо рівняння (5.4) у вигляді

. (5.6)

У критичній точці і . З цих умов отримаємо критичний об’єм – найбільший об’єм рідини для даного стану

, (5.7)

критичну температуру – температуру, вище якої газ не можна зрідити

, (5.8)

критичний тиск – найбільший тиск насиченої пари

. (5.9)

Увівши відносні параметри: зведений тиск , зведений об’єм , зведену температуру , отримаємо зведене рівняння Ван дер Ваальса

. (5.10)

У такому вигляді рівняння стану не містить ніяких індивідуальних параметрів речовини, отже, зведені рівняння стану однакові для всіх речовин.

Ефект Джоуля-Томсона. Коефіцієнт Джоуля-Томсона

Е

Рис.5.4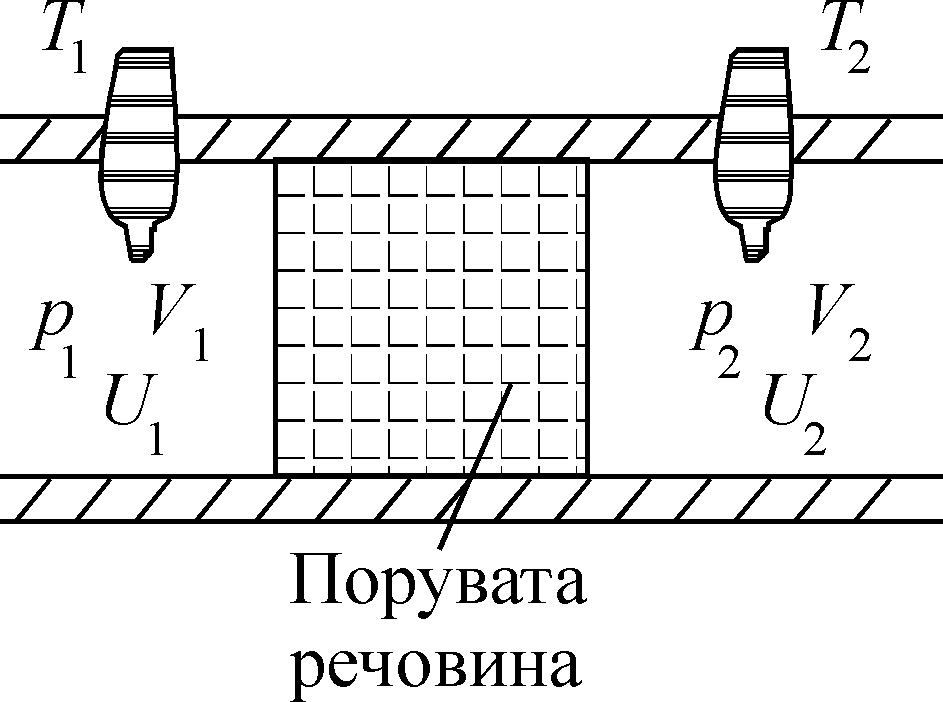

фект Джоуля-Томсона полягає у зміні температури газу при дроселюванні, тобто повільному протіканні газу під дією сталого градієнта тиску крізь місцеву перешкоду газовому потоку. Ефект був відкритий на підставі дослідів, проведених у 1852-1862 роках Джеймсом Джоулем і Вільямом Томсоном (лорд Кельвін).

Дослід Джоуля-Томсона ілюструє рис.5.4. Посеред адіабатно ізольованої труби розміщувалась перегородка з поруватої речовини (дросель). За рахунок різниці тисків по обидва боки перегородки газ продавлювався через нього. Дросель забезпечував малу швидкість газового потоку, що дозволяє не враховувати його кінетичну енергію. Тиски газів і по різні боки дроселя підтримувались сталими. Після встановлення стаціонарної течії газу через дросель по обидва боки від нього встановлювались температури і (рис.5.4). Чим ближче були властивості газу до ідеального, тим меншою була різниця температур.

Така стаціонарна течія газу через порувату речовину називається процесом Джоуля-Томсона. Хоча він відбувається за умов адіабатної ізоляції системи, цей процес відрізняється від адіабатного. Адіабатний процес є квазірівноважним, всі порції газу мають однакові температуру і тиск. Процес Джоуля-Томсона є лише стаціонарним, тиски і температури по різні боки дроселя відрізняються.

Важливою особливістю ефекту Джоуля-Томсона є те, що він йде без зміни ентальпії . Дійсно, виділена порція газу, що займала об’єм при тиску , після проходження дроселя займатиме об’єм при тиску . Оскільки теплообмін відсутній, перший закон термодинаміки (закон збереження енергії) матиме вигляд , де і – внутрішня енергія газу до і після дроселювання, – робота решти газу по стисненню виділеної порції до дроселя, – робота розширення цієї порції після нього. Оскільки величина є ентальпією, або тепловою функцією, процес Джоуля-Томсона є ізоентальпійним.

Кількісно ефект Джоуля-Томсона характеризується швидкістю зміни температури із тиском за сталої ентальпії – коефіцієнтом Джоуля-Томсона

. (5.11)

Для знаходження коефіцієнта Джоуля-Томсона у явному вигляді запишемо повний диференціал ентальпії

. (5.12)

Оскільки за означенням ентальпія , то, з іншого боку, з означення ентропії та першого закону термодинаміки , де – ентропія системи, отже

. (5.13)

З (5.13) маємо

. (5.14)

Застосовуючи метод термодинамічних потенціалів, використаємо одне з рівнянь зв’язку Максвелла

,

тоді (5.14) набуває вигляду

. (5.15)

При ізобарному процесі , отже . Підставивши (5.12) отримані вирази для частинних похідних, отримуємо

.

За сталої ентальпії , тоді коефіцієнт Джоуля-Томсона

. (5.16)

Легко переконатись, що для ідеального газу , , а . Отже, у ідеальному газі температура не змінюється із тиском, що і отримали експериментально Джоуль і Томсон.

Для знаходження величини скористаємось рівнянням Ван дер Ваальса (5.4). Розкривши дужки і продиференціювавши по температурі за сталого тиску, знайдемо

. (5.17)

Підставивши вираз для тиску (5.6) в рівняння (5.17), а отриманий результат в (5.16), після очевидних перетворень маємо вираз для коефіцієнта Джоуля-Томсона

. (5.18)

Для подальшого аналізу отриманого виразу скористаємось штучним прийомом – з рівняння Ван дер Ваальса (5.6) знайдемо похідну

і підставимо її у рівняння (5.18). Тоді

. (5.19)

Дослід показав, що у процесі Джоуля-Томсона і завжди. Отже, знак коефіцієнта Джоуля-Томсона визначатиметься знаком чисельника.

1. При коефіцієнт , тому . При малих відстанях між молекулами сили відштовхування між молекулами переважають над силами притягання (рис.5.1). При розширенні вони виконують роботу над молекулами газу, надаючи їм додаткову кінетичну енергію, отже газ нагрівається.

2. При коефіцієнт . У цьому випадку . При великих відстанях між молекулами переважаючими є сили притягання (рис.5.1). При розширенні газ виконує роботу проти сил притягання , отже газ охолоджується,

3. Якщо ж , то , отже і , температура газу не змінюється.

Природно із останнього випадку ввести температуру інверсії, при якій змінюється знак ефекту Джоуля-Томсона

. (5.20)

Температура інверсії залежить від типу газу та об’єму, який він займає. Користуючись поняттям температури інверсії, можна стверджувати, що при температурах, вищих за температуру інверсії, газ буде нагріватись, а при нижчих – охолоджуватись.

Більш наочно вираз для температури інверсії виглядає у зведених параметрах

Рис.5.5

. (5.21)

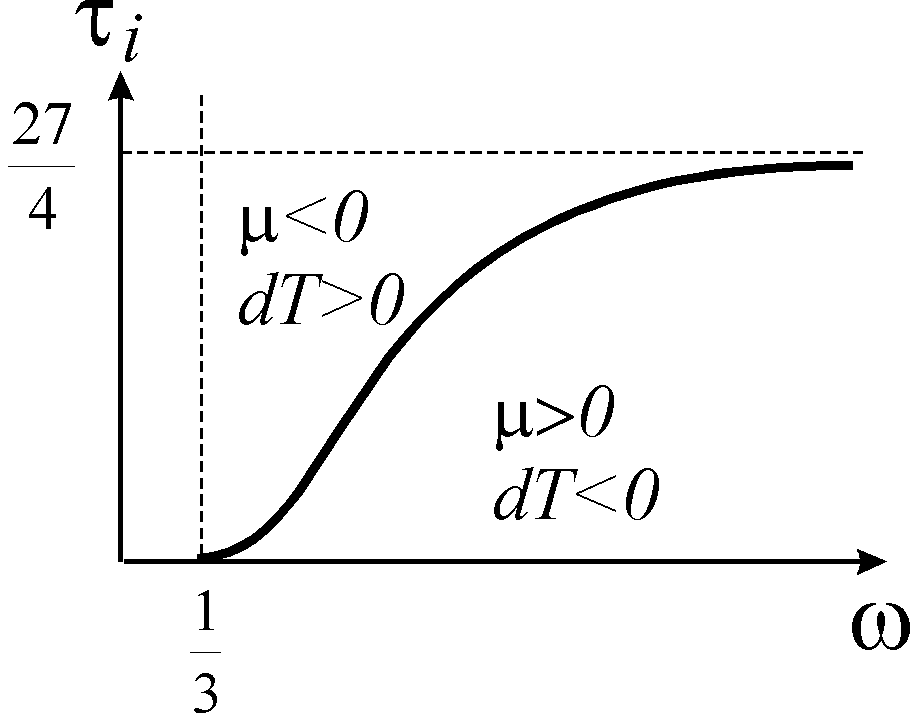
Графічно побудована залежність називається кривою інверсії (рис.5.5). Нижче кривої інверсії газ буде охолоджуватись, а вище – нагріватись.

Область значень не має фізичного змісту, оскільки ( – сумарний об’єм молекул газу). Оскільки , завжди .

Оскільки зведене рівняння Ван дер Ваальса не залежить від типу речовини, для будь-якої речовини зведена температура інверсії при .

Коли газ не дуже стиснутий, можна покласти, що та , тобто можна знехтувати об’ємом молекул порівняно з об’ємом посудини та тиском, пов’язаним із силами притягання між молекулами.

Тоді коефіцієнт Джоуля-Томсона становитиме

, (5.22)

а температура інверсії

або . (5.23)