
- •§1. Основные понятия
- •§2. Основное свойство алгебраической дроби Памятка учащимся.
- •§3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
- •§4. Сложение и вычитание алгебраических дробей с разными знаменателями
- •§5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень
- •§6. Преобразование рациональных выражений
- •§7. Функция , ее свойства и график
- •Контрольная работа.
§5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень
Умножение алгебраических дробей осуществляется по тому же правилу, что и умножение обыкновенных дробей:
![]()
Аналогично обстоит дело с делением алгебраических дробей, с возведением алгебраической дроби в натуральную степень. Правило деления выглядит так:
![]()
а правило возведения в степень
![]() Прежде
чем выполнять умножение и деление
алгебраических дробей, полезно их
числители и знаменатели разложить на
множители — это облегчит сокращение
той алгебраической дроби, которая
получится в результате умножения или
деления.
Прежде
чем выполнять умножение и деление
алгебраических дробей, полезно их
числители и знаменатели разложить на
множители — это облегчит сокращение
той алгебраической дроби, которая
получится в результате умножения или
деления.
Пример 1. Выполнить действия:
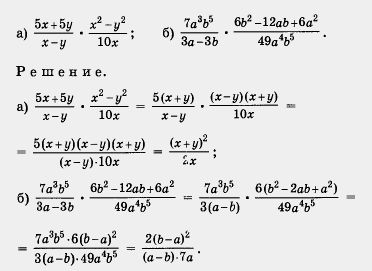 Воспользуемся
тем, что (b - а)2 =
(а - b)2.
Получим
Воспользуемся
тем, что (b - а)2 =
(а - b)2.
Получим
![]() Пp
и м е р 2.
Пp
и м е р 2.
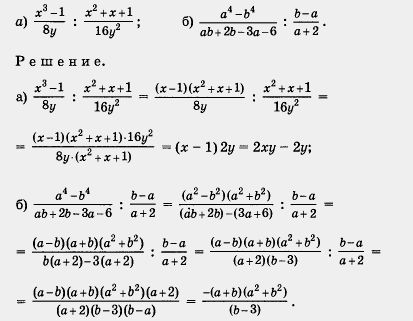 Мы
учли, что в результате деления а - b на b
- а получится -1.
Впрочем,
знак «-» в данном случае лучше переместить
в знаменатель:
Мы
учли, что в результате деления а - b на b
- а получится -1.
Впрочем,
знак «-» в данном случае лучше переместить
в знаменатель:
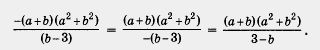 Пример
З. Выполнить
действия:
Пример
З. Выполнить
действия:
![]() Решение.
Решение.
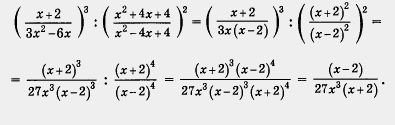
Задания по теме «Умножение дробей».
Выполните умножение: А)
 ;
Б)
;
Б)
 ;
В)
;
В)

Представьте в виде дроби: А)
 ;
Б)
;
Б)  ;
;Упростите выражение:

Задания «Деление дробей»
Выполните деление: А)
 ;
Б)
;
Б) 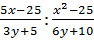 ;
В)
;
В) 
Представьте в виде дроби:

Упростите выражение:

Докажите тождество:

Упростите выражение:

§6. Преобразование рациональных выражений
Этот параграф подводит итог всему тому, что мы, начиная с 7-го класса, говорили о математическом языке, о математической символике, о числах, переменных, степенях, многочленах и алгебраических дробях. Но сначала совершим небольшой экскурс в прошлое.
Вспомните, как в младших классах обстояло дело с изучением чисел и числовых выражений.
Сначала вы изучали натуральные числа 1, 2, 3, 4, 5, ...) и операции над ними (но, конечно, этому предшествовало знакомство с цифрами). Затем появились целые числа (О, 1, -1, 2, -2, 3, -3, ...) — к ним относятся все натуральные числа, число 0 и целые отрицательные числа. Затем вы изучали рациональные числа — к ним относятся все целые числа и все дроби, как положительные, так и отрицательные. Таким образом, ко всякому натуральному числу, например к числу 2, можно «приклеить» три «ярлыка»: число 2 — натуральное, целое, рациональное. И это правильно, просто третий ярлык — рациональное число — достаточно широк, второй ярлык — целое число — поконкретнее, первый ярлык — натуральное число — самый конкретный.
Ко всякому целому числу, например к числу - 2, можно приклеить два ярлыка — целое число, рациональное число.
А,
скажем, к дроби
![]() можно
приклеить только один ярлык — рациональное
число.
можно
приклеить только один ярлык — рациональное
число.
Аналогично обстоит дело с алгебраическими выражениями: первый этап их изучения — числа, переменные, степени («цифры»); второй этап их изучения — одночлены («натуральные числа»); третий этап их изучения — многочлены («целые числа»); четвертый этап их изучения — алгебраические дроби («рациональные числа»). При этом каждый следующий этап как бы вбирает в себя предыдущий: так, числа, переменные, степени — частные случаи одночленов; одночлены — частные •случаи многочленов; многочлены — частные случаи алгебраических дробей. Между прочим, в алгебре используют иногда и такие термины: многочлен — целое выражение, алгебраическая дробь — дробное выражение (это лишь усиливает аналогию).
Продолжим упомянутую аналогию. Вы знаете, что любое числовое выражение после выполнения всех входящих в его состав арифметических действий принимает конкретное числовое значение — рациональное число (разумеется, оно может оказаться и натуральным числом, и целым числом, и дробью — это неважно). Точно так же любое алгебраическое выражение, составленное из чисел и переменных с помощью арифметических операций и возведения в натуральную степень, после выполнения преобразований принимает вид алгебраической дроби и опять-таки, в частности, может получиться не дробь, а многочлен или даже одночлен). Для таких выражений в алгебре используют термин рациональное выражение.
Пример. Доказать тождество
 Решение.
Доказать
тождество — это значит установить, что
при всех допустимых значениях переменных
его левая и правая части представляют
собой тождественно равные выражения.
В алгебре тождества доказывают различными
способами:
Решение.
Доказать
тождество — это значит установить, что
при всех допустимых значениях переменных
его левая и правая части представляют
собой тождественно равные выражения.
В алгебре тождества доказывают различными
способами:
1) выполняют преобразования левой части и получают в итоге правую часть;
2) выполняют преобразования правой части и получают в итоге левую часть;
3) по отдельности преобразуют правую и левую части и получают и в первом и во втором случае одно и то же выражение;
4) составляют разность левой и правой частей и в результате ее преобразований получают нуль.
Какой способ выбрать — зависит от конкретного вида тождества, которое вам предлагается доказать. В данном примере целесообразно выбрать первый способ.
Для преобразования рациональных выражений принят тот же порядок действий, что и для преобразования числовых выражений. Это значит, что сначала выполняют действия в скобках, затем действия второй ступени (умножение, деление, возведение в степень), затем действия первой ступени (сложение, вычитание).
Выполним преобразования по действиям, опираясь на те правила, алгоритмы, что были выработаны в предыдущих параграфах.
 Как
видите, нам удалось преобразовать левую
часть проверяемого тождества к виду
правой части. Это значит, что тождество
доказано. Однако напомним, что тождество
справедливо лишь для допустимых значений
переменных. Таковыми в данном примере
являются любые значения а и b, кроме тех,
которые обращают знаменатели дробей в
нуль. Значит, допустимыми являются любые
пары чисел (а; b), кроме тех, при которых
выполняется хотя бы одно из равенств:
Как
видите, нам удалось преобразовать левую
часть проверяемого тождества к виду
правой части. Это значит, что тождество
доказано. Однако напомним, что тождество
справедливо лишь для допустимых значений
переменных. Таковыми в данном примере
являются любые значения а и b, кроме тех,
которые обращают знаменатели дробей в
нуль. Значит, допустимыми являются любые
пары чисел (а; b), кроме тех, при которых
выполняется хотя бы одно из равенств:
2а - b = 0, 2а + b = 0, b = 0.
