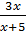- •§1. Основные понятия
- •§2. Основное свойство алгебраической дроби Памятка учащимся.
- •§3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
- •§4. Сложение и вычитание алгебраических дробей с разными знаменателями
- •§5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень
- •§6. Преобразование рациональных выражений
- •§7. Функция , ее свойства и график
- •Контрольная работа.
§3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
Алгебраические дроби с одинаковыми знаменателями складывают и вычитают по тому же правилу, что и обыкновенные дроби:
![]() т.
е. составляют соответствующую
алгебраическую сумму числителей, а
знаменатель оставляют без изменений.
т.
е. составляют соответствующую
алгебраическую сумму числителей, а
знаменатель оставляют без изменений.
Пример. Выполнить действия:
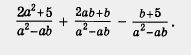 Решение.
Применив правило сложения и вычитания
алгебраических дробей, получим
Решение.
Применив правило сложения и вычитания
алгебраических дробей, получим
![]() Теперь
можно упростить числитель, выполнив
обычным образом соответствующие операции
над многочленами:
Теперь
можно упростить числитель, выполнив
обычным образом соответствующие операции
над многочленами:
(2а2 + 5) +(2аb + b) - (b + 5) = = 2а2 + 5 + 2аb + b - b - 5 = 2а2 + 2аb.
Таким
образом, заданную алгебраическую сумму
трех дробей нам удалось преобразовать
в дробь —
![]() .
А
теперь вспомните то, что мы говорили в
предыдущем параграфе: получив
алгебраическую дробь, нужно посмотреть,
нельзя ли ее сократить.
.
А
теперь вспомните то, что мы говорили в
предыдущем параграфе: получив
алгебраическую дробь, нужно посмотреть,
нельзя ли ее сократить.
Имеем
![]() Приведем
теперь решение рассмотренного примера
без комментариев (как это вы будете
делать у себя в тетрадях):
Приведем
теперь решение рассмотренного примера
без комментариев (как это вы будете
делать у себя в тетрадях):
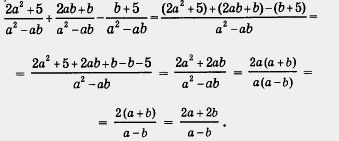 Как
видите, в результате преобразований
получилось более простое алгебраическое
выражение, чем было задано в условии
примера. Именно в упрощении и состоит
цель преобразований, поэтому часто,
вместо словосочетания «выполнить
действия», используют словосочетание
«упростить выражение».
Как
видите, в результате преобразований
получилось более простое алгебраическое
выражение, чем было задано в условии
примера. Именно в упрощении и состоит
цель преобразований, поэтому часто,
вместо словосочетания «выполнить
действия», используют словосочетание
«упростить выражение».
Задания по теме: «Сложение и вычитание алгебраических дробей с одинаковыми знаменателями»
Выполните сложение или вычитание дробей. А)
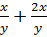 ;
Б)
;
Б) 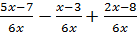 ;
В)
;
В) 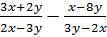
Найдите значение выражения: А)
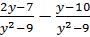 при y=3.1,
y=-2;
Б)
при y=3.1,
y=-2;
Б)
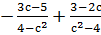 при с=3, с=-3
при с=3, с=-3
§4. Сложение и вычитание алгебраических дробей с разными знаменателями
Сложение и вычитание алгебраических дробей с разными знаменателями выполняют по тому же алгоритму, что используется для сложения и вычитания обыкновенных дробей с разными знаменателями: сначала приводят дроби к общему знаменателю с помощью соответствующих дополнительных множителей, а затем складывают или вычитают полученные дроби с одинаковыми знаменателями по правилу из § 3. Можно сформулировать алгоритм, охватывающий любые случаи сложения (вычитания) алгебраических дробей.
Алгоритм сложения (вычитания) алгебраических дробей
 Пример
1. Выполнить
действия:
Пример
1. Выполнить
действия:
![]() Решение.
Для каждой пары заданных здесь
алгебраических дробей общий знаменатель
был найден выше, в примере из § 2. Опираясь
на указанный пример, получаем:
Решение.
Для каждой пары заданных здесь
алгебраических дробей общий знаменатель
был найден выше, в примере из § 2. Опираясь
на указанный пример, получаем:
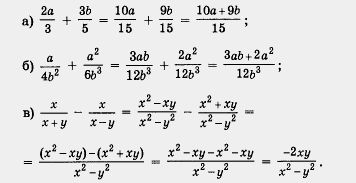 Самое
трудное в приведенном алгоритме — это,
конечно, первый шаг: отыскание общего
знаменателя и приведение дробей к общему
знаменателю. В примере 1 вы этой трудности,
может быть, не ощутили, поскольку мы
воспользовались готовыми результатами
из § 2.
Самое
трудное в приведенном алгоритме — это,
конечно, первый шаг: отыскание общего
знаменателя и приведение дробей к общему
знаменателю. В примере 1 вы этой трудности,
может быть, не ощутили, поскольку мы
воспользовались готовыми результатами
из § 2.
Чтобы
выработать правило отыскания общего
знаменателя, проанализируем пример
1.
Для дробей
![]() общий
знаменатель есть число 15 оно делится
и на 3 и на 5, является их общим кратным
(даже наименьшим общим кратным).
Для
дробей —
общий
знаменатель есть число 15 оно делится
и на 3 и на 5, является их общим кратным
(даже наименьшим общим кратным).
Для
дробей —
![]() общим
знаменателем является одночлен 12b3.
Он делится и на 4b2 и
на 6b3 ,
т. е. на оба одночлена, служащие
знаменателями дробей.
общим
знаменателем является одночлен 12b3.
Он делится и на 4b2 и
на 6b3 ,
т. е. на оба одночлена, служащие
знаменателями дробей.
Обратите внимание: число 12 — наименьшее общее кратное чисел 4 и 6. Переменная b входит в знаменатель первой дроби с показателем 2, в знаменатель второй дроби — с показателем 3. Это наибольшее значение показателя 3 фигурирует в общем знаменателе. Для дробей
![]() общим
знаменателем служит произведение (х +
у)(х - у) — оно делится и на знаменатель
х + у и на знаменатель х-у.
общим
знаменателем служит произведение (х +
у)(х - у) — оно делится и на знаменатель
х + у и на знаменатель х-у.
При отыскании общего знаменателя приходится, естественно, все заданные знаменатели разлагать на множители (если это не было подготовлено в условии). А далее следует провести работу по этапам: найти наименьшее общее кратное для числовых коэффициентов (речь идет о целочисленных коэффициентах), определить для каждого несколько раз встречающегося буквенного множителя наибольший показатель степени, собрать все это в одно произведение.
Теперь можно оформить соответствующий алгоритм.
Алгоритм отыскания общего знаменателя для нескольких алгебраических дробей
 Прежде
чем двигаться дальше, попробуйте
применить этот алгоритм к обоснованию
поиска общего знаменателя для
алгебраических дробей из примера
1.
Замечание. На
самом деле общих знаменателей для двух
алгебраических дробей можно найти
сколько угодно. Например, для
дробей
Прежде
чем двигаться дальше, попробуйте
применить этот алгоритм к обоснованию
поиска общего знаменателя для
алгебраических дробей из примера
1.
Замечание. На
самом деле общих знаменателей для двух
алгебраических дробей можно найти
сколько угодно. Например, для
дробей
![]() общим
знаменателем
может быть и число 30, и число 60, и даже
одночлен 15а2Ь. Дело в том, что и 30, и 60, и
15а2b
можно разделить как на 3, так и на 5.
Для
дробей —
общим
знаменателем
может быть и число 30, и число 60, и даже
одночлен 15а2Ь. Дело в том, что и 30, и 60, и
15а2b
можно разделить как на 3, так и на 5.
Для
дробей —
![]() общим
знаменателем, кроме найденного выше
одночлена 12b , может быть и 24b3 и
48а2b4.
Чем же одночлен 12b3 лучше,
чем 24b3,
чем 48а2b4?
Он проще (по виду). Его иногда называют
даже не общим знаменателем, а наименьшим
общим знаменателем. Таким образом,
приведенный алгоритм — это алгоритм отыскания
самого простого из общих знаменателей
нескольких алгебраических дробей,
алгоритм отыскания наименьшего
общего знаменателя.
общим
знаменателем, кроме найденного выше
одночлена 12b , может быть и 24b3 и
48а2b4.
Чем же одночлен 12b3 лучше,
чем 24b3,
чем 48а2b4?
Он проще (по виду). Его иногда называют
даже не общим знаменателем, а наименьшим
общим знаменателем. Таким образом,
приведенный алгоритм — это алгоритм отыскания
самого простого из общих знаменателей
нескольких алгебраических дробей,
алгоритм отыскания наименьшего
общего знаменателя.
Снова
вернемся к примеру 1, а. Чтобы сложить
алгебраические дроби
![]() ,
надо было не только найти общий знаменатель
(число 15), но и отыскать для каждой из
дробей дополнительные множители, которые
позволили бы привести дроби к общему
знаменателю. Для дроби
,
надо было не только найти общий знаменатель
(число 15), но и отыскать для каждой из
дробей дополнительные множители, которые
позволили бы привести дроби к общему
знаменателю. Для дроби
![]() таким
дополнительным мно-
жителем служит
число 5 (числитель и знаменатель этой
дроби умножили дополнительно на 5), для
дроби
таким
дополнительным мно-
жителем служит
число 5 (числитель и знаменатель этой
дроби умножили дополнительно на 5), для
дроби
![]() число
3 (числитель и знаменатель этой дроби
умножили дополнительно на 3).
число
3 (числитель и знаменатель этой дроби
умножили дополнительно на 3).
Дополнительный множитель есть частное от деления общего знаменателя на знаменатель данной дроби. Обычно используют следующую запись:
![]() Снова
вернемся к примеру 1,6. Общим знаменателем
для дробей
Снова
вернемся к примеру 1,6. Общим знаменателем
для дробей
![]() является
одночлен 12b3.
Дополнительный множитель для первой
дроби равен Зb (поскольку 12b3 :
4b2 =
ЗЬ),
для второй дроби он равен 2 (поскольку
12b3 :
6b3 =
2). Значит, решение примера 1,6 можно
оформить так:
является
одночлен 12b3.
Дополнительный множитель для первой
дроби равен Зb (поскольку 12b3 :
4b2 =
ЗЬ),
для второй дроби он равен 2 (поскольку
12b3 :
6b3 =
2). Значит, решение примера 1,6 можно
оформить так:
![]() Выше
был сформулирован алгоритм отыскания
общего знаменателя для нескольких
алгебраических дробей. Но опыт показывает,
что этот алгоритм не всегда бывает
понятен учащимся, поэтому мы дадим
несколько видоизмененную формулировку.
Выше
был сформулирован алгоритм отыскания
общего знаменателя для нескольких
алгебраических дробей. Но опыт показывает,
что этот алгоритм не всегда бывает
понятен учащимся, поэтому мы дадим
несколько видоизмененную формулировку.
Правило приведения алгебраических дробей к общему знаменателю

Пример 2. Упростить выражение
![]() Решение.
Первый
этап. Найдем
общий знаменатель и дополнительные
множители.
Решение.
Первый
этап. Найдем
общий знаменатель и дополнительные
множители.
Имеем 4а2 - 1 = (2а - 1) (2а + 1), 2а2 + а = а(2а + 1). Первый знаменатель берем целиком, а из второго — добавляем множитель а, которого нет в первом знаменателе. Получим общий знаменатель
a(2a - 1) (2a +1).
Удобно расположить записи в виде таблицы:

Второй этап. Выполним преобразования:
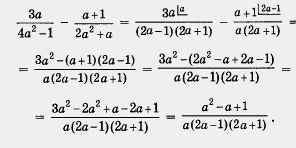 При
наличии некоторого опыта первый этап
можно не выделять, выполняя его
одновременно со вторым этапом.
При
наличии некоторого опыта первый этап
можно не выделять, выполняя его
одновременно со вторым этапом.
В заключение рассмотрим более сложный пример (для желающих).
Пример 3. Упростить выражение
![]() Решение.
Первый
этап.
Разложим
все знаменатели на множители:
Решение.
Первый
этап.
Разложим
все знаменатели на множители:
1) 2а4 + 4а3b + 2a2b2 = 2а2 (а2 + 2аb + b2) = 2а2 (а + b)2;
2) 3ab2 - За3 = За (b2 - а2) = За (b - а) (b + а);
3) 6а4-6а3b = 6а3(а- b).
Первый знаменатель берем целиком, из второго возьмем недостающие множители 3 и b - а (или a — b), из третьего — недостающий множитель а (поскольку третий знаменатель содержит множитель а3).
Алгебраические дроби
 Заметим,
что если у дополнительного множителя
появляется знак «-», то его обычно ставят
перед всей дробью, т. е. перед второй
дробью придется поменять знак.
Заметим,
что если у дополнительного множителя
появляется знак «-», то его обычно ставят
перед всей дробью, т. е. перед второй
дробью придется поменять знак.
Второй этап. Выполним преобразования:
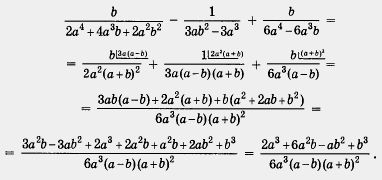 Отметим,
что замена выражения, данного в примере
3, той алгебраической дробью, которая
получилась в результате, есть тождественное
преобразование при допустимых значениях
переменных. В данном случае допустимыми
являются любые значения переменных а
и Ь, кроме a = 0, a = b, a = - b (в этих
случаях
знаменатели обращаются в нуль).
Отметим,
что замена выражения, данного в примере
3, той алгебраической дробью, которая
получилась в результате, есть тождественное
преобразование при допустимых значениях
переменных. В данном случае допустимыми
являются любые значения переменных а
и Ь, кроме a = 0, a = b, a = - b (в этих
случаях
знаменатели обращаются в нуль).
Задания по теме «СЛОЖЕНИЕ И ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ ».
Выполните сложение или вычитание дробей: А)
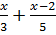 ;
Б)
;
Б) 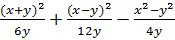 ;
В)
;
В) 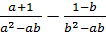
Представьте в виде дроби: А)
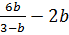 ;
Б)
;
Б) 
Докажите тождество:
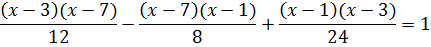
Зная, что
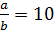 ,
найдите значение дроби:
,
найдите значение дроби: 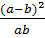
При каком значении a выражение
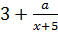 ,
тождественно равно дроби
,
тождественно равно дроби