
- •§1. Основные понятия
- •§2. Основное свойство алгебраической дроби Памятка учащимся.
- •§3. Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
- •§4. Сложение и вычитание алгебраических дробей с разными знаменателями
- •§5. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень
- •§6. Преобразование рациональных выражений
- •§7. Функция , ее свойства и график
- •Контрольная работа.
§2. Основное свойство алгебраической дроби Памятка учащимся.
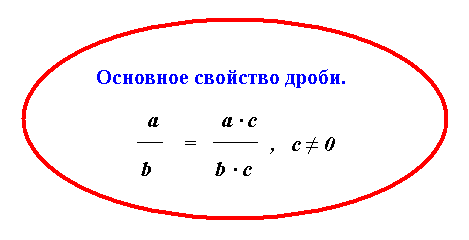

Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
Например:
![]() (и
числитель и знаменатель мы одновременно
умножили на одно и то же число 4; значение
дроби не изменилось);
(и
числитель и знаменатель мы одновременно
умножили на одно и то же число 4; значение
дроби не изменилось);
![]()
(и числитель и знаменатель мы одно временно разделили на одно и то же число 11; значение дроби не определенном смысле обобщение обыкновенной дроби; над алгебраическими дробями можно осуществлять преобразования, аналогичные тем, которые мы только что указали для обыкновенных дробей. Эти преобразования можно описать так:
1. И числитель и знаменатель алгебраической дроби можно умножить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби.
2. И числитель и знаменатель алгебраической дроби можно разделить на один и тот же многочлен (в частности, на один и тот же одночлен, на одно и то же отличное от нуля число); это — тождественное преобразование заданной алгебраической дроби, его называют сокращением алгебраической дроби.
Сформулированные
правила представляют собой основное
свойство алгебраической дроби.
Пользуясь
основным свойством алгебраической
дроби, можно дробь —
![]() заменить
(если, конечно, в этом есть необходимость)
дробью
заменить
(если, конечно, в этом есть необходимость)
дробью
![]() (числитель
и знаменатель одновременно умножили
на х - 2) или дробью
(числитель
и знаменатель одновременно умножили
на х - 2) или дробью
![]() (числитель
и знаменатель одновременно умножили
на 2х). Напротив, пользуясь основным
свойством алгебраической дроби, можно
заменить дробь
более простой дробью —
(числитель
и знаменатель одновременно разделили
на 2х, т. е. сократили дробь).
(числитель
и знаменатель одновременно умножили
на 2х). Напротив, пользуясь основным
свойством алгебраической дроби, можно
заменить дробь
более простой дробью —
(числитель
и знаменатель одновременно разделили
на 2х, т. е. сократили дробь).
Пример. Преобразовать заданные дроби так, чтобы получились дроби с одинаковыми знаменателями:
![]()
Р е ш е н и е. а) Имеем:
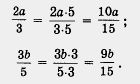 Дроби
приведены к одинаковому знаменателю
(обычно говорят «к общему знаменателю»).
Для этого пришлось числитель и знаменатель
первой дроби умножить на дополнительный
множитель 5, а числитель и знаменатель
второй дроби — на дополнительный
множитель 3; сделать это позволяет
основное свойство дроби.
Дроби
приведены к одинаковому знаменателю
(обычно говорят «к общему знаменателю»).
Для этого пришлось числитель и знаменатель
первой дроби умножить на дополнительный
множитель 5, а числитель и знаменатель
второй дроби — на дополнительный
множитель 3; сделать это позволяет
основное свойство дроби.
б) Имеем
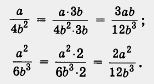 Дроби
приведены к общему знаменателю 12b3 с
помощью дополнительных множителей
соответственно 3b и 2.
в) Имеем
Дроби
приведены к общему знаменателю 12b3 с
помощью дополнительных множителей
соответственно 3b и 2.
в) Имеем
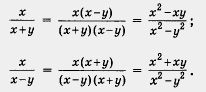 Дроби
приведены к общему знаменателю х2 -
у2 с
помощью дополнительных множителей
соответственно х - у и х + у.
Дроби
приведены к общему знаменателю х2 -
у2 с
помощью дополнительных множителей
соответственно х - у и х + у.
Приводя в этом примере алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой. Однако если при сокращении дроби мы ее упрощаем, то в рассмотренном примере каждая дробь заменялась более сложной. Наверное у вас возник вопрос: а нужно ли такое «усложняющее» преобразование?
Оказывается, нужно, и в этом мы с вами скоро убедимся.
С основным свойством алгебраической дроби связаны правила изменения знаков у числителя и знаменателя. Так, имеет место равенство
![]() здесь
числитель и знаменатель первой дроби
мы одновременно умножили на одно и то
же число - 1.
здесь
числитель и знаменатель первой дроби
мы одновременно умножили на одно и то
же число - 1.
Если же изменить знаки только в числителе или только в знаменателе, то следует изменить знак и перед дробью:
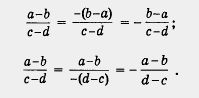
Задания: «Рациональные дроби и их свойства».
Укажите допустимые значения переменной в выражении: А)
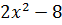 ;
Б)
;
Б)  ;
В)
;
В) 
Сократите дроби: А)
 ;
Б)
;
Б)  ;
В)
;
В)  ;
Г)
;
Г) 
Найдите значение выражения: A)
 ;
Б)
;
Б)  ;
В)
;
В) 
Вычислите: А)
 ;
Б)
;
Б) 
Найдите значение дроби:
 при a=1.8,
b=0.27
при a=1.8,
b=0.27
