§1. Основные понятия

Понятие алгебраической дроби знакомо вам из курса алгебры 7-го класса, где мы довольно много внимания уделили сокращению алгебраических дробей. Теперь настало время специально заняться изучением этого непростого раздела алгебры.

Определение. Алгебраической дробью называют выражение  , где Р и Q — многочлены; Р — числитель алгебраической дроби, Q — знаменатель алгебраической дроби.

Примеры алгебраических дробей:

Иногда алгебраическое выражение по форме является алгебраической дробью, а по существу — нет. Так обстоит дело в последних двух из пяти приведенных выше примеров. Действительно,  — это одночлен (с коэффициентом —  ); дробь  можно переписать в виде  ,а это уже не алгебраическая дробь, а многочлен (двучлен). Да и в третьем из приведенных примеров после сокращения получается не дробь, а двучлен а - 2. Но, в сущности, это не столь важно, так было и с обыкновенными дробями. Скажем,   по форме — обыкновенная  дробь, а по содержанию — натуральное число 2.

Пример 1. Найти значение алгебраической дроби

если: а) а = 2, b = 1; б) а = 5, b = 0; в) а = 4, b = 4.

Р е ш е н и е. а) При а = 2, b = 1 получаем

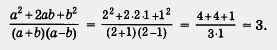б) При а = 5, b = 0 получаем

в) При а = 4, b = 4 выражение а - b обращается в нуль, а потому знаменатель данной дроби обращается в нуль. Но на нуль делить нельзя. Значит, пара значений а = 4, b = 4 является для заданной дроби недопустимой, т. е. числитель алгебраическая дробь в этом случае не имеет знаменатель смысла.

Условимся в дальнейшем, что переменные,  входящие в состав алгебраической дроби, принимают лишь допустимые значения, т. е. такие значения, при  которых знаменатель дроби не обращается в нуль.

Замечание. Пример 1 решен правильно, но «некультурно». Ведь алгебраическую дробь ,  — можно сократить. Напомним, как мы это делали в 7-м классе:

Согласитесь, что если бы мы начали с сокращения дроби, то все вычисления существенно упростились. Поэтому у математиков как бы выработался рефлекс: если им встретилась алгебраическая дробь, то прежде всего они выясняют, нельзя пи ее сократить.

Пример 2. Лодка прошла 10 км по течению реки и 6 км против течения, затратив на весь путь 2 ч. Чему равна собственная скорость лодки, если скорость течения реки равна 2 км/ч?

Решение.  Первый этап. Составление математической модели. Пусть х км/ч — собственная скорость лодки, тогда по течению реки она плывет со скоростью (х + 2) км/ч, а против течения — со скоростью (х – 2) км/ч.

По течению реки, т. Е. со скоростью (х + 2) км/ч, лодка прошла путь 10 км. Значит, время, затраченное на этот путь, выражается формулой — .  Против течения реки, т. Е. со скоростью (х – 2) км/ч, лодка прошла путь 6 км. Следовательно, время, затраченное на этот путь, выражается формулой — .  По условию задачи на весь путь (т. Е. на 10 км по течению и 6 км против течения) суммарно затрачено 2 ч. Итак, получаем

Это уравнение — математическая модель задачи.

Второй этап. Работа с составленной моделью. Обратите внимание на левую часть уравнения. Она представляет собой сумму алгебраических дробей. Таким образом, приходим к следующим выводам:

1) алгебраические дроби могут входить в состав той или иной математической модели;

2) надо научиться оперировать с алгебраическими дробями, чтобы, в частности, уметь складывать дроби   ;  3) пока мы не научимся оперировать с алгебраическими дробями, мы не сможем осуществить второй этап решения задачи — этап работы с составленной моделью.

Придется нам вернуться к этой задаче позднее, когда мы будем готовы довести ее до конца, — это произойдет в § 7.

Итак, теперь вы не сомневаетесь в том, что алгебраические дроби нужны и что мы должны научиться оперировать с ними. Этим и займемся в следующих  параграфах.