Рекомендуемая литература

1. Дмитриев В. Н., Зелинский М.М. Основы теории цепей. Конспекты лекций: – Астрахань: АГТУ, 2008. – С.55-83 и 184-188.

2. Карлащук В.И., Карлащук С.В. Электронная лаборатория на IBM PC. Том 1. Моделирование элементов аналоговых систем. - М.: СОЛОН-ПРЕСС, 2006. – С.85-180 с.

3. Теория электрической связи: Учебник для вузов/ под ред.

Д.Д. Кловского. – М.: Радио и связь, 1998. – С. 82-89.

Лабораторная работа № 3 Исследование преобразования частоты

Цель работы:

Исследование процесса преобразования частоты при использовании нелинейного элемента с квадратичным участком вольтамперной характеристики.

Решаемые задачи:

-выбор рабочей точки и рабочего участка в середине квадратичного участка ВАХ.

-настройка преобразователя на максимум АМ-сигнала на выходе при выборе наименьшей частоты гетеродина.

-настройка преобразователя на максимум АМ-сигнала на выходе при выборе наибольшей  частоты гетеродина.

-снятие характеристики преобразования частоты моногармонического сигнала.

Основные теоретические сведения

1. Преобразование частоты сигнала. В этом случае сигнал на входе устройства с переменной амплитудой и (или) фазой , сосредоточен­ный по спектру около частоты f₁ превращается на выходе устройства в сигнал , имеющий ту же форму ( К и - постоянные), но сосредоточенный по спектру около частоты .

При преобразовании частоты вверх f₂ больше, чем f_1. При преобразовании частоты вниз f₂ меньше, чем f₁.

Преобразование частоты часто используется в современных устройствах при приёме сигналов как с амплитудной, так и угловой модуляцией;

2. Преобразователь частоты. Преобразователем частоты называют устройство, позволяющее переносить спектр входного сигнала вверх или вниз по шкале частот.

В качестве преобразователя частоты может быть использован нелинейный усилитель с колебательным контуром на выходе, настроенным на специальную (комбинационную) частоту, рис. 3.1.

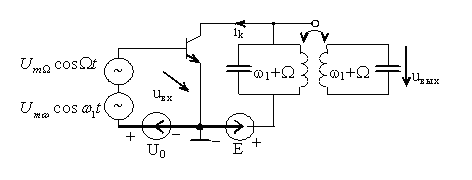
Рисунок 3.1. Схема преобразователя при преобразовании частоты вверх

Преобразование частоты вверх осуществляется путем перемножения двух колебаний и и выделения колебания с комбинационной частотой (+Ω) на выходе, следуя формуле:

cos(x)cos(y) = (1/2)[cos(x+y)+cos(x-y)]

При этом имеем:

Воздействие:

ВАХ:

Полезная реакция:

В общем случае низкочастотный сигнал можно представить в виде суммы нескольких гармонических колебаний. Для выделения полезной реакции необходим фильтр.

Преобразование частоты вниз осуществляется по той же схеме нелинейного усилителя (рис. 3.2) путем перемножения двух входных колебаний и и выделения колебания с комбинационной частотой на выходе, следуя формуле:

cos(x)cos(y) = (1/2) [cos(x+y)+cos(x-y)]

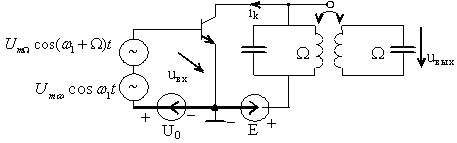
Рисунок 3.2 - Схема преобразователя при преобразовании частоты вниз

При этом имеем:

Воздействие:

ВАХ:

Полезная реакция:

В общем случае низкочастотный сигнал можно представить в виде суммы нескольких гармонических колебаний. Для выделения полезной реакции необходим фильтр низкой частоты.

3.Амплитудная модуляция ( АМ) исторически была первым видом модуляции, освоенным на практике. В настоящее время АМ применяется в основном только для радиовещания на сравнительно низких частотах (не выше коротких волн) и для передачи изображения в телевизионном вещании. Это обусловлено низким КПД использования энергии модулированных сигналов.

АМ соответствует переносу информации s(t) в амплитуду U(t) при постоянных значениях параметров несущего колебания: частоты  и начальной фазы j₀. АМ – сигнал представляет собой произведение информационной огибающей U(t) и гармонического колебания ее заполнения с более высокими частотами. Форма записи амплитудно-модулированного сигнала:

u(t) = U(t)cos( _ot+j _o), (3.1)

U(t) = U_m[1+ms(t)], (3.2)

где U_m – постоянная амплитуда несущего колебания при отсутствии входного (модулирующего) сигнала s(t), m – коэффициент амплитудной модуляции

Значение m характеризует глубину амплитудной модуляции. В простейшем случае, если модулирующий сигнал представлен одночастотным гармоническим колебанием с амплитудой S_o, то коэффициент модуляции равен отношению амплитуд модулирующего и несущего колебания m=S_o/U_m. Значение m должно находиться в пределах от 0 до 1 для всех гармоник модулирующего сигнала. При значении m<1 форма огибающей несущего колебания полностью повторяет форму модулирующего сигнала s(t), что можно видеть на рис.3.4 (сигнал s(t) = sin(_st)). Малую глубину модуляции для основных гармоник модулирующего сигнала (m<<1) применять нецелесообразно, т.к. при этом мощность передаваемого информационного сигнала будет много меньше мощности несущего колебания, и мощность передатчика используется неэкономично.

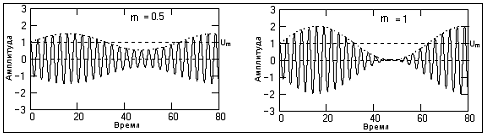Рис..3.4 – Модулированный сигнал Рис. 3.5 – Глубокая модуляция

На рис.3.5 приведен пример так называемой глубокой модуляции, при которой значение m стремится к 1 в экстремальных точках функции s(t).

Стопроцентная модуляция (m=1) может приводить к искажениям сигналов при перегрузках передатчика, если последний имеет ограниченный динамический диапазон по амплитуде несущих частот или ограниченную мощность передатчика (увеличение амплитуды несущих колебаний в пиковых интервалах сигнала U(t) в два раза требует увеличения мощности передатчика в четыре раза).

При m>1 возникает так называемая перемодуляция, пример которой приведен на рис.3.6. Форма огибающей при перемодуляции искажается относительно формы модулирующего сигнала и после демодуляции, если применяются ее простейшие методы, информация может искажаться.

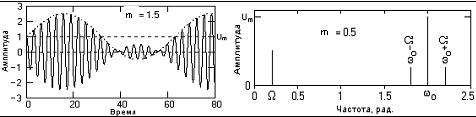
Рис. 3.6 -Перемодуляция сигнала

Рис.3.7-Физические спектры сигналов

4.Моногармоническая амплитудная модуляция. Простейшая форма модулированного сигнала создается при моногармонической амплитудной модуляции – модуляции несущего сигнала гармоническим колебанием с одной частотой Ω:

u(t) = U_m[1+m cos(Ωt)] cos(_ot), (3.3)

Значения начальных фазовых углов несущего и модулирующего колебания здесь и в дальнейшем, для упрощения получаемых выражений будем принимать равными нулю. С учетом формулы cos(x)cos(y) = (1/2)[cos(x+y)+cos(x-y)] из выражения (3.3) получаем:

u(t) = U_mcos(_ot) + (U_mM/2)cos[(_o+Ω)t] + (U_mM/2)cos[(_o- Ω)t] (3.4)

Отсюда следует, что модулирующее колебание с частотой Ωперемещается в область частоты _o и расщепляется на два колебания с частотами соответственно _o+ Ω верхняя боковая частота, и _o- j - нижняя боковая частота. Эти частоты располагаются на оси симметрично относительно частоты _{o ,} рис. 3.7. Амплитуды колебаний на боковых частотах равны друг другу, и при 100%-ной модуляции равны половине амплитуды колебаний несущей частоты. Если преобразовать уравнение (3.3) с учетом начальных фаз несущей и модулирующей частоты, то получим правило изменения фаз, аналогичное правилу изменения частоты:

-начальная фаза модулирующего колебания для верхней боковой частоты складывается с начальной фазой несущей,

- начальная фаза модулирующего колебания для нижней – вычитается из фазы несущей.

Физическая ширина спектра модулированного сигнала в два раза больше ширины спектра модулирующего сигнала.

Схема работы и измерительная аппаратура

Для работы используется универсальный стенд со сменным блоком НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ, схема которого приведена на рис. 3.8. Исследуемая цепь представляет собой преобразователь на полевом транзисторе с избирательной нагрузкой (LC-контур) в цепи стока. На затвор полевого транзистора подается сумма напряжений сигнала, гетеродина и постоянного напряжения смещения.

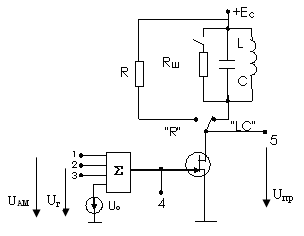
Рисунок 3.8. Схема исследуемой цепи

Для преобразования частоты используется квадратичный участок сток-затворной характеристики полевого транзистора.

Источником входного сигнала в данной работе служит внутренний генератор амплитудно-модулированных (АМ) колебаний, расположенный на левом блоке стенда ИСТОЧНИКИ СИГНАЛОВ. В этом генераторе несущая частота (195 кГц) и частота модуляции (1 кГц) фиксированы; напряжение несущей должно быть примерно 300 мВ, а глубина модуляции может изменяться в широких пределах ручкой - "m". Напряжение АМ колебания ("сигнал") с выхода внутреннего генератора должно быть подано на входное гнездо 1 исследуемой цепи.

Второй (внешний) генератор, играющий роль гетеродина, подключается к гнезду 2. Частота его колебаний выбирается в соответствии с результатами предварительного расчета равной f_Г (f_Г1 = fн – 15 кГц, f_Г2 = fн + 15 кГц), напряжение – 1 В.

В качестве измерительных приборов используeтся осциллограф. Входной сигнал наблюдается на гнезде 1, напряжение гетеродина - на зажиме 2. Для наблюдения процессов на затворе осциллограф должен быть подключен к гнезду 4; гнездо 5 служат для наблюдения и измерения выходного сигнала.