Лабораторная работа №1 Исследование преобразования формы и спектра сигналов безинерционным нелинейным элементом Цель работы:

Изучение формы и спектра сигналов на выходе резистивной цепи, содержащей безинерционный нелинейный элемент (НЭ) при моно- и бигармоническом воздействии.

Решаемые задачи:

- снятие вольтамперной характеристики (ВАХ) нелинейного элемента,

-аппроксимация ВАХ с помощью полиномиальной и кусочно-линейной функции,

-графоаналитический расчет реакции НЭ при моногармоническом воздействии,

- графоаналитический расчет реакции НЭ при бигармоническом воздействии

Основные теоретические сведения

1. Нелинейный элемент. Нелинейным элементом (НЭ) называют элемент цепи, характеризующийся нелинейной зависимостью, связывающей токи и напряжения на внешних зажимах. В данной работе в качестве НЭ используется полевой транзистор. Полевой транзистор можно полностью охарактеризовать проходной вольтамперной характеристикой (ВАХ), представляющей зависимость тока стока от напряжения затвор – исток.

2. Аппроксимация ВАХ. Аппроксимацией называют замену сложной функции приближенным аналитическим выражением.

Заданная функция в виде от дельных точек. Аппроксимирующая функция: например .

Задача аппроксимации подразделяется на два этапа:

В качестве аппроксимирующей выбирают либо полиномиальную либо кусочно-линейную функции .

Для нахождения коэффициентов аппроксимации используют либо метод интерполяции либо метод выравнивания.

3. Полиномиальная аппроксимация. Нахождение коэффициентов полиномиальной аппроксимации ВАХ поясним примером.

Пусть имеем заданную и аппроксимирующую функции.

3.1. Нахождение коэффициентов методом интерполяции.

Заданная функция

Таблица 1.1 Табличное задание функции

u	0	0,2	0,4	0,6	0,8	1,0	1,2
i	0	0,05	0,1	0,15	0.25	0.4	0.6

Аппроксимирующая функция

Метод интерполяции заключается в приравнивании двух функций в нескольких характерных точках, называемых узлами интерполяции.

3.2.. Нахождение коэффициентов методом выравнивания. Метод выравнивания заключается в преобразовании исходной аппроксимирующей функции так, чтобы получить линейную зависимость от аргумента u. Такую зависимость легко увидеть на графике, соответственно легко определить и два ее коэффициента. Например, чтобы подобрать коэффициенты аппроксимирующей функции i = a (u-U_пор)², заданную функцию i = f (u) преобразуем, взятием квадратного корня от левой и правой частей, в функцию . Соответствующая аппроксимирующая функция тоже преобразуется:

i = a (u-U_пор)²

График функции приближенно заменяем линией и находим угловой коэффициент и точку пересечения с осью абсцисс U_OT.

^{4. Кусочно-линейная аппроксимация ВАХ. Кусочно-линейная аппроксимация приближает ВАХ двумя лучами АБ и АС. После проведения этих лучей находим коэффициенты аппроксимации S и UOT}

Точка А  UOT

Луч АБ проводят так, чтобы получить наилучшее приближение при больших u (u>U_OT).

2.

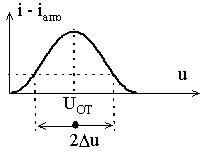
Для нелинейных преобразований интерес представляет участок излома характеристики (uUOT). Здесь выбирают рабочую точку (UO  UOT). Однако точность аппроксимации является наихудшей именно вблизи излома.

Для повышения точности расчета переменную составляющую входного сигнала выбирают значительно больше, чем величина участка наихудшего приближения ВАХ (U_m>>u),

Особенность использования кусочно-линейной аппроксимации ВАХ - большие значения переменного входного сигнала.