Рекомендуемая литература

1. Астрецов Д.В, Вострецова Е.В. ТЕОРИЯ ЭЛЕКТРОСВЯЗИ В ПРИМЕРАХ И ЗАДАЧАХ: Учебно-методическое пособие /Д.В. Астрецов, Е.В. Вострецова. Екатеринбург: ГОУ ВПО УГУ-УПИ, 2006.-С.31-36.

2. Карлащук В.И., Карлащук С.В. Электронная лаборатория на IBM PC. Том 1. Моделирование элементов аналоговых систем. - М.: СОЛОН-ПРЕСС, 2006. – С.85-180 с.

3. Теория электрической связи: Учебник для вузов/ под ред.

Д.Д. Кловского. – М.: Радио и связь, 1998. – С. 88-96.

Лабораторная работа № 6 Исследование дискретизации непрерывных сигналов во времени (теорема Котельникова) Цель работы:

Исследование процессов дискретизации и восстановления непрерывных сигналов.

Решаемые задачи:

• дискретизация сложных сигналов,

• исследование спектров исходного и дискретизированного сигналов,

• частотные и импульсные характеристики фильтров – восстановителей,

• восстановление дискретизированных сигналов.

Основные теоретические сведения

1. Дискретизация сигналов.

Дискретизация - замена непрерывных значений функции множеством ее отсчетов, совершаемых в счетные (с определенным шагом) моменты времени.

Периодическая последовательность -функций представляет собой функцию-частокол.

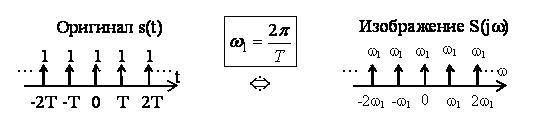
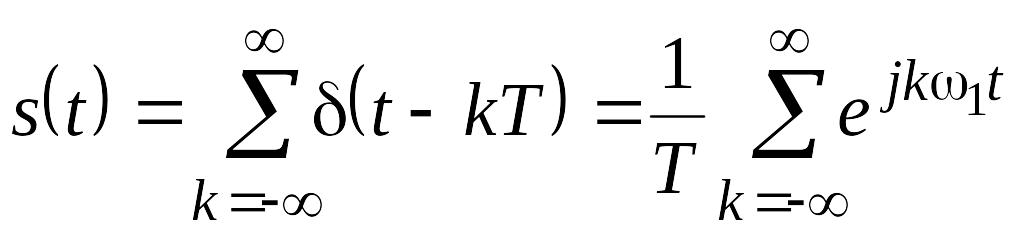
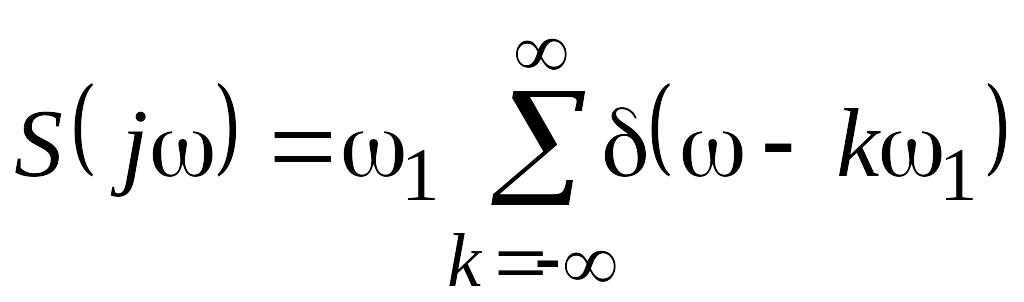
Умножение сигнала на функцию-частокол ведет к его дискретизации.

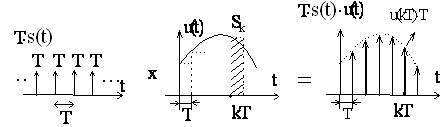
Правильно проведенная дискретизации сохраняет площадь прямоугольных импульсов, на которые разбивается сигнал шагами дискретизации. s(t)

Дискретизация сигнала в частотной области формально производятся по тем же правилам, что и во временной.

Теорема отсчетов (Котельникова). Сигнал, занимающий ограниченный спектр частот с наивысшей частотой _m, можно дискретизировать так, что новый спектр содержит не меньше информации, чем исходный спектр. При этом частота дискретизации ₁ должна удовлетворять условию:

2. Прохождение импульсов через идеальный фильтр низких частот.

Идеальный фильтр низких частот (ФНЧ) пропускает без искажений колебания частот ниже частоты среза_. : . Передаточная функция ФНЧ:

Функция Н(jω) графически представлена ниже:

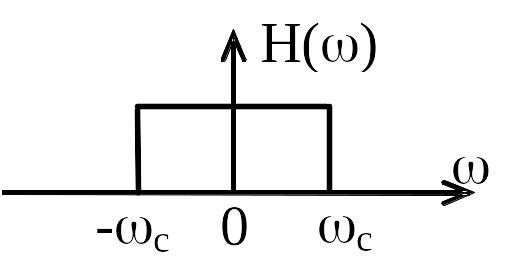
При прохождении через идеальный ФНЧ единичный импульс размывается тем больше, чем меньше частота среза f_С.

_.

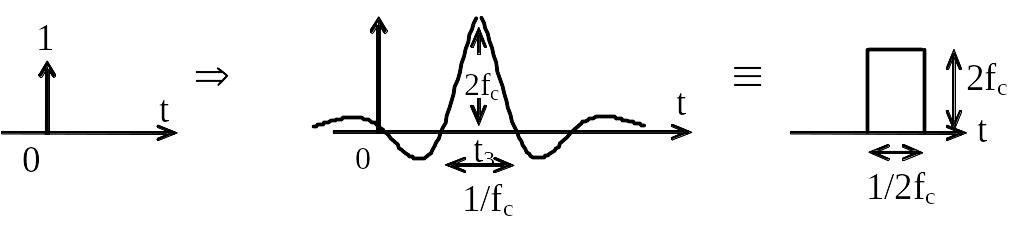
Эквивалентный по площади прямоугольный импульс имеет длительность, совпадающую с полупериодом колебаний и частотой среза. При больших f_C оба импульса могут служить приближением к дельта-функции.

При прохождении через фильтр периодической последовательности единичных импульсов происходит их размывание во временной области и уменьшение их числа в частотной.

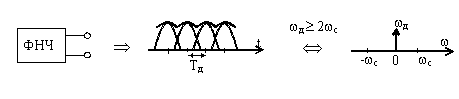
При увеличении частоты следования импульсов до величины f_c начнется сливание импульсов во временной области так, что можно отследить только огибающую их верхушек. Этому будет соответствовать один импульс в частотной области.

При выполнении условия 2fc ≤ fд действие ФНЧ на проходящие сигналы обратно действию ключа - дискретизатора.

Схема для исследования

Исследуемое устройство (рис. 6.1) размещено на сменном блоке ТЕОРЕМА КОТЕЛЬНИКОВА и представляет собой дискретизатор (обозначенный на макете как перемножитель сигналов) и набор из трех фильтров - восстановителей с разными частотами среза. Источники исследуемых сигналов - s₁, s₂ и s₃ находятся в блоке ИСТОЧНИКИ СИГНАЛОВ, а сами сигналы представляют собой гармоники с частотами 2, 4 и 6 кГц. (При необходимости исследуемый сигнал может быть усложнен добавлением еще одного гармонического сигнала с частотой 1 кГц с помощью сумматора стенда).

Р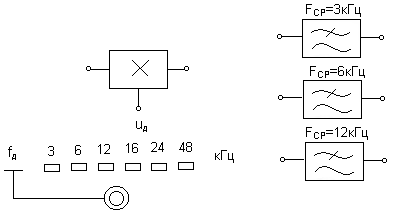 исунок 6.1- Исследуемое устройство

Дискретизатор, формирующий отсчеты s(t) непрерывного сигнала s(t), выполняет функцию перемножителя этого сигнала на короткие импульсы напряжения дискретизации (u_дискр). В данном случае дискретизатор выполнен по схеме аналогового коммутатора, пропускающего входной сигнал s(t) на выход в течение короткого времени существования импульсов дискретизации. Временной интервал между соседними отсчетами дискретизированного сигнала s(kt) зависит от выбора частоты дискретизации f_д :

Δt = 1/ f_д.

Эта частота может изменяться дискретно при нажатии кнопки f_д, при этом выбранное значение этой частоты индицируется светодиодом (f_д = 3, 6, 12, 16, 24 и 48 кГц). Все эти частоты (частоты дискретизации и частоты гармоник исследуемых сигналов) жестко синхронизированы, что упрощает наблюдение процессов на осциллографе.

В качестве фильтров - восстановителей используются три активных ФНЧ третьего порядка с частотами среза 3, 6 и 12 кГц. Для снятия импульсных характеристик фильтров используется генератор коротких импульсов "∆ - функций" (гнезда ∆(t) в блоке ИСТОЧНИКИ СИГНАЛОВ).

В соответствии с теоремой Котельникова отсчеты, следующие через интервалы времени ∆t = 1/2F_В, где F_В - верхняя частота сигнала, могут быть преобразованы в исходный сигнал после прохождения через идеальный ФНЧ с частотой среза F_СР = F_В. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза. Поэтому на практике выбирают ∆t несколько меньше, чем требуется в теореме Котельникова с тем, чтобы реальный ФНЧ с АЧХ трапециевидной формы позволял выделить спектр исходного сигнала из спектра дискретизированного сигнала, что гарантирует отсутствие искажений при обратном преобразовании (восстановлении) сигнала.

В качестве измерительных приборов используются двулучевой осциллограф и ПК, работающий в режиме анализатора спектра.