Содержание отчёта

1. Принципиальная схема преобразователя частоты. Таблица исходных и экспериментальных данных.

2. Исходная и аппроксимированная сток-затворная характеристика полевого транзистора для соответствующего варианта.

3. Осциллограммы, снятые при настройке преобразователя на максимум АМ-сигнала на выходе при выборе наименьшей частоты гетеродина. Огибающие сигналов на осциллограммах должны меняться синфазно.

4. Осциллограммы, снятые при настройке преобразователя на максимум АМ-сигнала на выходе при выборе наибольшей частоты гетеродина. Огибающие сигналов на осциллограммах должны меняться противофазно.

5. График характеристики преобразования преобразователя частоты

Контрольные вопросы

1. Какова роль полевого транзистора в схеме преобразователя частоты?

1. Какая форма ВАХ нелинейного элемента наиболее удобна для преобразования частоты?

2. Какова роль избирательной нагрузки в схеме преобразования частоты?

3. Какие требования предъявляются к нагрузке нелинейного элемента преобразователя частоты?

4. Изобразить схемы преобразователей частоты.

5. В каких устройствах и почему применяется преобразователь, транспонирующий (преобразующий) спектр сигнала?

6. Отличаются ли огибающие транспонированного и входного сигналов по форме?

7. Что такое характеристика преобразования преобразователя частоты? Как снять ее экспериментально?

8. Какую роль играют напряжение и частота гетеродина в процессе преобразования частоты?

9. Чем отличаются формы и спектры сигналов на входе и выходе преобразователя частоты?

Рекомендуемая литература

1. Дмитриев В. Н., Зелинский М.М. Основы теории цепей. Конспекты лекций: – Астрахань: АГТУ, 2008. – С. 177-188.

2. Карлащук В.И., Карлащук С.В. Электронная лаборатория на IBM PC. Том 1. Моделирование элементов аналоговых систем. - М.: СОЛОН-ПРЕСС, 2006. – С.85-180 с.

3. Теория электрической связи: Учебник для вузов/ под ред.

Д.Д. Кловского. – М.: Радио и связь, 1998. – С. 82-96.

Лабораторная работа №4 Исследование амплитудной модуляции

Цель работы:

Исследование процесса амплитудной модуляции, получение статической модуляционной характеристики и выбор оптимального режима работы модулятора.

Решаемые задачи:

- настройка генератора и колебательного контура преобразователя в резонанс.

- снятие статической модуляционной характеристики и определение по ней подходящего рабочего участка.

- снятие осциллограмм входного и выходного напряжений и определение глубины модуляции в оптимальном режиме работы модулятора.

- снятие осциллограмм при сложном сигнале, состоящем их двух гармоник.

Основные теоретические сведения

В качестве несущего колебания используется гармонический сигнал u = U_н cos(w_нt + j_н). Он характеризуется тремя параметрами: амплитудой U_н, угловой частотой w_н и начальной фазой j_н. Меняя эти параметры во времени по закону изменения первичного сигнала, получают сигналы амплитудной, частотной и фазовой модуляции (соответственно АМ, ЧМ и ФМ).

Линейная амплитудная модуляция:

Сигнал: =

= U₀ *[1+ +m b(t)] cos(w_нt +j_н) (4.1)

Где U(t)³0 – огибающая АМ сигнала;

К_АМ – крутизна характеристики модулятора;

m – индекс (глубина) модуляции;

b(t) – первичный сигнал.

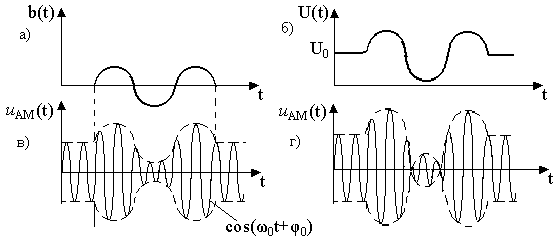
Рисунок 4.1.-Временные диаграммы при АМ

а) – первичный сигнал (отрезок синусоиды)	б) – огибающая АМ сигнала
в) – АМ сигнал при m < 1	г) - АМ сигнал при m > 1 (перемодуляция)

Глубина модуляции

Глубину амплитудной модуляции m можно определить экспериментально двумя путями:

- либо по графику амплитудного спектра модулированного сигнала, рис.4.2 ;

- либо по осциллограмме модулированного сигнала (рис.4.3).

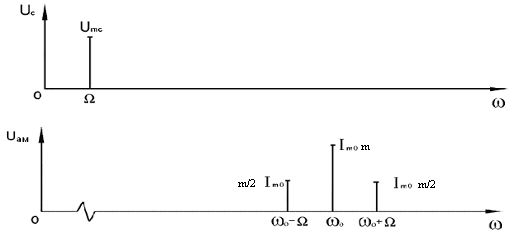
Рисунок 4.2 – Амплитудные спектры первичного и амплитудно-модулированного сигналов

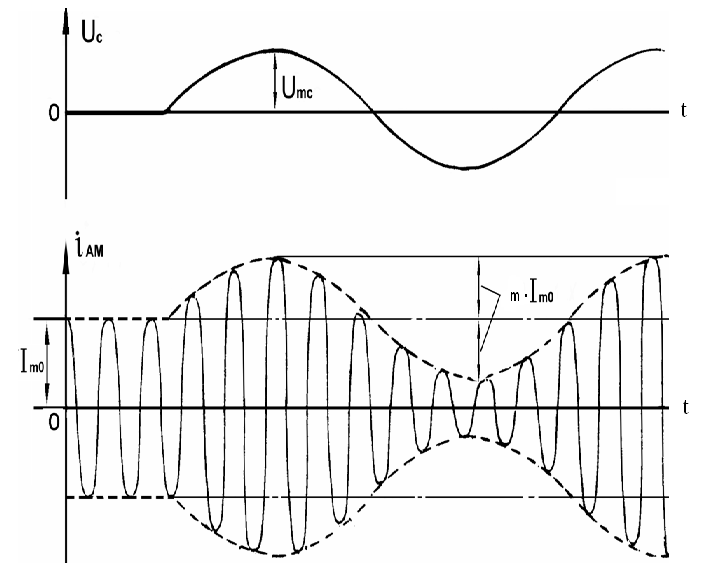
Рисунок 4.3 – Временные диаграммы первичного и амплитудно-модулированного сигналов

Модуляционная характеристика амплитудного модулятора

Зависимость меняющихся параметров несущей от первичного сигнала называют модуляционной характеристикой. В случае амплитудной модуляции модуляционная характеристика может быть представлена зависимостью амплитуды несущего колебания U_ВЫХ на выходе модулятора от напряжения смещения Е_СМ,, подаваемого на его вход.

Основу модулятора составляет нелинейный элемент (НЭ). Пусть на его вход подано гармоническое несущее колебание с заданными параметрами U_н, w_н и j_н. Тогда переменная составляющая тока на выходе НЭ определится формулой:

i = S U_н cos(w_нt + j_н).

Если крутизна S НЭ линейно зависит от напряжения смещения Е_СМ, то она будет линейно зависеть и от любого переменного сигнала b(t) на входе, т.к. напряжение смещения всегда можно представить в виде суммы постоянной и переменной составляющих:

Е_СМ = U₀ + b(t).

Линейность зависимости крутизны S от напряжения смещения Е_СМ внешне проявляется в том, что:

- модуляционная характеристика модулятора становится линейной, т.к. амплитуда входного тока пропорциональна S;

- при переменном смещении b(t) выходной ток модулятора можно представить в виде (4.1), т.е. в виде амплитудно-модулированного сигнала.

Таким образом, линейная зависимость крутизны S нелинейного элемента от напряжения смещения Е_СМ является отличительным признаком любого амплитудного модулятора. Такую зависимость можно обеспечить работой либо на квадратичном, либо на кусочно-линейном участке ВАХ нелинейного элемента. В обоих случаях работают при больших значениях амплитуды несущего колебания на входе. Поэтому вместо обычной крутизны S, определяемой касательной к ВАХ в рабочей точке, в рассмотрение вводят среднюю крутизну S_ср, определяемую линией, соединяющей две крайние точки рабочего участка.

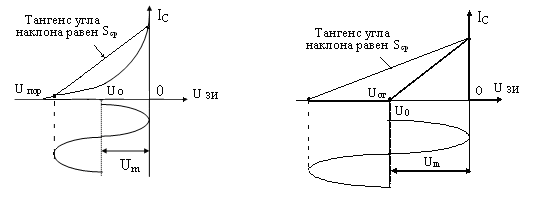
Рисунок 4.4.- Определение средней крутизны S_ср по тангенсу угла наклона линии, соединяющей крайние точки рабочего участка: а) в случае квадратичного участка б) в случае кусочно-линейного участка ВАХ.

Среднюю крутизну можно определить и по формулам:

В случае квадратичной аппроксимации при i = a (u - U_пор)² имеем:

, или S_ср =2а (U₀ - U_пор). (4.2)

В случае кусочно-линейной аппроксимации при , имеем:

, или . (4.3)

Здесь q - угол отсечки, U_m – амплитуда гармонического напряжения на входе.

Формулы (4.2) и (4.3) могут быть использованы для расчета модуляционной характеристики в виде зависимости амплитуды выходного тока I_С от напряжения смещения U₀ модулятора при постоянной амплитуде U_m гармонического напряжения на входе. Для этого следует воспользоваться формулой:

. (4.4)

Схема работы и измерительная аппаратура

В работе используется универсальный стенд со сменным блоком НЕЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ СИГНАЛОВ. Принципиальная схема исследуемой цепи приведена на рис.4.5. С помощью переключателя "R-LC" выбирается колебательный контур, а для снижения его добротности сопротивление R_Ш должно быть включено. В качестве источника несущего колебания используется встроенный генератор звуковой частоты, подключаемый ко входу 1. Источник низкочастотного модулирующего колебания с частотой 1кГц должен быть подключен ко входу 2 сумматора. Наблюдение процессов на затворе и стоке полевого транзистора осуществляется на гнездах 4 и 5 соответственно.

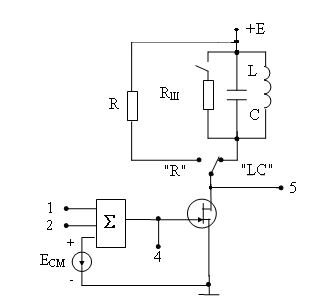
Рисунок 4.5 – Схема исследуемой цепи