Тема урока: Расчет прямоугольного сечения с одиночным армированием. Общий порядок

Цель урока: Обеспечить усвоение знаний расчетных схем с одиночным армированием.

Вопросы темы:

1.Особенности расчета железобетонных конструкций по предельным состояниям

2.Уравнение прочности нормального сечения изгибаемого прямоугольного сечения.

3.Обший порядок расчета нормального сечения.

1.Особенности расчета железобетонных конструкций по предельным состояниям

В соответствии с действующими строительными нормами железобетонные конструкции рассчитываются по методу предельных состояний.

Этот расчет гарантирует, что за период нормальной эксплуатации здания не наступит ни одно из предельных состояний.

Расчет по первой группе предельных состояний выполняют для предотвращения разрушения (расчет прочности, потери устойчивости).

Расчет по второй группе предельных состояний выполняется для предотвращения чрезмерного раскрытия трещин.

Конструкции рассчитываются по всем стадиям эксплуатации, изготовления, транспортировки. Расчет железобетонных элементов по прочности выполняются для сечений, нормальных к продольной оси, а так же наклонных к продольной оси. Сборные железобетонные элементы следует рассчитывать на воздействие усилий, возникающих при изготовлении, транспортировки и монтаже.

Расчет конструкций по предельным состояниям второй группы выполняется на действие расчетных нагрузок.

При расчете по образованию трещин проверяют условие

N N_{crc ;} М М_crc

N_crc,М_crc внутреннее усилие,которое может воспринимать сечение

N,М-усилие от внешней нагрузки

При расчете по раскрытию трещин ширина их раскрытия

2.Уравнение прочности нормального сечения изгибаемого прямоугольного сечения.

Расчет прочности нормальных сечений изгибаемых элементов прямоугольного сечения с одиночной арматурой. 1) ∑Х =0 : b * x * Rb = As Rs, отсюда X = (As Rs) / (b R_b) 2) ∑M As = 0 : M<= b R_b ( h0 – x/2) несущая способность сечения 3)∑MFb = 0 : M ≤As Rs ( h0 – x/2) для расчета в табличной форме принимаем ξ = x h₀< ξR подставим x = ξ * h₀ в (1), (2), (3) и получим: b ξ h₀ R_b = As Rs

ξ = (As Rs )/(b h₀ R_b) M≤ b ξ h₀ R_b (h_о-(ξ) h₀/2) = b ξ h₀² R_b ( 1 – ξ/2) принимаем αm = ξ(1-ξ/2) имеем: M≤αm b h₀² Rb M≤ As Rs h_о(1-ξ/2) = As Rs h₀ υ Коэффициент армирования μ = As/(b h₀) Процент армирования: μ h₀ = As/(b h₀) (b ξ h₀ Rs)/b h₀ = As Rs / (b h₀) =>

μ = ξ R_b / Rs Момент действующий на балку может воспринимается ею при разных соотношениях площади сечения арматуры и размером сечения балки, т.е. при разных значениях μ. Балку конструируют при оптимальном значении μ при котором расход материалов будет оптимальным.

Оптимальными значения для коэффициента ξ для балок находятся в пределах 0.2-0.3, для плит от 0.1- 0.2

Минимальный μ_min= 0.05 ,а максимальный процент армирования зависит от прочности бетона и определяется исходя из значений высоты сжатой зоны ξ_R. μmax = ξ_R R_b / Rs

Обычно оптимальный процент армирования μ =1-2% ,для балок и μ=0,3-0,6% для плит Рассчитывают элемент ξ = As Rs / (b h₀ R_b) ; As = ξ b h0 R_b  / R αm =M / (b h₀ 2 R_b) отсюда h₀….

As = M / ( Rs h₀υ )

3.Обший порядок расчета нормального сечения.

Определяют изгибающий момент, действующий в расчетном сечении элемента. Обычно М=ql₀²/8 (l₀- расчетный пролет балки, q- распределенная нагрузка на балку).

Принимают сечение балки (раз­меры сечения могут быть заданы).

Задаются классом прочности бетона и классом ар­матуры, чаще всего в качестве продольной рабочей арматуры при­нимается арматура класса A-III. Устанавли­вают коэффициент условия работы бетона γ_b2 (наиболее часто γ_b2 = 0,9).

Задаются расстоянием от крайнего растянутого волокна бе­тона до центра тяжести арматуры (а ≈3—5 см) и определяют ра­бочую высоту бетона

h₀ = h- а.

Находят значение коэффициента А₀:

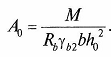
Коэффициент А₀ не должен превышать граничного значения A_0R. Если значение коэффициента А₀ > A_0R, следует увеличить сечение балки или изменить материалы.

По величине коэффициента А₀, пользуясь, опреде­ляют значения коэффициентов ξ и η.

Определяют требуемую площадь арматуры по любой из при­веденных формул:

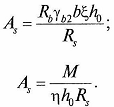
Задаются количеством стержней и определяют диаметры ар­матуры, выписывают фактическую площадь сечения подобранной арматуры.

Определяют процент армирования элемента μ и сравнивают его с минимальным процентом армирования:

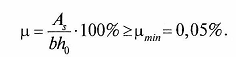
Определяют требуемую площадь монтажных стержней А'_s и по площади принимают диаметры монтажных стержней d'_s:

А'_s ≈0,1 А_s.

Определяют диаметры поперечных стержней:

d_sw ≥ 0,25 d_s.

Назначают толщину защитного слоя бетона. Конструируют сечение.

Тема урока: «Понятие прочности нормального сечения с двойной арматурой»

Цель урока: Обеспечить усвоение особенности расчета железобетонных балок с двойным армированием

1.Понятие прочности нормального сечения балок с двойной арматурой.

2.Расчет прочности нормального сечения таврового сечения с одиночным армированием

3.Определение расчетного случая.

1.Понятие прочности нормального сечения балок с двойной арматурой.

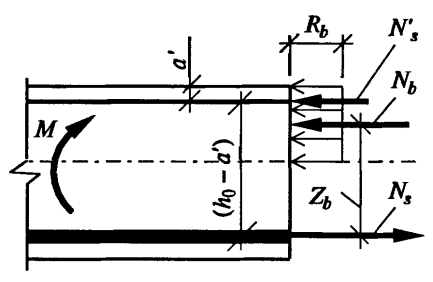
Сечение балки называется сечение с двойным армированием при наличии расчетной арматуры в сжатой зоне. Необходимость постановки расчетной арматуры в сжатой зоне бетона возникает в случае, если бетон сжатой зоны не выдерживает приходящихся на него сжимающих напряжений, а увеличивать размеры сечения элемента или прочность бетона по каким- либо причинам нельзя.

Арматура, поставленная в сжатую зону бетона, работает вместе с бетоном на сжатие, возникающее при этой схеме работы усилие в сжатой арматуре определяется как

N'_s= R _scA'_s

Следует учитывать, что арматура в сжатой зоне не так эффективна, как в растянутой зоне бетона, поэтому сечения получаются менее экономичными по сравнению с сечениями с одиночной арматурой.

Условия равновесия:

1) R_b bx +R_s A'_s = R_s A_s;

2) М- R_b bx(h₀ - 0,5х) – RscA_s'(h₀ - а') = 0.

Условия прочности:

lа) R_b bx = R_s As - R _scA'_s

2а) М ≤ R_bbx(h₀ - 0,5х)+ RscA's(ho - а').