17. Определение оператора. Понятие линейного оператора. Образ и прообраз векторов.

Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора. Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо: A(u + v) = A(u ) + A(v) , A(α·u) = α· A(u).

18. Матрица линейного оператора в заданном базисе: связь между вектором х и образом у. Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы.

Линейный оператор A действует из n-мерного линейного пространства X в m-мерное линейное пространство Y . В этих пространствах определены базисы e = {e1, ..., en} и f = {f1, ..., fm}. Пусть A(ei ) = a1i·f1 + a2i·f2 + ...+ ami·fm — разложение образа i-го базисного вектора базиса e пространства X по базису f пространства Y, i = 1, 2, ..., n. Матрицей линейного оператора в базисах e, f называется матрица A, столбцами которой являются координаты образов базисных векторов базиса e в базисе f , A = {aij}= {A(ej )i}: Координаты образа y = A(x) и прообраза x связаны соотношеннием: y = A· x,

Определение. Суммой операторов A и B называется оператор, определенный в Rⁿ на и действующий следующим образом: .Определение. Произведением оператора A на число называется оператор, определенный в Rⁿ на и действующий следующим образом: Определение. Произведением AB операторов A и B называется оператор, определенный в Rⁿ на и действующий следующим образом:

Пример:Линейные операторы A и B действуют в 3-х мерном линейном пространстве X = {x| x = (x1, x2, x3)} следующим образом: A(x) = (2x1, x2 + 5x3, − x1), B(x) = (x1− x2, x3 + x2, 0) для всех x из X.Матрицы операторов A и B имеют соответственно вид:

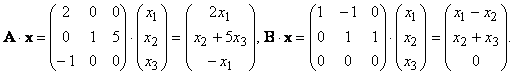
19. Собственные векторы и собственные значения оператора A ~ (матрицы А). Характеристический многочлен оператора и его характеристическое уравнение.

Определение. Ненулевой вектор x называется собственным вектором линейного оператора 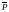, если найдется такое число λ, называемое собственным значением линейного оператора, что (x) = λ·x (1) Рассмотрим линейный оператор A, действующий в линейном пространстве X: y = A(x), ∀x ∈ X, y ∈ X. Число λ называется собственным значением оператора A, если существует такой ненулевой вектор x, что справедливо равенство A(x) = λ·x. Любой ненулевой вектор x ≠0, удовлетворяющий этому уравнению, называется собственным вектором оператора A, отвечающим собственному значению λ. A(x) = λ·x, x ≠0, x ∈ X.

Пусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei ) = λ iei, ei ≠ 0, ei ∈X.Или пусть A — матрица оператора A, или произвольная квадратноя матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. — Если λ1, λ2, ..., λn — собственные значения матрицы A, то tr A = a11+ a22+...+ ann = λ1 + λ2 + ...+ λn. — Если λ1, λ2, ..., λn — собственные значения матрицы A, то det A = λ1 · λ2 · ...· λn. — Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0. — Оператор A (матрица A) имеет не более n различных собственных значений. — Собственные значения матриц A и AT совпадают. — Если матрица A обратима, то все её собственные значения отличны от нуля, λ i≠ 0; при этом собственными значениями обратной матрицы A− 1 являются числа (λ i)− 1, а соответствующие собственные векторы совпадают. — Если число λ — собственное значение матрицы A, то собственным значением матрицы Ak является число λk , а соответствующие собственные векторы совпадают. — Собственные значения подобных матриц A и C− 1·A·C совпадают. Здесь C — невырожденная матрица. — Собственный вектор, отвечающий собственному значению λ i является ненулевым решением линейной однородной системы (A −λE)· x = 0, x≠ 0, x ∈ X. — Собственные векторы, отвечающие различным собственным значениям, линейно независимы. — Если линейный оператор A имеет n различных собственных значений, то соответствующие собственные векторы образуют базис пространства X, который называется собственным базисом линейного оператора. — Если линейный оператор имеет собственный базис, то матрица оператора в собственном базисе имеет диагональный вид; диагональными элементами являются собственные значения оператора. — Собственные векторы, отвечающие различным собственным значениям, ортогональны.

Пусть A — линейный оператор, действующий в n-мерном линейном пространстве X, λ i— собственное значение оператора A, а ei — соответствующий собственный вектор: A(ei ) = λ iei, ei ≠ 0, ei ∈X. Или пусть A — матрица оператора A, или произвольная квадратноя матрица, λ i— собственное значение матрицы A, а ei — соответствующий собственный вектор: A·ei = λ iei,ei ≠ 0, ei ∈X. Собственные значения λ i являются корнями характеристического уравнения det(A −λE) = 0.Многочлен P(λ) = − det(A − λE), из левой части характеристического уравнения, называется характеристическим многочленом матрицы A. Характеристический многочлен P(λ) = − det(A − λE) — многочлен степени n относительно λ:P(λ) = λn − an-1λn-1+ an-2λn-2+ ...+ (−1)na0.

20.Матрица линейного оператора в базисе…см 18

21. Квадратичная форма (определение). Матрица квадратичной формы.

Ранг квадратичной формы. Пример.

Определение: Квадратичной формой L(x₁,x₂,….,x_n) от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, взятых с некоторым коэффициентом:

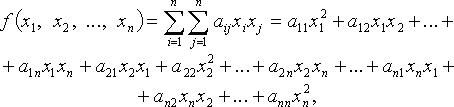
Предполагаем что коэффициенты квадратичной формы a_ij – действительные числа, причем a_ij=a_ji. Матрица A=(a_ij) (I,j= 1,2,…,n), составленная из этих коэффициентов, называется матрицей квадратичной формы. В матричной записи квадратичная форма имеет вид:L=X^’AX, где X=(x₁,x₂,…,x_n)^’-матрица-столбец переменных.

L =(x₁,x₂,x₃) (4 -6 -5) (x₁)

( -6 1 0 ) (x₂)

(-5 0 -3) (x₃)

Ранг матрицы квадратичной формы равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.