14. Векторное (линейное) пространство. Его размерность и базис. Теорема о существовании и единственности разложения вектора линейного пространства по векторам базиса.

Векторное пространство называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит. Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Совокупность n линейно независимых векторов n- мерного векторного пространства называется его базисом.

Теорема. Каждый вектор линейного n- мерного пространства можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса. Доказательство. Пусть - произвольный базис пространства и Так как любые n+1 векторов пространства линейно зависимы, то зависимы, в частности, и векторы , т.е. существуют не равные одновременно нулю числа , такие, что При этом , в противном случае хотя бы одно из чисел было бы отлично от нуля, и вектора были бы линейно зависимы. Следовательно, Полагая , будем иметь . Это представление через единственно. Доказывается от противного. Числа называются координатами вектора в базисе .

Теорема. Если - линейно независимые векторы пространства и любой вектор линейно выражается через , то эти векторы образуют базис в . Доказательство. Векторы , по условию, линейно независимы. Покажем, что в пространстве нет более чем n линейно независимых векторов. Выберем произвольные векторов из : . По условию, каждый из них можно линейно выразить через :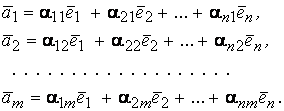 Рассмотрим матрицу: 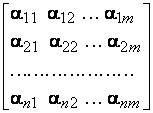Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то m столбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы . Итак, пространство n – мерно и - его базис.

15. Скалярное произведение векторов в n-мерном пространстве. Евклидово пространство. Длина (норма) вектора. Если каждой паре векторов x, y линейного пространства L поставлено в соответствие действительное число (x, y), так, что для любых x, y и z из L и любого действительного числа α справедливы следующие аксиомы:(x, y) = (y, x),(α·x, y) = α·(x, y),(x + y, z) =(x, z) + (y, z),(x, x)> 0 при x ≠ 0, (0, 0) = 0, то в пространстве L определено скалярное произведение (x, y).Если в линейном пространстве определено скалярное произведение, то такое пространство называется евклидовым пространством. Скалярным произведением векторов и в многомерном пространстве называется число Длиной n-мерного вектора называется квадратный корень из скалярного квадрата: Вектор, длина которого равна единице, называется единичным.

16. Ортогональные векторы. Ортогональный и ортонормированный базисы. Теорема о существовании ортонормированного базиса в евклидовом пространстве.

Если скалярное произведение двух ненулевых векторов x и y евклидова пространства E равно нулю, то векторы называются ортогональными векторами:(x, y) ←→ x ⊥ y. Если длина вектора равна единице, он называется нормированным вектором:(x,x) = 1, |x| = 1.Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.Если векторы системы векторов e1, e2, ..., enпопарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (ei, ej) = 0, если i ≠ j ,(ei, ei) = 1. Если e1, e2, ..., en — ортонормированная система и x = x1e1 + x2e2 + ... + xnen — разложение вектора x по этой системе, то xi =(x, ei). Ортонормированная система, состоящая из n векторов n-мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.Если e1, e2, ..., en — ортонормированный базис n-мерного евклидова пространства и x = x1e1 + x2e2 + ... + xnen — разложение вектора x по этому базису, то координаты xi вектора x в ортонормированном базисе вычисляются по формулам xi =(x, ei), i = 1, 2, ..., n. Пусть e1, e2, ..., en — ортонормированный базис n-мерного евклидова пространства и пусть x = x1e1 + x2e2 + ... + xnen , y = y1e1 + y2e2 + ... + ynen — разложения векторов x и y по этому базису.Тогда скалярное произведение векторов x и y вычисляется по формуле: (x, y) = x1· y1 + x2· y2 + ... + xn· yn . Теорема. Во всяком n-мерном евклидовом пространстве Е существует ортонормированный базис. Доказательство. Согласно определению размерности в пространстве Е найдется n линейно независимых элементов f1, f2,..., fn. Докажем, что можно построить n элементов e1,e2 ,...,en , линейно выражающихся через f1, f2,..., fn и образующих ортонормированный базис. Проведем доказательство возможности построения таких элементов e1,e2 ,...,en методом математической индукции. Если имеется только один элемент f1, то для построения элемента e1 с нормой, равной единице, достаточно нормировать элемент f1, т.е. умножить этот элемент на число , обратное его норме (напомним, что среди линейно независимых элементов f1, f2,..., fn не может быть нулевого элемента, так что норма f1 больше нуля). Мы получим при этом элемент e1 = f1 с нормой, равной единице.

Считая, что m — целое число, меньшее n, предположим, что нам удалось построить m элементов e1,e2 ,...,em, линейно выражающихся через f1, f2,..., fm, попарно ортогональных и имеющих нормы, равные единице. Докажем, что к этим элементам e1,e2 ,...,em можно присоединить еще один элемент em+1, линейно выражающийся через f1, f2,..., fm+1, ортогональный к каждому из элементов e1,e2 ,...,em и имеющий норму, равную единице. Убедимся в том, что этот элемент em+1 имеет вид em+1 = αm+1 [fm+1 - (fm+1,em),em - (fm+1,em-1),em-1 - ... - (fm+1,e1)e1] где αm+1 — некоторое вещественное число. В самом деле, элемент em+1 линейно выражается через f1, f2,..., fm+1 (в силу того, что он линейно выражается через e1,e2 ,...,em, fm+1, акаждый из элементов e1,e2 ,...,em линейно выражается через f1, f2,..., fm). Отсюда сразу же следует, что при αm+1≠ 0 элемент em+1 заведомо не является нулевым (ибо, в противном случае, являлась бы нулевым элементом некоторая линейная комбинация линейно независимых элементов f1, f2,..., fm+1 , в которой, в силу отличен от нуля коэффициент при fm+1). Далее из того, что элементы e1,e2 ,...,em попарно ортогональны и имеют нормы, равные единице, и из соотношения сразу же вытекает, что скалярное произведение (em+1, ek) равно нулю для любого номера k, равного 1, 2,..., m. Для завершения индукции остается доказать, что число αm+1 можно выбрать так, что норма элемента будет равна единице. Выше уже установлено, что при αm+1≠ 0 элемент em+1, а, стало быть, и элемент, заключенный в в квадратные скобки, не является нулевым. Стало быть, для того чтобы нормировать элемент, заключенный в квадратные скобки, следует взять число αm+1 обратным положительной норме этого, заключенного в квадратные скобки, элемента. При этом норма em+1 будет равна единице.Теорема доказана.