7. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.

Метод Гаусса решения системы n линейных уравнений с п переменными.

Идея метода Гаусса состоит в последовательном исключении неизвестных и приведении системы к ступенчатому виду. Решение системы находится из последнего уравнения методом подстановки. Преобразования над уравнениями системы заменяются аналогичные преобразования над расширенной матрицей системой.

Нужно выписать матрицу коэффициентов системы и справа приписать к ней столбец свободных членов- такая матрица называется расширенной матрицей коэффициентов системы. Затем расширенную матрицу коэффициентов нужно привести к ступенчатому виду, применяя элементарные преобразования к строкам матрицы; исходя из полученной ступенчатой матрицы выписать новую СЛУ и решить её методом последовательного исключения переменных.

Метод Гаусса — Жордана используется для решения квадратных(квадратичных)систем линейных уравнений, нахождения обратной матрицы, отыскания ранга матрицы. Метод являлся модификацией метода Гаусса. Назван в честь Гаусса и Жордана.

8. Система m линейных уравнений с n переменными. Теорема Кронекера – Капелли. Условие определенности и неопределенности любой системы линейных уравнений

Теорема Кронекера-Капелли: СЛУ совместна тогда и только тогда, если r(A) = рангу расширенной матрицы системы.

r(A) =r(A|B)

расширенной матрицей называют матрицу А+столбец свободных членов.

СЛУ называется совместной, если она имеет хотя бы одно решение и несовместной, если решений не имеет.

Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если имеет бесконечное множество этих решений.

9. Базисные (основные) и свободные (неосновные) переменные системы m линейных уравнений с n переменными. Базисное решение.

Решение СЛУ, в котором все свободные переменные = 0 называется базисным решением.

Пусть r(A)=числу r и это число <числа n, где n-число неизвестных в СЛУ, тогда

R(тут 3 волны) переменных Х1,Х2,…Хr называют базисными(основными) переменными. Остальные n-r переменных называют свободными переменными(неосновными).

10. Система линейных однородных уравнений и ее решения. Условие существования ненулевых решений такой системы.

Пусть в СЛУ свободные члены Вi=0, тогда

такую систему называют СЛОУ

СЛОУ может быть представлена в матричном виде Ax X=0, где (0-матрица столбец из 0)

Решение СЛОУ можно обозначить в виде строки: е=(Х1, Х2,…Хn)

СЛОУ всегда имеет нулевое решение. Ненулевые решения существуют в том случае, когда определитель матрицы А=0.

Пусть r(A)=r(число) и r<n (число неизвестных). Тогда система имеет r-линейно независимых решений и набор этих решений называют фундаментальной системой решений СЛОУ

11. Векторы на плоскости и в пространстве (геометрические векторы). Линейные операции над векторами (сложение, умножение вектора на число). Коллинеарные и компланарные векторы.

Величины, встречающиеся в физике, механике и других науках, можно разделить на 2 категории: скалярные (определяются числом) и векторные (определяются числовым значением и направлением).

Векторами наз-ся направленные отрезки.

А – начало В – конец

Длина вектора наз-ся его модулем.

Вектор, начало и конец которого совпадают, наз-ся нулевым.

Векторы, равные по модулю, параллельные, но направленные в противоположную сторону, наз-ся противолежащими.

Векторы, лежащие на одной или параллельных прямых, наз-ся коллинеарными.

Векторы а, в, с наз-ся компланарными, если они лежат в одной плоскости или находятся в параллельных плоскостях.

Векторы наз-ся равными, если они имеют одинаковую длину и одинаковое направление.

Векторы, длина которых равна 1, наз-ся единичными векторами.

Сложенее векторов:Пусть даны два вектора и . Приложим вектор к точке В (концу вектора ) и получим вектор Вектор 1 называется суммой векторов и и обозначается 1= + . Это нахождение суммы называется правилом треугольника.

Сумму двух неколлинеарных векторов и можно найти по правилу параллелограмма. Для этого откладываем от любой точки О векторы = и = , а затем строим параллелограмм ОАСВ Диагональ ОС параллелограмма определяет сумму:

Вычитание вектров: Разностью векторов и называется сумма вектора с вектором - , противоположным вектору

Умножение вектора на число: Произведением ненулевого вектора на действительное число называется вектор , удовлетворяющий условиям: длина вектора равна , т.е.

2. векторы и коллинеарные 3. векторы и одинаково направлены, если , и противоположно направлены, если . Произведение нулевого вектора на любое число считается (по определению) нулевым вектором: ; произведение любого вектора на число нуль также считается нулевым вектором:

Свойства линейных операций над векторами:

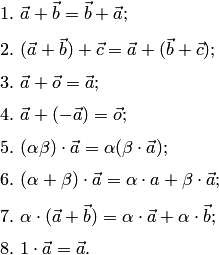
12. Скалярное произведение двух векторов (определение) и его выражение в координатной форме. Угол между векторами.

Скалярным произведением двух векторов( и ) называется число, равное произведению модулей этих векторов на косинус угла между ними. Из формулы следует, что , если - острый угол, , если - тупой угол; в том и только в том случае, когда векторы и перпендикулярны (в частности , , если или ). Скалярное произведение называется скалярным квадратом вектора и обозначается символом . Из формулы следует, что скалярный квадрат вектора равен квадрату его модуля: . Если векторы и заданы своими координатами: то их скалярное произведение может быть вычислено по формуле Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов Угол между векторами дается формулой , или в координатах Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.

13. n-мерный вектор. Линейная комбинация, линейная зависимость и независимость векторов. Упорядоченная совокупность n действительных или комплексных чисел называется n-мерным вектором. Числа называются координатами вектора. Суммой двух векторов и называется вектор, координаты которого равны сумме соответствующих координат, то есть, складывать можно только векторы количество координат которых совпадает. Произведением действительного или комплексного числа и вектора называется вектор, координаты которого равны соответствующим координатам вектора а, умноженным на то есть,

Линейная комбинация векторов Линейной комбинацией векторов e1,e2, ..., ek линейного пространства L называется выражение С1·e1+С2·e2+ ...+Сk· ek . Числа С1, С2, ..., Сk — коэффициенты линейной комбинации. Если все коэффициенты линейной комбинации С1·e1+С2·e2+ ...+Сk· ek равны нулю, то она называется тривиальной линейной комбинацией.Система e1,e2, ..., ek линейно независима, если равенство С1·e1+С2·e2+ ...+Сk· ek = 0 возможно только для тривиальной линейной комбинации.Система e1,e2, ..., ek линейно зависима, если существует нетривиальная линейная комбинация, для которой справедливо равенство С1·e1+С2·e2+ ...+Сk· ek = 0.