1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.

Понятие матрицы: матрица –прямоугольная таблица, состоящая из m строк и n столбцов.

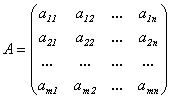
Виды матриц:

• Матрица-строка (состоит из одной строки)

• Матрица-столбец (состоит из одного столбца)

• Единичная матрица (матрица, у которой на гл. диагонали находятся единицы,а все остальные элементы=о)

Транспонирование матрицы- переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением их порядка.(соответственные строки стали столбцами)

Две матрицы одного размера называются равными, если они совпадают поэлементно.

Алгебраические операции над матрицами:

• Умножение матрицы на число.(произведение матрицы А на некоторое число К, неравное 0, называется матрица В, элементы которой =.(нужно каждый элемент умножить на это число)) К не = 0; В ij=k x aij

Справедливо обратное утверждение: общий множитель всех строк или столбцов можно выносить за знак матрицы.

• Сумма двух матриц.(алгебраической суммой двух матриц А и В называется матрица С, элементы которой соответственно =.)(матрицы одинаковых размеров складываются поэлементно)Сij = aij +(-) bij

• Умножение матриц.(произведение двух матриц А и В существует в том случае, если число столбцов матрицы А= числу строк матрицы В)Элементы матрицы С определяются по правилу: элемент сij=cумме произведений i-той строки матрицы А на j-тый столбец матрицы В(строка одного множителя, столбец от другого)

2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца.

Определитель- число, характеризующее квадратную матрицу А

Определителем матрицы 2 порядка(или определителем 2-го порядка) называется число

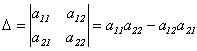
Определителем матрицы третьего порядка называется число=

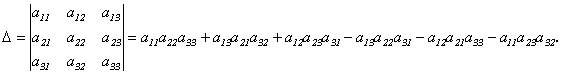
Для того, чтобы легче запомнить эту формулу, можно использовать так называемое правило треугольников. Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так: образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «-», располагаются аналогичным образом относительно побочной диагонали

Свойство 1 Определитель не изменяется при транспонировании, т.е.

 

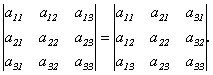
Доказательство.

 

 

=

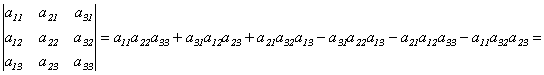
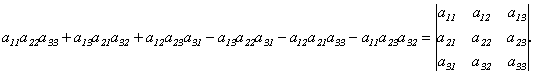
Замечание. Следующие свойства определителей будут формулироваться только для строк. При этом из свойства 1 следует, что теми же свойствами будут обладать и столбцы.

 

Свойство 2.(Если элементы какой-либо строки(столбца) умножить на одно и тоже число к, отличное от 0, то определитель увеличится в к раз) При умножении элементов строки определителя на некоторое число весь определитель умножается на это число, т.е.

.

 

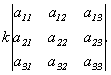Доказательство.

 

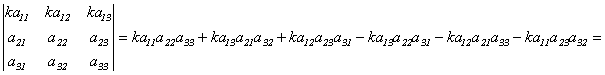
Свойство 3. Определитель, имеющий нулевую строку, равен 0.

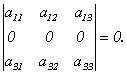
Доказательство этого свойства следует из свойства 2 при k = 0.

 

Свойство 4.(если какая-либо строка(столбец) матрицы состоит из одних 0, то её определитель =0) Определитель, имеющий две равные строки, равен 0.

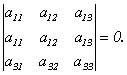
Доказательство.

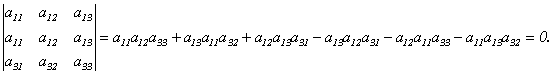
Свойство 5. (если квадратная матрица содержит 2 одинаковые строки(столбца), то её определитель = о)Определитель, две строки которого пропорциональны, равен 0.

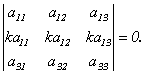
Доказательство следует из свойств 2 и 4.

 

Свойство 6. При перестановке двух строк(столбцов) матрицы определитель меняет знак на противоположный.

 

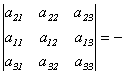
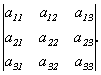
Доказательство.

 

 

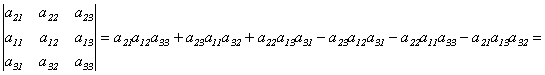
Свойство 7.

 

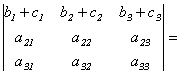
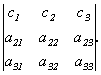
Доказательство этого свойства можно провести самостоятельно, сравнив значения левой и правой частей равенства, найденные с помощью определения 1.5(определитель 3 порядка).

 

Свойство 8. Величина определителя не изменится, если к элементам одной строки(столбца) прибавить или отнять соответствующие элементы другой строки(столбца), умноженные на одно и то же число.

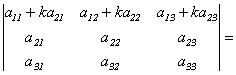
Доказательство следует из свойств 7 и 5

Теорема Лапласа: Определитель квадратной матрицы = сумме произведений элементов какой-либо строки(столбца) на их алгебраические дополнения.

где i=1,2,3.

Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат.

Найдем алгебраические дополнения к элементам первой строки:

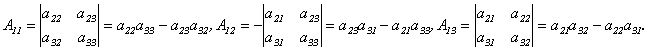
Тогда

Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.