Лекция № 3. Уравнение динамики жидкости «в напряжениях».

Водопады Игуасу на границе Бразилии и Аргентины расположены на реке Игуасу шириной 2,7 км, вода низвергается с двух базальтовых ступеней общей высотой более 70 м. Этот водопад на 20 м выше и в два раза шире Ниагарского водопада. Игуасу – каскад из 275 водопадов, разделенных скалами, покрытыми тропической растительностью. Весь поток сбрасывает вниз 1800 куб. м. воды в секунду. На моём фото- крупнейший водопад Игуасу - «Горло Дьявола» — U-образный обрыв шириной 150 и длиной 700 метров. Земля гудит и подрагивает от грохота. Голос водопада слышен за 20-25 км. Февраль 2010.

План лекции.

1. Уравнение динамики жидкости "в напряжениях"

2. Уравнение Эйлера для покоящейся жидкости.

3. Основное уравнение гидростатики, поверхности равного давления

4. Гидростатическое давление, гидростатический напор, вакуум, пьезометрическая высота

1. . Уравнение динамики жидкости "в напряжениях"

Теория гидродинамики развивалась эволюционным путём: от простого к сложному, от частного к общему. Можно сказать, что уравнение динамики жидкости начинает свою историю от второго закона Ньютона:

(1)

Если мы отнесём это уравнение к единице объёма и выразим ускорение через скорость, то уравнение (1) можно записать в виде:

(2)

где - результирующая внешняя сила, отнесённая к единице объёма.

Уравнение движения идеальной жидкости (жидкости, лишённой вязкости) впервые получил Леонард Эйлер. Когда Вы познакомитесь с уравнением Эйлера, вспомните уравнение (2).

Уравнения движе­ния вяз­кой жид­ко­сти впервые получил фран­цуз­ский учё­ный и ин­же­нер Анри На­вье. Для этого ему по­тре­бо­ва­лось вве­сти тен­зор на­пря­же­ний, то есть учесть не толь­ко нормаль­ные си­лы, но и каса­тель­ные си­лы давления жидкости. В пра­вую часть урав­не­ния На­вье ввёл до­пол­ни­тель­ный член, от­вет­ствен­ный за про­яв­ле­ние вяз­ко­сти.

Нам удобнее не повторять историю гидродинамики, а применить принцип «от общего к частному». Мы познакомимся с выводом наиболее общего уравнения движения жидкости, известного под названием «уравнение динамики жидкости «в напряжениях», а из него в качестве частных случаев, получим уравнения Эйлера для покоящейся жидкости, уравнения Эйлера движения идеальной жидкости, уравнение Эйлера в форме Громеко-Ламбе, уравнение Навье-Стокса.

Вывод уравнения динамики жидкости «в напряжениях» выполним, используя теорему об изменении главного вектора количества движения.

Применительно к механике жидкости и газа эта теорема формулируется следующим образом:

производная по времени от главного вектора количества движения жидкости в объёме контрольного элемента равна главному вектору внешних массовых и поверхностных сил, приложенных соответственно к частицам контрольного элемента внутри него и на ограничивающей его поверхности.

(3)

Здесь - главный вектор количества движения, - главный вектор внешних массовых сил, - главный вектор поверхностных сил.

А нри Навье (1785—1836) — французский инженер и учёный. В 1802 году Навье поступил в политехническую школу, а в 1804 продолжил свое обучение в Национальной школе мостов и дорог, которую закончил в 1806 году. Он руководил строительством мостов в городах Франции, а также построил пешеходный мост на Остров Сите в Париже, был главным инспектором в Корпусе мостов и дорог. В 1824 году Навье принят во Французскую Академию наук. В 1830 зачислен на должность профессора в Национальной школе мостов и дорог, а в следующем году сменил на посту профессора математики и механики Коши в Политехнической школе. Автор ряда трудов по строительной механике, сопротивлению материалов, теории упругости, гидравлике и гидромеханике. Автор курса сопротивления материалов. Навье сформулировал теорию упругости в математическом виде (1821 г.), сделав её пригодной для применения в строительстве с достаточной точностью. Его основной вклад (1822) – уравнение движения вязкой жидкости, играющее ключевую роль в гидродинамике (уравнение Навье-Стокса).

Вывод уравнения динамики жидкости «в напряжениях».

Выделим в потоке жидкости контрольный элемент жидкости произвольных размеров и формы, находящийся под действием внешних объёмных сил (например, сил гравитации) и под действием поверхностных сил (сил давления жидкости на поверхности контрольного элемента со стороны внешних частиц жидкости).

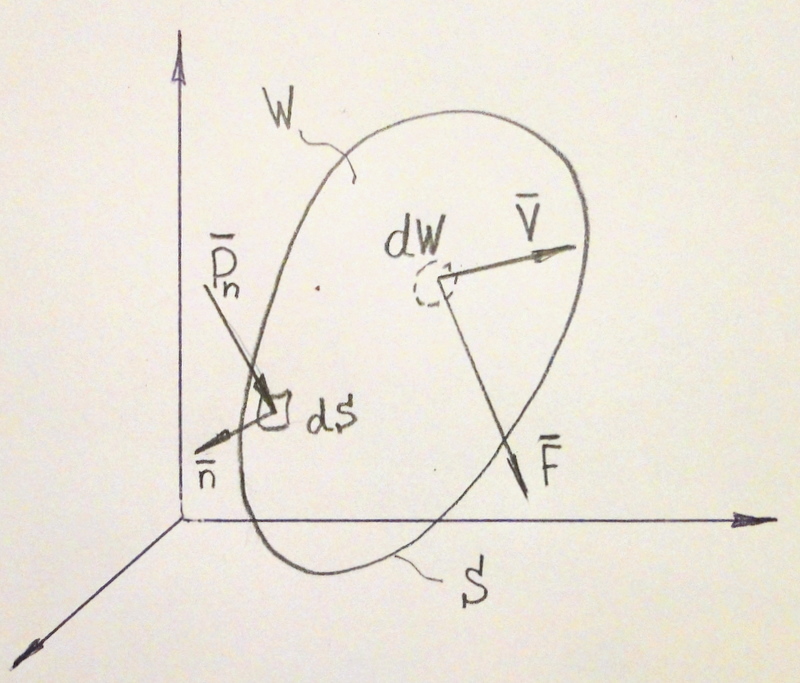Главный вектор количества движения жидкости в объёме , ограниченном поверхностью , может быть вычислен следующим образом:

Главный вектор массовых сил в объёме :

Главный вектор поверхностных сил , действующих на поверхности :

Подставив выражения , и в уравнение (3), получим:

(4)

Преобразуем левую часть уравнения (4), помня о том, что:

- результат вычисления производной по времени от пространственного интеграла не зависит от последовательности действий – знак производной можно внести под знак интеграла;

- производная по времени от массы контрольного элемента равна нулю – масса остаётся неизменной в течение всего периода наблюдений.

(5)

Воспользуемся уравнением (32) из конспекта лекции № 2

и подставим это выражение во второй интеграл правой части уравнения (4). После этого применим формулу Остроградского (см. уравнение (21) из конспекта лекции № 2):

(6)

Объединим пространственные интегралы в уравнениях (4,5,6) и перенесём их в левую часть уравнения:

(7)

В силу произвольности выбора формы и размеров контрольного элемента , то-есть в силу произвольности области интегрирования, равенство пространственного интеграла (7) нулю означает равенство нулю подынтегральной функции всюду в этой области. Отсюда мы получаем уравнение динамики жидкости «в напряжениях»:

(8)

Другие формы представления этого уравнения:

или (9)

В дальнейшем нам потребуется развёрнутая форма уравнения динамики жидкости «в напряжениях» в проекциях на оси координат. Воспользуемся для этого уравнениями (18) из лекции № 1

(10)

Здесь через обозначены проекции вектора скорости на оси координат, причём,

(11)

а результирующий вектор объёмных сил имеет проекции на оси координат :

С учётом сделанных замечаний уравнение динамики жидкости «в напряжениях» в проекциях на оси координат представим в виде:

(12)

(13)

(14)

Уравнение динамики жидкости «в напряжениях» вместе с уравнением неразрывности составляют основу математической модели механики жидкости.