3. Уравнение неразрывности в дифференциальной форме.

Напомню, что плотность жидкости – это скалярная величина, определяемая как предел отношения массы жидкости к её объёму, когда объём стягивается в точку.

Следовательно, (1)

Рассмотрим контрольный элемент жидкости , состоящий в любой момент времени из одних и тех же частиц жидкости. Масса такого элемента в Ньютоновской механике сохраняет свою величину постоянной. Поэтому для контрольного элемента справедливо:

(2)

Заменим в уравнении (2) выражение и раскроем производную произведения двух величин:

(3)

Вычислим приращение объёма контрольного элемента жидкости через скорости. Рассмотрим контрольный элемент в форме прямоугольного параллелепипеда со сторонами . Его объём в момент времени равен

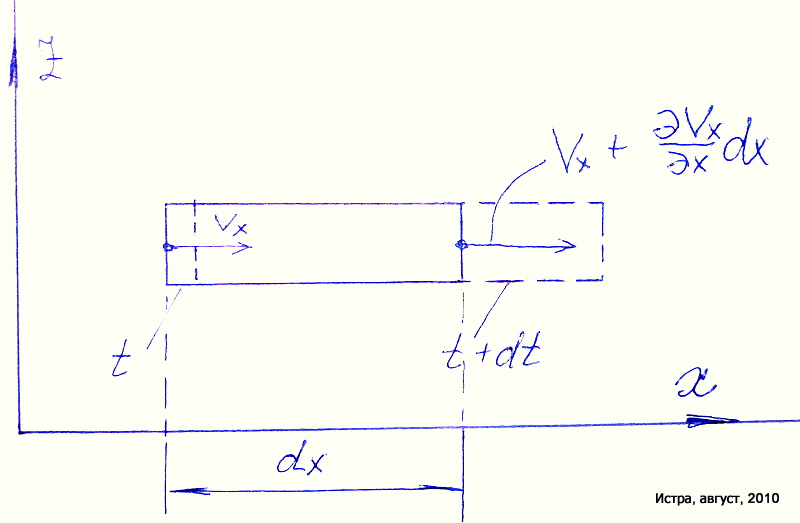(4)

За время каждая грань контрольного элемента переместится на некоторое расстояние, вследствие чего объём изменится. Левая грань, параллельная плоскости , перемещается вдоль оси со скоростью . Правая грань, параллельная этой же плоскости , перемещается со скоростью . (Вспомните разложение функции в ряд Тэйлора: )

Соответственно, этими гранями за промежуток времени будут пройдены расстояния и .

В момент времени длина контрольного элемента в направлении оси станет равной

(5)

Аналогично, вдоль других осей:

(6) (7)

В момент времени объём контрольного элемента будет равен:

(8)

Приращение объёма контрольного элемента за время равно разности объёмов в моменты времени и :

(9)

Р аскроем скобки в выражениях (8,9) и расположим слагаемые по степеням :

Произведём сокращения и, пренебрегая бесконечно малыми более высокого порядка ( ), получим:

Или, поделив на ,получим:

(10)

Подставив в (3) выражение (10) и поделив на , получим уравнение неразрывности в дифференциальной форме:

(11)

Вы можете встретить уравнение неразрывности с использованием других общепринятых обозначений, например,

, (12)

где дивергенция скорости равна:

(13)

или

(14)

где символом обозначен оператор набла (оператор Гамильтона), который определяется следующим образом:

(15)

где - единичные векторы по осям .

Равенство

(16)

получают символьно, формально применяя к векторам правила вычисления скалярного произведения двух векторов

(17)

Получим более распространённую, но столь же общую форму уравнения неразрывности. Вспомним выражение полной производной по времени от функции четырёх переменных:

(18)

Или заметив, что получим полезное выражение:

(19)

Раскроем уравнение (11), используя выражение (19) и перегруппируем слагаемые, как это показано ниже:

(20)

Или

(21)

Или

(22)

Или

(23)

Частные случаи уравнения неразрывности.

1. Установившееся движение жидкости – движение, при котором в любой точке все физические величины остаются постоянными в течение всего времени наблюдения; в установившемся режиме движения частная производная от плотности по времени равна нулю. Уравнение неразрывности в пространстве в установившемся режиме принимает вид:

(24)

или

(25)

или

(26)

2. Уравнение неразрывности для несжимаемой жидкости ( ) в пространстве:

(27)

или

(28)

Отметим, что уравнения (27, 28) верны и для установившегося и для неустановившегося режимов течения.

3. Уравнение неразрывности для плоского движения несжимаемой жидкости ( ):

(29)

4. Уравнение неразрывности для одномерного движения несжимаемой жидкости ( ), например, вдоль оси 0х, (или вдоль другого направления):

(30)

Следовательно, из уравнения неразрывности следует, что в этом виде движения в любой момент времени во всех точках трубопровода постоянного диаметра скорость жидкости одинакова. Ответьте теперь на такой вопрос. Пусть на начальном конце действующего водопровода длиной более километра перекрывают наполовину кран, уменьшая тем самым подачу воды в водопровод. Как быстро изменится расход воды в конце водопровода?

Значение и применение уравнения неразрывности.

1. Уравнение неразрывности является одним из основных фундаментальных уравнений, незаменимой составляющей математической модели механики жидкости и газа. В этом главное его значение.

2. Уравнение неразрывности может быть использовано для проверки корректности уравнений, описывающих поле скоростей, полученных, например, экспериментальным путём.

Пример: Соблюдается ли уравнение неразрывности для потока несжимаемой жидкости, если поле скоростей задано следующим образом:

Ответ: да

3. Уравнение неразрывности может быть использовано для вычисления одной из компонент вектора скорости, если заданы остальные.

Пример: Для установившегося плоского движения несжимаемой жидкости известно:

и вдоль оси Ох

Найти выражение для скорости и модуль скорости в точке (-1,1).

Ответ:

4. Уравнение неразрывности может использоваться для уточнения экспериментальных коэффициентов в аппроксимационных формулах поля скоростей.

Пример: В эксперименте коэффициент А найден равным 2.4 При каком значении коэффициента A эмпирические уравнения поля скоростей удовлетворяют уравнению неразрывности ?

Ответ: А = 2,41

5. Уравнение неразрывности может быть использовано для сокращения необходимого объёма экспериментов по определению поля скоростей.

Пример. Докажите, что для экспериментального определения поля скоростей при установившемся плоском движении несжимаемой жидкости достаточно найти, например, зависимости и , а искать экспериментально не обязательно.

Пусть , а вдоль оси Ох . Найти

Ответ:

Конец лекции № 1