
- •Лекция № 14. Закон трения Стокса
- •1. Закон трения Стокса (обобщённый закон трения Ньютона).
- •2. Вывод закона Стокса в главной системе координат.
- •3. Вывод закона Стокса в произвольной системе координат.
- •Соотношения координат при повороте осей координат.
- •Соотношение напряжений в главной и произвольной системах координат.
- •Вывод закона трения Стокса в произвольной системех координат.
- •Конец лекции № 14
Соотношение напряжений в главной и произвольной системах координат.
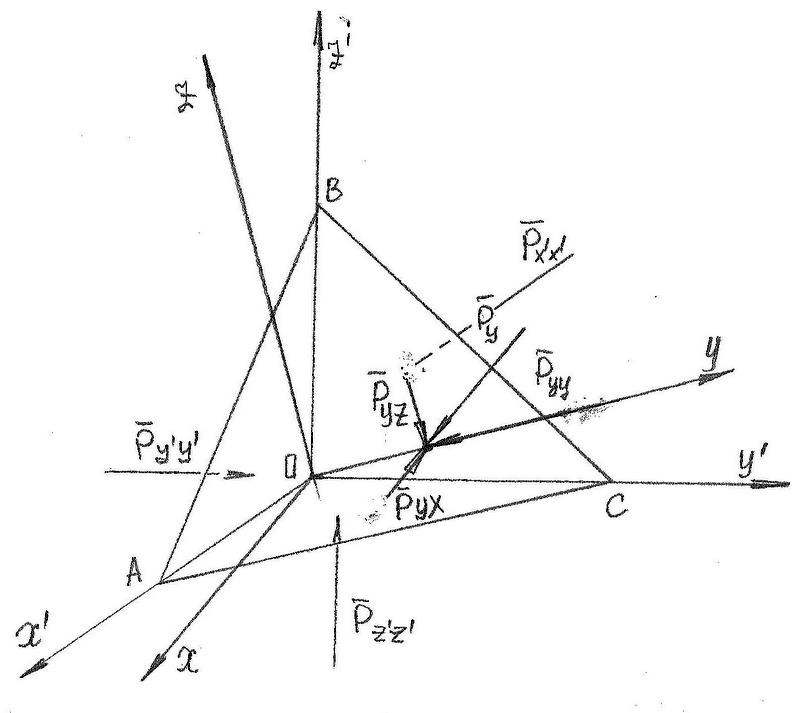
Рассмотрим
главную систему координат (![]() )
в точке 0 и произвольную систему координат
(
)
в точке 0 и произвольную систему координат
(![]() )
в этой же точке. Проведём плоскость,
перпендикулярную оси
)
в этой же точке. Проведём плоскость,
перпендикулярную оси
![]() ,
и рассмотрим тетраэдр АВС0.
,
и рассмотрим тетраэдр АВС0.
Как было показано на предыдущих лекциях, при стремлении объёма тетраэдра к нулю массовыми силами можно пренебречь в сравнении с поверхностными.
Применим принцип Д’Аламбера, согласно которому сумма всех сил, действующих на частицы тетраэдра, и сил инерции равна нулю. В проекции на ось 0y, отбрасывая слагаемые с массовыми силами, получим следующее уравнение:
![]() (94)
(94)
Мы уже отмечали на прошлых лекциях, что
![]() ,
,
![]() ,
,
![]() (95)
(95)
Подставим (95) в (94):
![]() (96)
(96)
Повторив все выкладки для площадок АВС, перпендикулярных осям 0x и 0z:
![]() (97)
(97)
![]() (98)
(98)
Применим принцип Д’Аламбера к проецированию сил на ось 0х:
![]() (99)
(99)
Произведём
сокращение на
![]() :
:
![]() (100)
(100)
Повторив все выкладки для площадок АВС, перпендикулярных осям 0x и 0z:
![]() (101)
(101)
![]() (102)
(102)
Вывод закона трения Стокса в произвольной системех координат.
Используем в уравнении (97) закон трения Стокса в главной системе координат – заменим нормальные напряжения их зависимостями от деформаций по уравнениям (36-38):
 (103)
(103)
Уравнение (103) легко упрощается, если принять во внимание, что сумма квадратов косинусов (52-57) равна 1.

Кроме того, используем уравнение (74) и (93) и повторим всё для (96) и (98) :
![]() (104)
(104)
![]() (105)
(105)
![]() (106)
(106)
Уравнения для касательных напряжений в произвольной системе координат получим, использовав уравнения (100-102) и (36-38):
 (107)
(107)
Уравнение (107) легко упрощается, если принять во внимание, что сумма попарных произведений косинусов (46-51) равна нулю. Следует принять во внимание также уравнения (90), (91) и (92).
 (108)
(108)
или, учитывая также уравнения (77-79) и (90-92) и повторив всё для (101) и (102):
 (109)
(109)
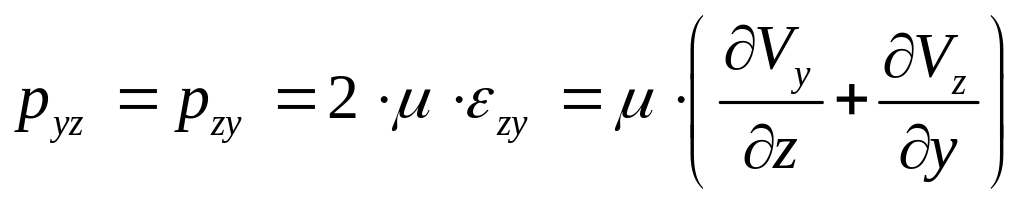 (110)
(110)
![]() (111)
(111)
Уравнения (104,105,106, 109,110,110) и есть закон трения Стокса в произвольной системе координат.
Конец лекции № 14
