
- •Лекция № 14. Закон трения Стокса
- •1. Закон трения Стокса (обобщённый закон трения Ньютона).
- •2. Вывод закона Стокса в главной системе координат.
- •3. Вывод закона Стокса в произвольной системе координат.
- •Соотношения координат при повороте осей координат.
- •Соотношение напряжений в главной и произвольной системах координат.
- •Вывод закона трения Стокса в произвольной системех координат.
- •Конец лекции № 14
3. Вывод закона Стокса в произвольной системе координат.
Обратите внимание: закону трения Стокса в главной системе координат соответствуют три уравнения – зависимости нормальных напряжений от скоростей относительных линейных деформаций, три напряжения от трёх скоростей деформаций.
В произвольной системе координат в общем случае закон трения Стокса должен будет отображать зависимость уже шести напряжений от шести скоростей деформаций. Для того, чтобы получить закон трения Стокса в общем виде, достаточно в уравнениях (36-38) заменить координаты и величины в главной системе координат на аналогичные величины в произвольной системе координат. Иными словами, нам нужно иметь соотношения для координат, скоростей, напряжений, скоростей относительных линейных и угловых деформаций в системах координат, которые можно совместить простым поворотом осей координат.
Соотношения координат при повороте осей координат.
Обозначим направляющие косинусы главных осей координат следующим образом:
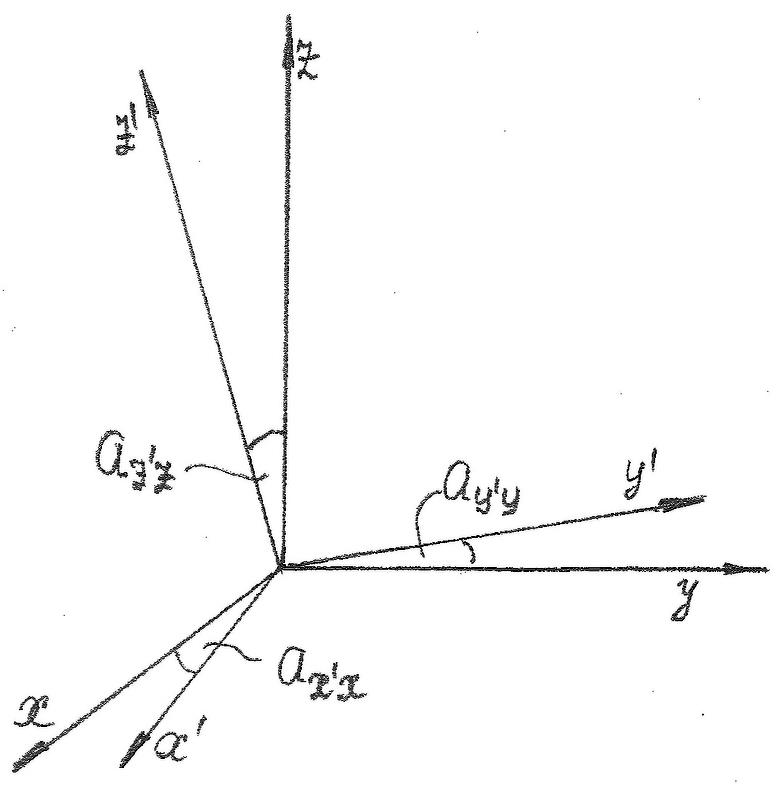
![]()
Тогда нужные нам соотношения можно записать так:
![]() (39)
(39)
![]() (40)
(40)
![]() (41)
(41)
и
![]() (42)
(42)
![]() (43)
(43)
![]() (44)
(44)
Учтём, что орты систем координат связаны соотношениями:
![]()
![]()
Свойства скалярного произведения позволяют получить несколько соотношений, которые потребуются нам чуть позже. Из равенств
![]() (45)
(45)
следует:
![]() (46)
(46)
![]() (47)
(47) ![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50) ![]() (51)
(51)
Из равенств
![]()
следует:
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
Маленький секрет. Как не перепутать индексы в этих простых и важных соотношениях ?
Я с самого начала нарисовал «шпаргалку», которой всё время пользовался, вот она:
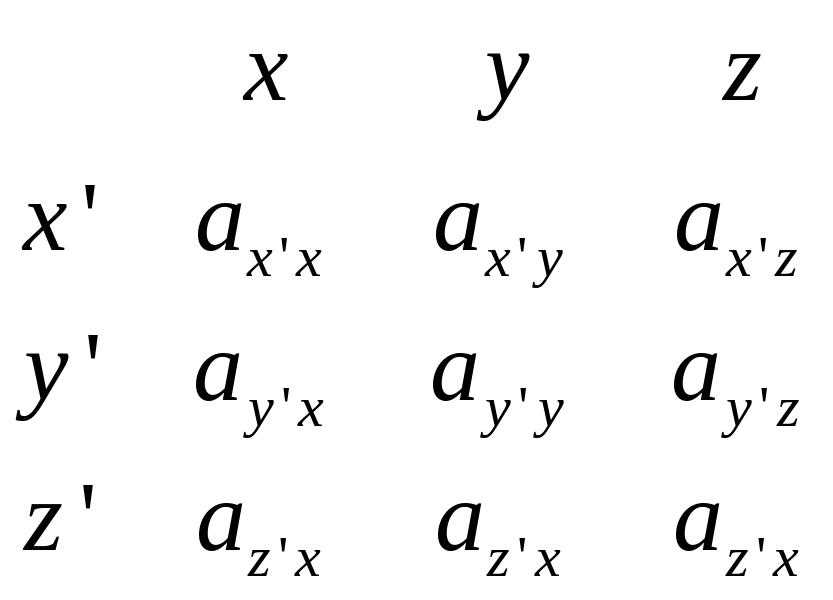 (58)
(58)
Запомнить, как построена «шпаргалка», нетрудно, а как пользоваться ею, я показывал на своём примере. Далее она нам снова пригодится.
Соотношение скоростей в главной и произвольной системах координат.
Искомые соотношения можно получить из соотношений (39-44), используя определение скорости:
![]() (59)
(59)
Дифференцируя соотношения (39-44) по времени, получаем:
![]() (60)
(60)
![]() (61)
(61)
![]() (62)
(62)
и
![]() (63)
(63)
![]() (64)
(64)
![]() (65)
(65)
Соотношение скоростей относительных линейных деформаций в главной и произвольной системах координат.
Прежде всего, отметим, что в главной системе координат угловые деформации отсутствуют, и, следовательно,
![]() (66)
(66)
Напомним, что проекции скорости на оси координат являются сложными функциями независимых переменных и справедливо выражение:
![]() (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
Отметим, что
![]() (70)
(70)
Продифференцируем
уравнение (63) трижды: по
![]() ,
по
,
по
![]() и по
и по
![]() :
:
![]() (71)
(71)
![]() (72)
(72)
![]() (73)
(73)
Подставим в уравнение (67) выражения (71-73) :
![]() (74)
(74)
Повторив предыдущие выкладки с уравнениями (64) и (65), получим:
![]() (75)
(75)
![]() (76)
(76)
Соотношение скоростей угловых деформаций в главной и произвольной системах координат.
На лекции № 5 мы познакомились с понятием скорости угловой деформации. В произвольной системе координат мы получили следующие выражения:
![]() (77)
(77)
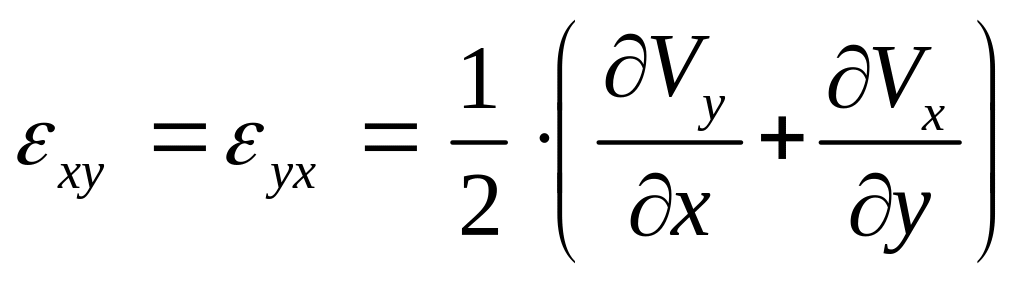 (78)
(78)
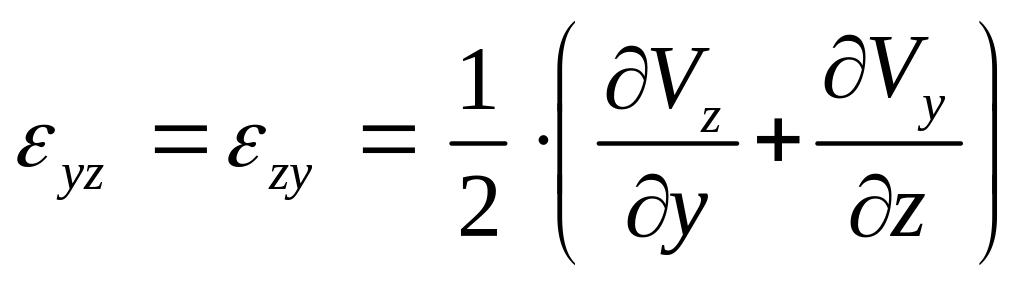 (79)
(79)
Аналогично
тому, как мы получили формулу (67), вычислим
частную производную от
![]() по
по
![]() :
:
![]() (80)
(80)
Продифференцируем уравнение (64) трижды: по , по и по с учётом (70):
![]() (81)
(81)
![]() (82)
(82)
![]() (83)
(83)
Подставим в уравнение (80) выражения (70, 81-83) :
![]() (84)
(84)
Повторим
выкладки (80-84) для частной производной
от
![]() по
по
![]() :
:
![]() (85)
(85)
Дифференцируем уравнение (65) трижды: по , по и по с учётом (70):
![]() (86)
(86)
![]() (87)
(87)
![]() (88)
(88)
Подставим в уравнение (85) выражения (70, 86-88) :
![]() (89)
(89)
Подставим в уравнение (79) выражения из уравнений (84) и (89) :
![]() (90)
(90)
И аналогично:
![]() (91)
(91)
![]() (92)
(92)
Отметим, что сложив уравнения (74-76) и используя равенства (52-54), имеем:
![]() (93)
(93)
