Лекция № 14. Закон трения Стокса

План лекции

1. Закон трения Стокса (обобщённый закон трения Ньютона).

2. Вывод закона Стокса в главной системе координат.

3. Вывод закона Стокса в произвольной системе координат.

1. Закон трения Стокса (обобщённый закон трения Ньютона).

Джордж Габрие́ль Стокс (1819 —1903) — английский физик-теоретик, математик ирландского происхождения. Работал в Кембриджском университете в должности профессора, заведующего кафедрой математики (как и Исаак Ньютон), внёс значительный вклад в гидро- и газодинамику, оптику и математическую физику, президент Лондонского королевского общества, член парламента Англии от Кембриджского университета, член Военно-медицинской Академии Петербурга. Лекции Стокса оказали чрезвычайно сильное влияние на формирование Максвелла как учёного. Кстати, Максвелл не пропустил ни одной лекции Стокса. Джордж Габрие́ль Стокс был увлекающимся человеком, высочайшим профессионалом в математике. Закон трения Стокса, гипотеза Стокса – его фундаментальный вклад в механику жидкости и газа. В честь Джорджа Стокса названа единица кинематической вязкости стокс,

1 Ст = 1 см²/с = 10⁻⁴ м²/с.

Вы уже знакомы с законом Ньютона для внутреннего трения в жидкости, который связывает между собой напряжение внутреннего трения (напряжение сдвига) и градиент скорости .

(1)

Эта зависимость была получена опытным путём и предложена Исааком Ньютоном в 1687 году для одномерного движения несжимаемой жидкости. Коэффициент пропорциональности , , называют коэффициентом динамической вязкости.

Формула (1) отражает гипотезу И.Ньютона о том, что напряжения сдвига при движении жидкости прямо пропорциональны скорости угловой деформации. Обобщение этой гипотезы на случай трёхмерного пространства осуществил Джордж Стокс. Полученный им закон называют обобщённым законом Ньютона или законом Стокса для внутреннего трения в жидкости.

Связь между напряжённым состоянием жидкости и скоростью её деформации зависит от свойств жидкости и может быть найдена только эмпирическим путём. Закон трения Стокса устанавливает соотношение между напряжённым состоянием жидкости и скоростями деформаций в предположении, что эта связь является аналогичной закону Ньютона.

Это означает, что каждый элемент тензора напряжений может быть выражен через элементы тензора скорости деформаций. Вспомним выражения этих тензоров:

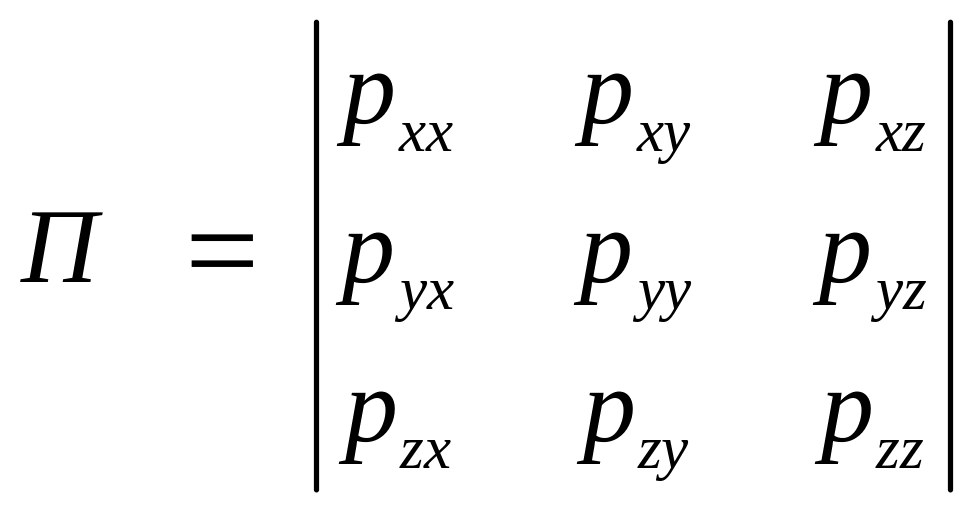
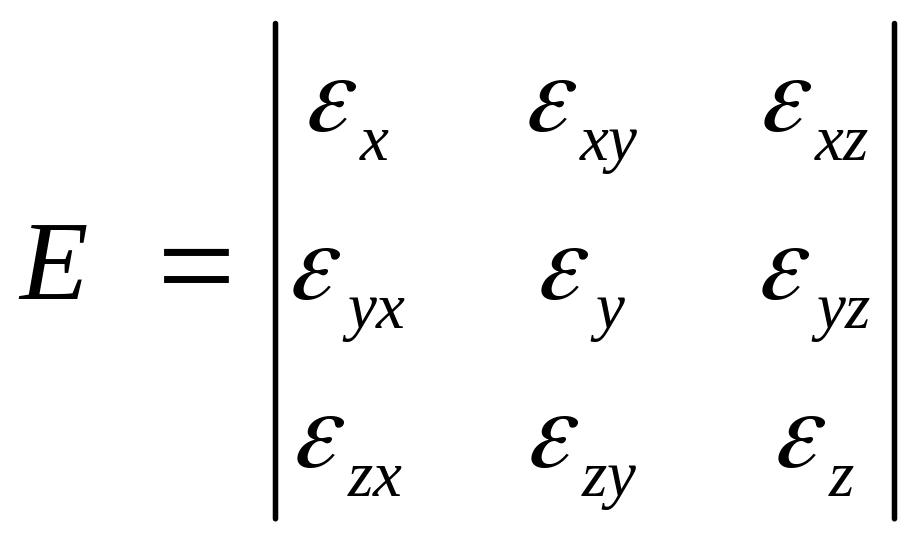(2)

Рассмотренные ранее четыре вида движения жидкости характеризуются следующими величинами:

- поступательное (чисто параллельное) перемещение жидкости определяется составляющими скорости ;

- вращательное (как твёрдое тело) движение определяется составляющими угловой скорости ;

- линейное (или объёмное) расширение (сжатие) определяется скоростью линейной относительной деформации или ;

- искажение геометрической формы определяется скоростями относительной угловой деформации .

Только два последних движения вызывают деформацию элемента жидкости; первые же два движения даже в самом общем случае вызывают только смещение элемента жидкости из его первоначального положения.

Тензор напряжения для покоящейся жидкости имеет вид:

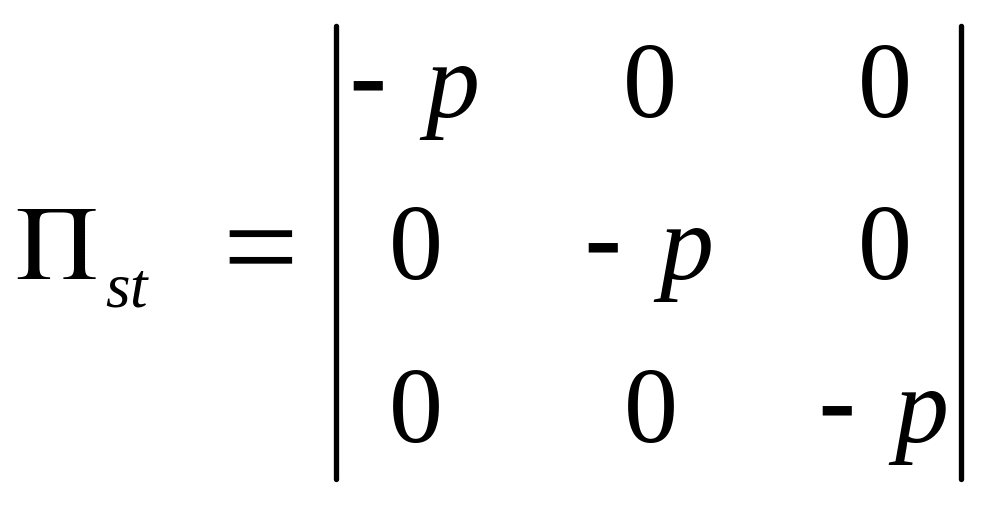(3)

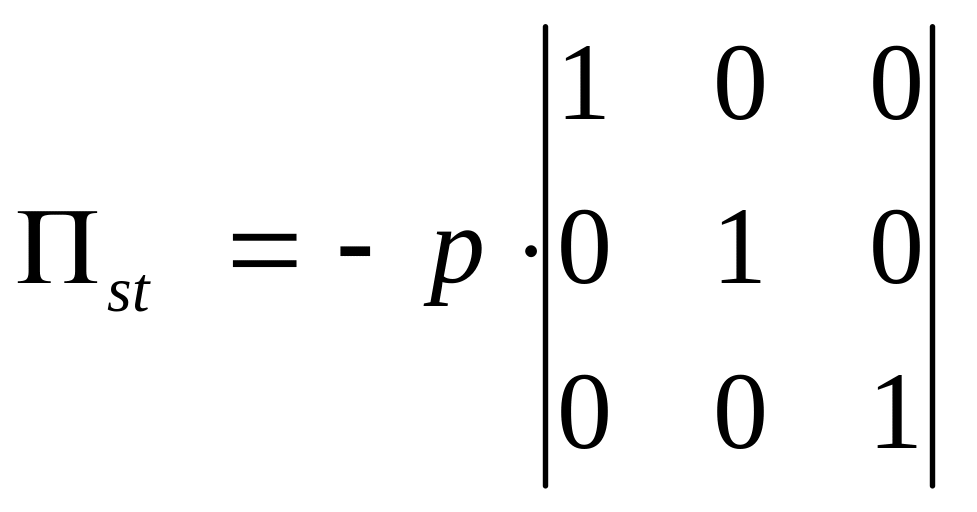или (4)

Девиатор тензора напряжений.

Девиатором тензора напряжений называют тензор, которому соответствует матрица , равная разницы матрицы текущего напряжённого состояния и матрицы статического напряжённого состояния:

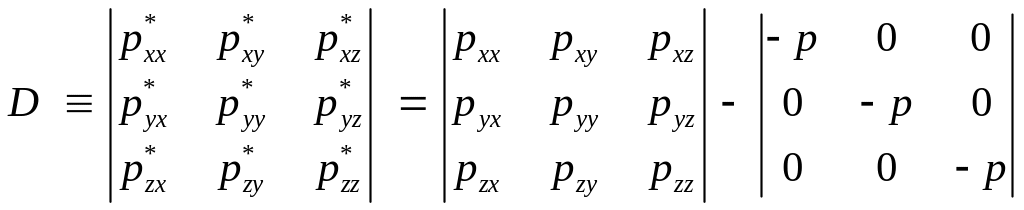(5)

Нормальные напряжения девиатора тензора напряжений и нормальные напряжения тензора напряжений связаны соотношениями:

(6)

Свойства девиатора тензора напряжения:

1. Матрица девиатора тензора напряжения симметрична , поскольку симметричны матрицы, разницей которых она является, см. (5);

2. Девиатор тензора напряжения покоящейся жидкости тождественно равен нулю

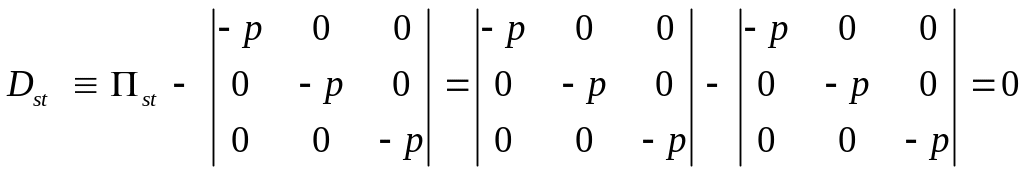(7)

3. В главной системе координат девиатор тензора напряжений имеет диагональный вид, так как матрицы тензора напряжений в главных осях и тензор напряженного состояния покоящейся жидкости имеют диагональный вид;

4. Элементы девиатора тензора напряжений не зависят от величин и . Действительно, эти величины определяют поступательное и вращательное движение жидкости; такое движение представляет собой движение квазитвёрдого тела, которое не сопровождается ни линейными, ни угловыми деформациями.