2.5. Влияние химических соединений

Сопротивление химического соединения выше, чем составляющих его элементов. Это связано с тем, что в результате химического взаимодействия (образование ковалентных или ионных связей) уменьшается число свободных электронов – носителей тока в металле. В результате химического взаимодействия металлическая проводимость вообще может исчезнуть.

Влияние электронных соединений и фаз внедрения на электропроводность иногда схоже с влиянием химического соединения, т.е. приводит к уменьшению проводимости, но возможна и противоположная картина, когда проводимость возрастает.

2.6. Электросопротивление гетерогенных металлических сплавов

Большое влияние оказывает в данном случае размер зерна, а следовательно, дисперсность, а также различия в структурах фаз. Однако если влиянием данных факторов пренебречь, то для отожженного нетекстурированного крупнозернистого сплава с небольшой разницей в проводимости компонентов характерна линейная зависимость электропроводности от объемной концентрации (рис. 4).

Рис. 4. Изменение электропроводности

в сплавах с ограниченной растворимостью

в твердом состоянии

Влияние наклепа и последующего отжига на электросопротивление сплавов, имеющих гетерогенную структуру, определяется не только взаимодействием или устранением искажений пространственной решетки, но и изменением взаимного расположения структурных составляющих. В результате этого наклеп может приводить к уменьшению электросопротивления.

Влияние размера зерна особенно существенно при такой дисперсности зерен, когда размеры зерен одной из фаз (например, включений) соизмеримы с длиной волны электрона (~1 нм). При этом происходит значительное рассеяние электронов, а следовательно, и резкое повышение сопротивления (примерно на 1015 %).

Таким образом, электрические свойства, являясь структурочувствительными, применяются для анализа сплавов в металловедении, например, для определения границ растворимости, изучения превращений в результате термической обработки.

3. СПОСОБЫ ИЗМЕРЕНИЯ ЭЛЕКТРОСОПРОТИВЛЕНИЯ

Двухконтактный. Это самый простой способ. Подсоединение к измерительному прибору (вольтметру) и к источнику тока происходит на одних и тех же контактах образца. В результате вольтметр измеряет сумму падений напряжения: непосредственно на образце и на контактах. Применяется для образцов правильной геометрической формы с электрическим сопротивлением, значительно превышающим контактные сопротивления. В этом случае расчет удельного электросопротивления ведется по формуле:

 = (U / I)^.(S / l). (18)

Трехконтактный. Этот способ применяется, когда доминирует поверхностная проводимость. Исследованию подвергаются дисковые (плоские) образцы. Расчет удельного электросопротивления ведется по формуле:

 = (U / I)(D + h)² / (4), (19)

где  = 3,1415926; D – диаметр плоского внутреннего контакта, м; h – ширина кольцевого зазора между внешним и внутренним контактами, м;  – толщина плоского образца, м.

Четырехконтактный. Места контактов вольтметра и источника тока на образце не совпадают. Вследствие очень большого сопротивления вольтметра через измерительные контакты ток практически не идет, и тем самым вольтметр показывает падение напряжения только на образце (исключается сопротивление контактов). Метод применяется, когда сопротивление образца сравнимо с контактным сопротивлением. В этом случае удельное электросопротивление рассчитывается так:

 = (U / I)^.(S / d), (20)

где d – расстояние между измерительными контактами, м.

Существует также специальный точечный (экспресс-метод) – четырехзондовый метод, когда

 = (U / I)^.2S. (21)

Метод основан на явлении растекания тока в точке контакта металлического острия с проводником. Метод не требует знания величины площади сечения образца и может применяться для измерения удельного сопротивления на образцах любой формы, имеющих одну плоскую поверхность. Четыpехконтактные методы наиболее распространены.

Высокую точность измерения обеспечивает мостовая схема, соединяющая эталонное сопротивление R_x и образец R_s, позволяющая при помощи нуль-гальванометра и манганиновой калиброванной струны добиться равновесия. Для того, чтобы значительно уменьшить влияние контактных сопротивлений, нуль-гальванометр подсоединяется к эталонному сопротивлению и образцу через дополнительные сопротивления R₄ и R₂, величина которых много больше контактных сопротивлений. В результате получается схема двойного моста, рис. 5.

Записывая закон Ома для отдельных участков цепи и учитывая, что через гальванометр при равновесии ток не течет, получаем:

, _R = R₁ / R₃ = R₂ / R₄. (22)

В соответствии с выражением (22) видно, что логично выбрать R₁ = R₂, R₃ = R₄, a R_x  R_s или выше контактного сопротивления.

При достаточных навыках на двойном мосте можно измерить сопротивление 10^–4 –10^–3 Ом с точностью 0,2–0,3%.

У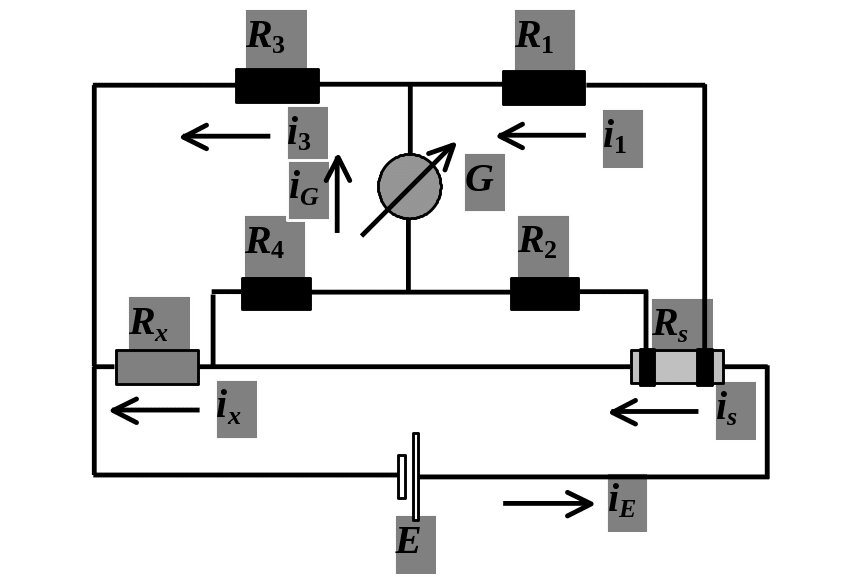 читывая, что при пропускании тока образец нагревается, необходимо вносить поправку на температурную зависимость R_s или держать образец в термостате.

Рис. 5. Схема двойного электрического моста

E – источник питания; G – нуль-гальванометр. Уравновешивание двойного моста происходит подбором сопротивлений на декадных магазинах сопротивлений R₁, R₂, R₃, R₄.