2.1.6. Термоэлектродные материалы

Термопары применяются в качестве измерительных устройств для измерения температуры в широком интервале. Основные требования, предъявляемые к материалам пары термоэлектродных проводов, – это высокие и стабильные значения термо-эдс в диапазоне рабочих температур. Поэтому химический состав таких проводов должен выдерживаться очень точно (прецизионные сплавы).

Как уже было сказано выше, константан применяется в качестве термоэлектродного материала для создания медь-кон­стан­та­но­вых термопар (диапазон рабочих температур: –250300 С) и компенсационных проводов, например, к отрицательным электродам платинородий-платиновых термопар. Из медно-никелевых спла­вов к термоэлектродным относится также копель (МНМц43-0,5); из сплавов на основе никеля  алюмель (НМцАК2-2-1), хромель Т (НХ9,5) и хромель К (НХ9). Хромель Т используется для изготовления хромель-алюмелевых термопар (диапазон рабочих температур –501300 С), а хромель К  для удлиняющих (компенсационных) проводов. Копель используется, например, для изготовления хромель-копелевых (–50800 С), железо-копелевых (0760 С) и медь-копелевых термопар.

Для измерения высоких температур в инертной среде до 3000 С широко используются вольфрам-рениевые термопары (W–26 % Re/W и др.). Для работы в агрессивных средах применя­ются термопары из благородных металлов, например, платиноро­дий-платиновые Pt–10 % Rh/Pt, Pt–13 % Rh/Pt (1001600 С); платинородий-платинородиевая Pt–30 % Rh/Pt–6 % Rh (3001800 С) и другие термопары.

2.2. Основные физические определения и зависимости

Физической константой, характеризующей электрические свойства металла, является его удельное электросопротивление . Величина  определяется природой объекта и не зависит от его формы и размеров. Основой изучения электрических свойств металлов и сплавов является закон Ома, связывающий прямой пропорциональностью разность потенциалов на концах проводника (U) и силу тока (I). Коэффициентом пропорциональности является электрическое сопротивление проводника (R):

U = RI, (1)

которое зависит от размеров проводника:

(2)

где l – длина проводника, а S – площадь его поперечного сечения. В международной системе единиц СИ [R] = Ом; [] = Ом^.м .

Величина обратная :

(3)

называется удельной электропроводностью и измеряется в (Ом^.м)^–1.

Носителями электрического тока в металлах являются электроны, которые до некоторой степени могут быть признаны свободными. В соответствии с определением электрического тока как направленного движения электрически заряженных частиц плотность потока электронов (плотность электрического тока) определяется следующим выражением:

, (4)

где e – заряд электрона; n – концентрация электронов; v_d – дрейфовая скорость электрона. В свою очередь, дрейфовая скорость пропорциональна напряженности электрического поля, где коэффициент пропорциональности  называется подвижностью:

. (5)

А закон Ома может быть записан как

i = E. (6)

Подставляя (5) в (4) и сравнивая с (6), получаем, что электропроводность определяется выражением:

 = en. (7)

В металлах уровень Ферми расположен в разрешенной зоне, и электронный газ сильно вырожден. В этом случае концентрация электронов практически не зависит от темпе­ратуры и температурная зависимость электропроводности опре­деляется температурной зависимостью подвижности.

Электроны в твердом теле движутся не беспрепятственно, они рассеиваются. Рассеивание будет происходить в том случае, если расстояние между рассеивающими центрами по величине соизмеримо с длиной волны электронов. Электроны рассеиваются на тепловых колебаниях и дефектах кристаллической решетки.

Коллективные колебания атомов в кристалле представляют собой звуковые волны, а соответствующие им возбуждения – кванты звука, или фононы. Таким образом, фонон – квазичастица, являющаяся квантом колебаний кристаллической решетки. Температурная зависимость числа фононов определяется выражением:

, (8)

где  – постоянная Планка;  – частота колебаний.

При стремлении температуры к абсолютному нулю в идеальном кристалле число фононов будет стремиться к нулю и удельное электросопротивление также будет стремиться к нулю. Однако реальные кристаллы обладают дефектами строения. Поэтому при низких температурах подвижность определяется рассеянием электронов на дефектах, в основном на точечных (в первую очередь на атомах примеси), так как длина волны электрона в металле ~10^–10 м. Таким образом, вблизи абсолютного нуля будет иметь место некоторое остаточное электросопротивление, определяемое рассеянием электронов на атомах примеси.

Учитывая, что электронный газ в металле сильно вырожден, выражение для подвижности можно записать так:

, (9)

где m_n – эффективная масса электрона; v_F и _F – средняя скорость движения и длина свободного пробега электронов с энергией, близкой к энергии Ферми, соответственно. Средняя длина свободного пробега электрона обратно пропорциональна концентрации фононов. При высоких температурах доминирует рассеяние электронов на фононах, и как следует из (8), . Поэтому имеем:

. (10)

Скорость v_F от температуры практически не зависит. Подставляя (10) в (9), получаем

. (11)

Подставляя (11) в (7), а затем в (3), получаем, что удельное электросопротивление линейно зависит от температуры (рис. 1):

 _T =  ₀[1 +  _T(T – 273)] =  ₂₀[1 +  _T(T – 293)], (12)

где _T – температурный коэффициент электросопротивления.

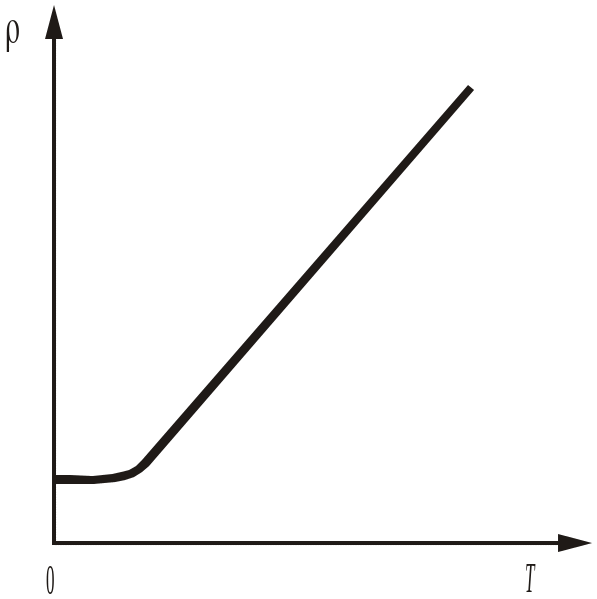
Рис. 1. Зависимость удельного электросопротивления от температуры

Таблица 1

Средние значения удельного электрического сопротивления и температурного коэффициента электросопротивления металлов при 20 С

Металл	106, Омм	T, 1/К
Алюминий Бронза фосфористая Вольфрам Железо Латунь Медь Молибден Никель Олово Свинец Серебро Тантал Хром Цинк	0,028 0,08 0,055 0,098 0,025 – 0,06 0,0175 0,057 0,100 0,115 0,221 0,016 0,155 0,150 0,059	0,0049 0,0040 0,0045 0,0062 0,002 – 0,007 0,0039 0,0033 0,0050 0,0042 0,0041 0,0036 0,0031 0,0030 0,0035

Для всех чистых металлов, за исключением переходных, _T  3,67^.10^–3 1/K . Аномально изменяется при повышении температуры электросопротивление ферромагнетиков, что обусловлено их спонтанной намагниченностью. Выше точки Кюри показатель (T) этих материалов изменяется нормальным образом.

Средние значения ₂₀ и _T для ряда металлов приведены в табл. 1.