Глава 10

Биологический уровень организации материи

1. Структурные уровни организации живой материи

Структурные уровни организации живой материи отражают критерий масштабности мира живой природы. Деление живой материи на уровни весьма условно, но отражает системный под­ход в изучении природы. Вслед за известным генетиком И. В.Ти­мофеевым-Ресовским выделяют четыре уровня организации жи­вой материи: молекулярно-генетический, онтогенетический, по­пуляционно-видовой и биогеоценозный. При этом критериями должны быть элементарные структуры и явления, которые прояв­ляются на данном уровне.

1. Молекулярный, или молекулярно- генетический, уровень — предмет молекулярной биологии и генетики. Рождение этих наук отражает интеграционные процессы в естествознании. В них изучаются механизмы передачи генной информации, про­блемы генной инженерии и биотехнологий. Любая живая систе­ма проявляется на уровне взаимодействия молекул. Знание это­го уровня обеспечивает понимание процессов и на других уров­нях.

Основные структуры — коды наследственной информации — представлены молекулами ДНК. Они разделены по длине на эле­менты кода — триплеты азотистых оснований. Элементарные яв­ления — процессы передачи информации внутриклеточным уп­равляющим системам и связанные с генами мутации. Основные информационные системы используют матричный принцип, т.е. служат матрицами для строительства соответствующих макромо­лекул. Матрицей при синтезе белков в клетках служит заложен­ный в структуре нуклеиновых кислот определенный код.

2. Онтогенетический уровень — следующий уровень орга­низации жизни, на котором изучается организм как целостная сложная саморегулирующая система, способная самостоятельно существовать. Внутри него выделяют организменный и органно­тканевый подуровни, отражающие признаки отдельных особей, их строение, физиологию, поведение, а также строение, функ­ции органов и тканей живой материи. Онтогенез — процесс реализации наследственной информации, закодированной в за­родышевой клетке. Термин ввел Э. Геккель (1866) для рассмот­рения структурной и функциональной организации отдельных организмов.

Особь, индивид — элементарная неделимая единица жизни на Земле. Элементарная структура — клетка — структурная и функциональная единица, а также единица размножения и раз­вития всех организмов. Клеточный, субклеточный подуровни от­ражают процессы специализации клеток и внутриклеточных вне­дрений. Живая клетка — это сложная высокоупорядоченная сис­тема. В клетке непрерывно совершается как синтез крупных мо­лекул из мелких и простых (анаболические реакции, на которые тратится энергия), так и их распад (катаболические реакции). Со­вокупность этих процессов в клетке, происходящих в специали­зированных органоидах, — метаболизм (обмен веществ). Особи, изучаемые на этом уровне, не существуют абсолютно изолированно в природе, они объединены на более высоком уровне организации — на уровне популяции.

3. Популяционно- видовой — следующий уровень организации жизни на Земле — образуется, когда относящиеся к одному виду особи сходны по структуре, имеют одинаковый кариотип (хромо­сомный набор ядра клетки) и единое происхождение, способны к скрещиванию и дают плодовитое потомство. Популяция — эле­ментарная единица в современной теории эволюции. Популя­ция — совокупность особей одного вида, занимающих одну тер­риторию и обменивающихся генетическим материалом. Популя­ция — часть вида, она более однородна по составу, поскольку между ее особями происходит непрерывный обмен генами. Эле­ментарное явление — мутация. На популяцию могут оказывать давление и вызывать ее изменение мутационный процесс, попу­ляционные волны, изоляция и естественный отбор. При наруше­нии изоляции между различными популяциями происходит скре­щивание или обмен генами. Этот уровень важен при определении численности популяций и эволюции живого.

Вид — генетически замкнутая система. Поскольку между вида­ми не может быть скрещивания, то возникшая мутация не выйдет за пределы вида. Организмы, обитающие на изолированных ост­ровах, образуют подвид, иногда подвид образуют группы популя­ций.

4. Биогеоценозный уровень — следующий уровень структуры живой материи. Популяции разных видов, населяющие участок земной поверхности или водоем с определенными природно-кли­матическими условиями (среда обитания, или геоценоз), и свя­занное с ними сообщество растений, животных и микроорганиз­мов образуют неразделимый взаимообусловленный (с динамич­ными обратными связями) комплекс — биоценоз. Это понятие ввел В. Н. Сукачев (1940). Рациональное использование природы невозможно без знания структуры и функционирования биогео­ценозов. Биогеоценоз автономен и саморегулируем, поэтому яв­ляется элементарной единицей этого уровня и служит средой для входящих в него популяций.

Биомы — крупнейшие относительно стабильные во времени и в пространстве наземные сообщества, тесно связанные с опре­деленными природными зонами и поясами: леса, степи, тундры и т.д.

Биосфера — самый высокий подуровень организации жизни на Земле. Эта область активной жизни охватывает нижнюю часть атмосферы, гидросферу и верхнюю часть литосферы. Термин вве­ден в 1875 г. Э. Зюссом. В. И. Вернадский создал учение о биосфе­ре как активной оболочке Земли, в которой совокупная деятель­ность живых организмов, включая человека, является геохими­ческим фактором планетарного масштаба и значения. Он выделял в биосфере живое, косное (солнечная энергия, почва и т.д.) и биокосное (органическое) вещества.

На биосферном уровне изучаются явления планетарного мас­штаба. Поскольку деятельность человека начинает влиять на био­сферу в целом, то одной из главных проблем является проблема сохранения биосферы как основы всего существующего на Земле, в том числе и человека.

2. Генетический код и биосинтез белка

Все живые организмы состоят из клеток, организация и функ­ционирование которых определяются в основном биохимически­ми свойствами нуклеиновых кислот. В ядрах всех клеток орга­низмов и некоторых других органоидов содержится дезоксирибо­нуклеиновая кислота (ДНК) — носитель наследственной инфор­мации на молекулярном уровне. В ядре клетки молекулы ДНК компактно упакованы с белками-гистонами, и эти комплексы на­блюдались в световой микроскоп в виде хромосом. Направлен­ность интерпретации такова: ДНК → РНК → белок; стрелки со­ответствуют транскрипции и трансляции. Это т.н. центральная догма молекулярной биологии.

Молекула ДНК — хранилище генетической информации, РНК — посредник в организации синтеза белков. Белки играют важнейшую роль во всех живых организмах: они участвуют в по­строении клеток и тканей, являются биокатализаторами (фермен­тами), гормонами, дыхательными пигментами (гемоглобин пере­носит кислород из легких к клеткам), защитой (иммуноглобулин) и др. Белки — природные высокомолекулярные органические со­единения, состоящие из 20 аминокислот, соединенных пептид­ными связями в длинные цепи.

Генные механизмы передачи информации осуществляются по- средствам нуклеиновых кислот ДНК и РНК. Как и любые поли­меры, они построены из большого числа небольших органических молекул — мономеров, называемых нуклеотидами. Число и пос­ледовательность расположения мономеров в полимерной цепи име­ет глубокий смысл. У всех видов, обитающих на Земле, нуклеиновые кислоты (НК) построены по единому плану. Основу структуры состав­ляет каркас из фосфатных остатков РО₄. Они были названы кис­лотами, потому что их фосфатные группы освобождают в раство­рах ионы водорода. В состав НК входят также дезоксирибоза (у ДНК) или рибоза (у РНК) и одно из четырех азотистых оснований. В составе ДНК встречаются четыре разных азотистых основания: А — аденин, Т — тимин, Г — гуанин, Ц — цитозин. Аналогичную структуру имеет и молекула РНК, но в ней тимин заме­нен на У — урацил.

Строение нуклеиновых кислот было расшифровано Уотсоном и Криком (1953). Молекула ДНК состоит из двух полинуклеотидных цепей, спирально закрученных одна вокруг другой. Эти цепи не идентичны, но соединены по принципу комплементарности: основанию А в одной цепи соответствует основание Т в другой, а основанию Г — основание Ц. Молекула РНК представлена одной цепью нуклеотидов. Пары азотистых оснований расположены пер­пендикулярно длинной оси. Они как бы «спрятаны» в ДНК и не контактируют с водой в отличие от гидрофильных сахарных и фосфатных остатков.

Размер ДНК обычно характеризуется тысячами пар нуклеоти­дов (т.п.н.). Размеры молекул ДНК устанавливают определением молекулярной массы в дальтонах и длины в количестве пар осно­ваний. Было установлено экспериментально, что 1·10^-12 м длины молекулы ДНК соответствует молекулярной массе в 1 дальтон, равной 1,66 · 10^{- 27} кг. Масса одного нуклеотида около 300 дальтон, длина одного участка ДНК с парой нуклеотидов 3,4· 10^-10 м. Моле­кулярная масса пары (А—Т) составляет 617 дальтон, а (Г —Ц) — 618 дальтон, 1 000 пар азотистых оснований — 6,175 • 10⁵ дальтон, т.е. 1,026 • 10^{- 18} г. В естественных условиях молекула ДНК доста­точно плотно «упакована», а ее форма меняется в зависимости от определенной стадии жизненных процессов. Размеры ДНК зави­сят от типа организма. Физическая длина ДНК вирусов — десят­ки микрометров, бактерий — десятки миллиметров, а содержа­щихся в клетке человека — 2 м. Поскольку организм человека состоит из 10¹³ клеток, протяженность всей ДНК человека порядка 2 • 10¹⁰ км (для сравнения расстояние от Земли до Солнца 1 а.е. = 1,49 · 10⁸ км).

Для состава ДНК характерны закономерности, известные как два правила А. Чаргаффа:

1. Сумма нуклеотидов, содержащих пуриновые (А,Г) азотистые ос­нования, равна сумме нуклеотидов, содержащих пиримидиновые (Т,Ц) азотистые основания: А + Г = Т + Ц.

2. Содержание аденина равно содержанию тимина (А = Т), а гуанина — цитозину (Г = Ц).

Перед каждым делением клетки количество хромосом, т. е. число молекул ДНК, удваивается. Этот первый процесс — реплика­ция — состоит в раскручивании двойной спирали ДНК на от­дельные цепи, каждая из которых используется в дальнейшем как матрица, или шаблон. На них пристраиваются из свободных нук­леотидов ядра клетки новые цепи по принципу комплементар- ности. Именно комплементарность — основа многих явлений биологической специфичности, связанной с «узнаванием» на мо­лекулярном уровне. Даже говорят, что такие структуры подходят друг к другу как «ключ к замку». Это обеспечивает соединение фермента с субстратом, антигена с антителом, ферментативный катализ, передачу генетической информации и др. Последователь­ность нуклеотидов в ДНК кодирует последовательность амино­кислот в белке.

Код триплетный — три рядом стоящих основания в ДНК (кодон) соответствуют одной аминокислоте, три следующие — другой и т.д.

Комплементарность обеспечивает способность организмов к воспроизведению путем реакций матричного синтеза — реак­ции образования полимера, строение которого определяется дру­гими макромолекулами (матрицами). При синтезе белка инфор­мация с фрагмента ДНК копируется матричным путем (считыва­нием и переписыванием) на синтезируемую информационную одноцепочечную нуклеиновую кислоту — РНК (иРНК или мРНК). Копиро­вание происходит по принципу комплементарности, но вместо тимина включается несколько иное основание — урацил (У). Этот процесс — первый этап биосинтеза белка, происходящий в ядре клетки на участке ДНК, называется транскрипцией. Фрагмент ДНК, с которого считывалась информация, — ген. Ген — функ­ционально неделимая единица наследственного материала, исполь­зуемая для кодирования РНК, первичной структуры белка. Поря­док нуклеотидов в гене столь же важен, как порядок букв в слове. Общее количество генов организма увеличивается с ростом слож­ности организма: от сотен у бактерий до десятков тысяч у высших растений и животных. Совокупность всех генов составляет кон­ституцию организма — генотип.

Второй этап биосинтеза белка — трансляция — происходит в цитоплазме на рибосомах, к которым присоединяется мРНК. На этом этапе происходит перевод с «языка нуклеотидов» на «язык аминокислот». Аминокислоты не могут прямо связываться с ко­донами. Они присоединяются к небольшим транспортным РНК (тРНК).

Г. А. Гамов в целях отыскания однозначного соответствия этих «языков» установил, что каждая аминокислота должна кодиро­ваться группой не менее чем из трех нуклеотидов. В самом деле двойных сочетаний из четырех нуклеотидов (4² = 16) недостаточно, так как аминокислот в белках 20, а троек (4³ = 64) хватает с запа­сом, и одна аминокислота может кодироваться несколькими тройками нуклео­тидов. Набор из трех оснований в РНК, соответствующий опреде­ленной аминокислоте, называют кодоном. У каждой тРНК есть триплет нуклеотидов (антикодон), позволяющий ей связываться с комплементарным этому триплету кодоном на мРНК (иРНК). Гипотеза Гамова была подтверждена экспериментально в 1960-е годы.

Последовательность нуклеотидов в молекуле нуклеиновой кис­лоты, отражающая чередование аминокислот в белке, называют генетическим кодом. Генетический код триплетный и вырож­денный. М. У. Ниренбергер и X. Г. Корана путем биохимических исследований сумели расшифровать генетический код. Так, ко­дон АУГ, соответствующий метионину, служит сигналом к началу процесса синтеза, с него начинается любая иРНК, а все последу­ющие триплеты АУГ просто кодируют метионин. Известны всего три кодона — УАА, УАГ, УГА, которые не кодируют аминокисло­ты, а прекращают сборку белковой молекулы.

Важнейший вывод молекулярной генетики — универсальность генетического кода для всех видов живых существ планеты. Конкретные амино­кислоты кодируются одинаковыми триплетами. Это важнейшее свидетельство единства развития жизни на Земле от одного предка.

2. Закономерности передачи информации и наследования признаков

Ген — единица наследственности, фрагмент молекулы ДНК, определяющий развитие того или иного признака (призна­ков). Дискретные наследственные факторы были открыты Г. Мен­делем (1865), а в 1909 г. заново открыты и названы геном В.Йогансеном.

Генетический материал клетки находится в ее ядре и образует во время деления хорошо видимые структуры — хромосомы, яв­ляющиеся материальными носителями наследственности. Все хро­мосомы клеток тела эукариот парны и составляют двойной, или диплоидный, набор хромосом (2п). Следовательно, в этих клетках находится и двойной набор генов. Диплоидный набор хромосом человека — 46.

Гены, лежащие в одном и том же участке (локусе) парных (го­мологичных) хромосом и влияющие на различные проявления одного и того же признака, называют аллельными, или аллелями. Если оба гена в гомологичных хромосомах одинаковы, то такой организм называют гомозиготным. Если эти гены отличаются (на­пример, один определяет белый цвет цветков, а другой — крас­ный), то такие организмы называют гетерозиготными. Проявле­ние признака (белый или красный) в гетерозиготных организмах зависит от того, какой из них окажется доминантным (актив­ным), а какой рецессивным. Доминантные аллели обозначают про­писной буквой, например А (белые цветки), а рецессивные строч­ной — а (красные). Тогда гомозиготные организмы можно обо­значить как — АА и аа, а гетерозиготные — Аа.

Зрелые половые клетки (гаметы) содержат лишь один, гапло­идный, набор хромосом (1п), т.е. один набор генов. Геном — это совокупность генов в гаплоидном наборе хромосом организма. Для гомозигот АА гаметы будут содержать только аллель А, а для гомозигот аа — только а. Гетерозиготные организмы Аа дают га­меты как с а аллелем, так и с А. При слиянии материнских и отцовских гамет образуется зигота с двойным набором генов и проявление признака зависит от того, какие аллели образовали зиготу. В нашем примере при наборе генов АА и Аа цветки будут белые, а при наборе аа — красные.

Все гены определенного локуса в какой-либо популяции мож­но рассматривать как генофонд (по данному локусу). Для харак­теристики состава популяции по этому гену вводится понятие ча­стоты (доли) гена или, точнее, аллеля. Пусть А — доминантный аллель; а — рецессивный аллель; N— число особей в популяции; D — число гомозиготных особей с генотипом АА; Н — число гете­розиготных особей с генотипом Аа; R — число гомозиготных осо­бей с генотипом аа. Общее число генов равно 2N, так как каждая особь содержит 2 аллеля.

Частоту генов А в популяции вычисляют по формуле

Частота генов а равна:

На частоты генов влияют мутационное давление и отбор. Ко­лебания численности популяции под действием различных фак­торов также может вызвать изменение генетической структуры.

Знание частот р и q позволяет рассчитать частоты распределения гомозигот и гетерозигот в свободно скрещивающейся популяции при отсутствии отбора, мутирования по этому гену и миграции. Эти частоты распределения устанавливаются в соответствии с за­коном Харди — Вейнберга:

p² + 2pq + q² = 1,

где р² — доля гомозигот АА; 2pq — доля гетерозигот Аа; q² — доля гомозигот аа.

При рецессивных мутациях, снижающих жизнеспособность осо­бей, подвергаются отбору только гомозиготы по мутантному гену. Поскольку гетерозиготные особи остаются, то мутантные гены в популяции сохраняются. Количество дефектных генов, присут­ствующих в каждый данный момент в популяции, называют ге­нетическим грузом. Используя закон Харди —Вейнберга, мож­но рассчитать динамику изменения частоты генов в популяции. Коэффициент отбора S определяет долю погибающих гомози­гот: S =1, если гомозиготы полностью нежизнеспособны, в ос­тальных случаях S < 1. При S = 1 частоту генов в популяции вы­числяют по формуле

,

где п — число поколений. При S < 1 для каждого следующего поколения q определяется так:

Закон Харди — Вейнберга (1908) показывает, что само наследо­вание не меняет частоты аллеля в популяции. Это означает, что при свободном скрещивании генетическая структура сохраняет­ся, не изменяется, что выражается коэффициентами частот раз­ложения бинома.

Лекция 11

Неравновесная термодинамика открытых систем

1. Динамические и статистические закономерности

Идеалы классической науки определялись чисто детерминис­тическим стилем мышления — простота, линейность, исключе­ние неопределенности и случайности. В связи с этим было стрем­ление найти однозначные динамические законы, которым бы под­чинялись все явления действительности, и потому случайность и время были исключены из сложившейся картины мира. Развитие понималось как поступательное, без альтернатив; все случайное изгонялось из теорий, а неравновесность и неустойчивость рас­сматривались как досадные неприятности. Мир был жестко свя­зан линейными причинно-следственными связями, причем след­ствие было всегда пропорционально причине.

Динамическая система — это модель реальной физической, химической, биологической, социальной или какой-либо другой системы. Для определения динамической системы нужно задать параметры, определяющие ее состояние, и указать правила (опе­ратор эволюции), по которым можно определить ее состояние в последующий момент времени.

Динамические системы отражают принцип детерминизма. Про­стота законов, по которым движутся небесные тела, и соотноше­ния между их массами и расстояниями позволяют проанализиро­вать их движения до определенной точки. Чтобы предсказать по­ложение тел в будущих веках, математику достаточно знать их положение и скорость из наблюдений в один момент времени. Однако незнание различных причин, вызывающих какие-либо со­бытия, а также их сложность в сочетании с несовершенством тех­ники и анализа мешают достигнуть той же точности предсказа­ний в огромном числе явлений. Поэтому П. С. Лаплас, один из создателей теории вероятностей, считал случайность в законах природы следствием несовершенства наблюдений.

Появление статистических теорий (теория азартных игр, те­ория ошибок измерений, статистическая механика и физика, де­мографические исследования, статистика преступлений и др.) из­меняло стиль мышления на вероятностный. Казалось бы, инди­видуальные результаты опытов ведут себя «непредсказуемо», но последовательность большого числа одинаковых экспериментов обнаруживает устойчивость. Большие макросистемы можно опи­сывать динамическими уравнениями, но решение задачи стано­вится нереальным. Это понял Дж. Максвелл, и была построена статистическая механика. Статистическая теория позволяет пред­сказывать лишь вероятности тех или иных значений величин, ха­рактеризующих систему. Здесь появлялся хаос, хаос микроскопи­ческий. С тем же типом хаоса, что и при тепловом движении частиц газа, мы сталкиваемся, рассматривая испускание света лам­пами, световое поле которых состоит из отдельных световых волн, испускаемых атомами совершенно независимо и беспорядочно.

В отличие от динамических теорий статистические теории учи­тывают флуктуации величин и даже придают им большое значе­ние. Постепенно складывалось понимание, что статистические теории более фундаментальны, чем динамические. Они описыва­ют более широкий класс явлений, дают более полное описание, чем их динамический аналог.

Более серьезный удар по лапласовскому детерминизму нанес В. Гейзенберг своим принципом неопределенностей. На основе этого принципа нельзя, например, предсказать процессы, проис­ходящие в атомном ядре (радиоактивный распад), сколько бы све­дений о процессах мы не получали. Но соотношения неопреде­ленностей показывают, что может реализоваться некоторая ко­нечная область значений параметров. И на небольших временных интервалах неопределенность состояний невелика и нарастает достаточно медленно. Создание квантовой механики завершило переход к новой картине мира, где вероятность и случайность стали веду­щими.

Но вне микромира для небольшого числа частиц ситуация ока­залась сложнее. Например, движение маятника можно описать двумя переменными (скоростью и отклонением от равновесия), поведение маятника предсказуемо, соответствует детерминизму. Но при добавлении еще одной переменной, например, связав маятник пружинкой с моторчиком и возмущая его колебания вынуждающей силой, можно получить беспорядочное движение. Это будет хаос совершенно другого типа — динамический хаос, так как движение маятника описывается динамическими уравне­ниями.

На динамический хаос указал еще в начале XX в. А. Пуанкаре. Он предположил, что вблизи каждого тела есть малозаметные факторы, вызывающие нерегулярности. И поведение даже про­стой системы начинает так сильно зависеть от малых изменений начальных условий, что делается непредсказуемым. В 1960-е гг. была обнаружена возможность случайных явлений, от которых нельзя избавиться уточнением начальных условий и подробней­шим описанием воздействий на выделенную систему даже в са­мых простых системах. Такие движения возникают в механиче­ских и электрических нелинейных колебательных системах. Если возмущения системы затухают со временем, стремясь к нулю, ре­жим функционирования динамической системы устойчив и пред­сказуем. Если же малые возмущения нарастают, возникает неус­тойчивый режим.

Так, метеоролог Э. Лоренц открыл хаотическое движение, об­наружив его при решении на компьютере простой системы гид­родинамических уравнений. Он для возможности предсказания погоды рассматривал термоконвекцию в подогреваемом снизу слое жидкости в поле силы тяжести. Сильно упрощая уравнения, Ло­ренц решал систему всего трех уравнений. Он обнаружил в фазо­вом пространстве трех измерений область, которая как бы притя­гивала к себе траектории из окрестных областей. Эту область на­звали аттрактором (от англ. — притягивать). В этой области траектории сразу запутывались, поведение системы становилось полностью непредсказуемым. В ней система была очень чувстви­тельна к малейшему изменению начальных условий, эта чувстви­тельность даже получила красочное название «эффект бабочки». Такая чувствительность противоречит интуитивным представле­ниям о механическом движении. Оказалось, что к модели Лорен­ца сводятся многие системы. Резкое изменение будущего в зави­симости от малейшего изменения начальных условий можно пред­ставить, если, например, металлический шарик ронять на острие бритвы.

Существование динамического хаоса гарантирует быстрое пре­вышение пределов предсказуемости, не оставляя надежд на дол­госрочные прогнозы. В дополнение к принципу неопределенности Гейзенберга неустойчивость траекторий, характерная для хаотичес­кой динамики, нанесла еще один удар по детерминизму Лапласа.

Важной особенностью хаотического движения является нали­чие в уравнениях Лоренца нелинейных членов. Система диффе­ренциальных уравнений имеет простой вид (нелинейность из-за произведения zx):

ẋ = - y - z, ẏ = х - ay, ż = b + z(x - y).

С нелинейностями встречаются часто. Так, искажение сигнала при прохождении через среду обусловлено нелинейными эффек­тами. При прохождении через линейную среду он может осла­беть, но не изменится. В социальных и экономических системах нелинейность тоже проявляется в виде взаимодействия. Но в этих науках она чаще всего связана с психологией индивидуума или группы лиц. И ввиду сложности описания явления в них рассмат­ривали как линейные. Так, считали, что инвестор всегда реагиру­ет линейно на полученную информацию, или реагирует на нее сразу после получения, не ожидая ее накопления или последую­щих событий. Это означает, что прошлая информация всегда сра­зу учтена и отражена в стоимости бумаг на данный момент. Цены отражают всю имеющуюся информацию, и изменения в цене не соотносятся между собой. Можно показать, что в рамках линей­ной модели прибыли нормально распределены и практически независимы. Нелинейные эффекты возникают прежде всего в пси­хологии человека. Люди не сразу реагируют на изменения, неко­торые любят риск, много предубеждений в оценках и пр.

С уче­том этого получим нелинейную модель.

Если система в начальный момент времени находилась в неко­торой области фазового пространства, то со временем она может попасть в область аттрактора и не будет ее покидать. Если выб­рать две близкие точки и проследить за ними, то можно заметить, что со временем τ они расходятся. Расстояние между ними растет по экспоненте, т.е. пропорционально e^λτ . Входящая в показатель экспоненты постоянная λ называется показателем Ляпунова. Если λ > 0, мы имеем дело с хаотическим аттрактором, поскольку пока­затель отражает чувствительность от начальных условий. Траек­тории с течением времени заполняют область аттрактора. Но, как оказалось, не целиком, и это связано с явлением самоподобия хаотических траекторий. Как бы мы не увеличивали фигуру, она оказывается той же формы. Так возникло понятие фрактала и фрактальной размерности.

Под фракталами понимают множества, демонстрирующие на разных масштабах разрешения своей геометрической структуры свойства подобия в строгом или приближенном смысле. К фрак­талам относятся и объекты природы, обладающие этим свойством. Есть такое определение: «Фракталом называется структура, со­стоящая из частей, которые в каком-то смысле подобны целому» (Б. Мандельброт). На практике встреча с фракталами произошла, когда Л. Ричардсон попытался измерить длину береговой линии Британии. Ему пришлось заменять реальную извилистую линию ломаной линией, состоящей из множества отрезков.

Складывающийся сейчас системный стиль мышления не отме­няет вероятностного видения мира, но дополняет его такими важ­нейшими элементами, как сложность, системность, целенаправ­ленность.

Сложные системы в отличие от простых, описываемых не­сколькими параметрами, состоят из большого числа переменных и большого числа связей между ними. В сложной системе появля­ется из-за внутренних взаимодействий много свойств, которых нет у ее частей (эмерджентные свойства), они — следствие цело­стности системы.

Открытые системы — это системы, которые обмениваются с окружающей их средой веществом, энергией или информацией. В каком-то смысле все существующие системы и есть открытые.

Поведение открытых систем учитывает не только законы, уста­новленные для закрытых систем, но и подчиняется своим особым законам, связанным взаимодействием с окружением. С молеку- лярно-кинетической точки зрения, в изолированных системах положение равновесия отвечает максимальному значению энтро­пии S_max системы (состояние максимального хаоса). Исследова­ние открытых систем возможно на основе только термодинамики необратимых процессов: в них энтропия может возникать и пере­носиться.

2. Открытые системы, находящиеся вблизи термодинамического равновесия

На пути любой достаточно сложной системы к равновесию, которое характеризуется S_max , встречаются препятствия. Таковы­ми выступают граничные условия. Если они постоянны, напри­мер, поддерживают градиент температуры ΔT на границах, то пе­ременные состояния стремятся асимптотически к независящим от времени величинам, достигая квазистационарного или ста­ционарного состояния. Стационарные состояния в открытых си­стемах биолог-теоретик Л. Берталанфи назвал текущим равнове­сием. Он построил теорию биологических организмов на базе обобщений физической химии, кинетики и термодинамики, на­звав ее теорией открытых систем. Берталанфи ввел формаль­ное выражение таких важных свойств системных параметров, как сумма, целостность, организация, рост, конкуренция и т.д., широко применяя аппарат дифференциальных уравнений. Поня­тие локального, или текущего, равновесия он ввел для живого организма — неравновесной открытой системы. Такие, близкие к равновесным, состояния систем встречаются в различных облас­тях естествознания.

Понятие локального равновесия вводят при медленном изме­нении внешнего воздействия и для времен, больших характерно­го времени элементарного релаксационного процесса, формиру­ющего равновесие. Принцип локального равновесия ограничива­ет число систем, доступных термодинамическому рассмотрению. В гигантской фабрике естественных процессов принцип энтро­пии занимает место директора, который предписывает вид и по­рядок исполнения всех сделок. Закон сохранения энергии играет роль бухгалтера, который приводит в равновесие дебет и кредит. Для биологических систем, принципиально открытых, такой подход оказался очень плодотворным.

В неравновесной системе все ее характеристики, в том числе и энтропия, зависят от времени. Так, при контакте двух подсистем, имеющих разную температуру, суммарная энтропия системы, со­гласно второму началу термодинамики, будет увеличиваться, если в целом система является замкнутой. Вследствие теплообмена система будет производить энтропию и dS/dt > 0, пока система не достигнет равновесия.

Внутреннее производство энтропии за единицу времени в еди­нице объема σ = dS/dt названо И. Р. Пригожиным функцией дис­сипации. Изменение энтропии открытой системы будет зависеть от ее производства внутри самой системы и оттока или притока энтропии в результате обмена с окружающей средой. Если гранич­ные условия постоянны (и при небольших значениях градиентов и интенсивности потоков), например, поддерживают определенную разность температур на границах, то переменные параметры состо­яния системы через некоторое время перестанут зависеть от време­ни. Система будет в неравновесном стационарном состоянии, близ­ком к равновесному, т.е. в состоянии текущего равновесия.

Если для изолированной системы термодинамическим потен­циалом является энтропия, для замкнутой системы с заданной температурой — свободная энергия, то для слабо неравновес­ных систем таким потенциалом является производство энтро­пии. В линейной области система стремится к стационарному со­стоянию, в котором минимально производство энтропии.

Поскольку это состояние стационарно, все его характеризую­щие величины перестают зависеть от времени, среди них и энтро­пия. Тогда ΔS = 0, но оно состоит из суммы двух членов — потока энтропии ΔS_e и ее положительного производства ΔS_и. Поэтому ΔS_e = - ΔS_и < 0. Отрицательный поток энтропии означает, что си­стема поставляет энтропию окружающей среде и увеличивает хаос вокруг за счет активности внутри. Поступающий из внешней сре­ды поток тепла или вещества определяет отрицательный поток энтропии ΔS_e , который компенсируется производством энтропии ΔS_и за счет необратимых процессов внутри системы. Теорема о минимуме производства энтропии выделяет то стационарное со­стояние, к которому система стремится, где перенос энтропии в окружающую среду настолько мал, насколько позволяют это гра­ничные условия. Можно сказать, что эта теорема выражает свое­образную «инерцию» системы — стремится к состоянию, макси­мально приближенному к равновесию.

В соответствии с теоремой Пригожина такому стационарному состоянию соответствует минимальное производство энтропии. Если граничные условия не позволяют системе прийти в устойчи­вое равновесие, где внутреннее производство энтропии равно нулю, она придет в состояние с минимальным производством энтро­пии. Системы, в которых функция диссипации σ = dS/dt ≠ 0, он назвал диссипативными. Поскольку «диссипация» происходит от лат. dissipatio — разгонять, рассеивать, то говорят, что эти струк­туры летучие и возникают при рассеянии свободной энергии. Ме­няя потоки энергии и вещества, в открытых системах можно ре­гулировать образование диссипативных структур. Энергия упоря­доченного движения переходит в энергию неупорядоченного дви­жения и, в конечном счете, в тепло. Практически все системы яв­ляются такими, так как трение и прочие силы сопротивления приводят к диссипации энергии.

Устойчивость стационарных состояний системы с минималь­ным производством энтропии связана с принципом, сформули­рованным в 1884 г. в химии Ле Шателье и обобщенным в 1887 г. с точки зрения термодинамики К. Брауном.

Принцип Jle Шателье — Брауна в современном изложении оз­начает, что система, выведенная внешним воздействием из состо­яния с минимальным производством энтропии, стимулирует раз­витие процессов, направленных на ослабление внешнего воздей­ствия. Аналогичный принцип в электромагнитных явлениях от­крыт Э.Х. Ленцем (правило Ленца, см. гл. 7).

Принцип локального равновесия и теорема о минимуме про­изводства энтропии в равновесных состояниях были положены в основу термодинамики необратимых процессов, а их автор И. Р. Пригожин стал лауреатом Нобелевской премии по химии за 1977 г. Основное достижение термодинамики неравновесных про­цессов состоит в признании того факта, что общим свойством открытых систем является их самоорганизация. Именно самоор­ганизация в открытых системах выступает в качестве противодей­ствия росту энтропии.

3. Энтропийный баланс живых организмов и Земли

Наша Земля не является замкнутой системой, она движется в космическом пространстве, и взаимодействие с этой окружающей средой позволяет ей поддерживать отрицательный энтропийный баланс, создавая условия для эволюции в геосфере. Сам процесс получения энергии от Солнца ничего не меняет, поскольку на Земле почти вся энергия переизлучается обратно в космос, как и в каж­дом живом организме в окружающую среду. Э. Шредингер в сво­ей книге «Что такое жизнь с точки зрения физики?» подчеркива­ет, что неравновесное состояние живых систем поддерживается за счет окружающей среды, назначение обмена веществ — пониже­ние энтропии. Существует два механизма понижения энтропии.

1. Создание высшего порядка из порядка низшего уровня. Для растений, к примеру, мощным фактором понижения энтропии является солнечный свет, с использованием которого в хлорофилле происходит фотосинтез — повышение упорядоченности дегради­рованных веществ. Механизм поддержания упорядоченности в живых организмах сейчас детально исследуется. Возможно, скоро для оценки качества пищи будут использовать не только ее вкус и калорийность, а также способность понижать энтропию.

2. Создание порядка из хаоса (самоорганизация). Изучением этих процессов в системах любой природы занимается синерге­тика. Об этом пойдет речь в подразд. 11.4. Синергетика занима­ется открытыми сильно неравновесными процессами в таких си­стемах, как атмосфера Земли, процессы горения, турбулентности, явления в плазме, процессы в обществе, демография и пр.

Энтропия производится при любых процессах в геосфере, и пусть это производство составляет ΔS₃ dS = dQ/T. Земля получает от Солнца вместе с теплом Q ≈ 10²⁵ Дж (при температуре Т₁ = 6 000 К) тоже некоторое количество энтропии: ΔS_ВХ = Q/T₁. Но Земля долж­на избавляться от излишка тепла (иначе нагревалась бы), и она тоже, как нагретое тело, испускает тепловое излучение при Т₂ ≈ 300К. При этом Земля выбрасывает в космос такое же количество энер­гии, что получает от Солнца, только более низкого качества, со­ответствующего более низкой температуре. В космос уходит и поток энтропии ΔS_ВЬ1Х = Q/T₂. Видно, что поток уходящей энтропии пре­восходит входящий в Т₁/Т₂ = 20, т.е. в 20 раз.

Выброс такого количества энтропии компенсирует и входящий поток, и внутреннее производство энтропии: ΔS_BX + ΔS₃ < ΔS_ВЫХ. Это неравенство и отражает отрицательный энтропийный баланс Земли. Шредингер назвал подобную ситуацию «добываем негэнтропии из окружающей среды». Благодаря этому возможны раз­нообразные процессы в геосфере, и пока он отрицателен, сохра­няется возможность устойчивого развития земных систем — гео­физических, биологических, социальных. Каковы перспективы со­хранения этого неравенства?

Из астрофизики известно, что входящий поток энтропии мож­но считать постоянным почти на протяжении 3 — 5 млрд. лет. Поток, выбрасы­ваемый в космос, тоже вряд ли изменяется, поскольку определяет­ся средней температурой на Земле, которая колебалась на 2 —3 %. Более динамично меняется производство энтропии в геосфере. Чем интенсивнее идут процессы на Земле, тем больше ΔS₃. С по­явлением человека, а тем более с возникновением цивилизации, скорость производства энтропии резко растет. Например, до ци­вилизации прошлого века ядро урана-235 делилось в среднем за 1 млрд. лет, а человек ускорил этот процесс — в ядерном реакто­ре деление происходит за месяц, а в бомбе — за доли секунды! Так же ускорилось производство энтропии.

Совокупность дел человека привела энтропийный баланс к опасной черте, и нужно искать пути более эффективного произ­водства и мудрых политических решений управляемого развития.

4. Открытые системы, находящиеся вдали от состояния термодинамического равновесия

При существенных потоках вещества и энергии, которыми об­менивается открытая система с окружающей средой, к ней уже не применимы представления равновесной термодинамики. Вдали от равновесия стационарное состояние различно реагирует на раз­ные типы флуктуаций. В ряде случаев флуктуации не затухают, а усиливаются системой, вынуждая ее эволюционировать к новому режиму, который может отличаться качественно от тех стацио­нарных состояний, которые соответствовали минимуму производ­ства энтропии. Такие системы называют сильно неравновесны­ми. При такого рода неустойчивости нужно указывать порог, за которым появляется новый режим, отличный от равновесного или слабо неравновесного. Данные явления известны в различных си­стемах живой и неживой природы: в гидродинамике (переход ла­минарного течения в турбулентное), в химии (реакции Белоусо­ва—Жаботинского), в теплопередаче (неустойчивость Бенара), в оптике (переход лазера в режим генерации) и др.

В таких системах суммарное уменьшение энтропии за счет об­мена потоками с внешней средой при определенных условиях может превысить ее внутреннее производство. Появляется неус­тойчивость однородного неупорядоченного состояния, возника­ют флуктуации, и они могут возрасти до макроскопического уров­ня. Флуктуациями называют случайные отклонения какого-либо параметра системы от его средних значений. При этом из хаоса могут возникнуть структуры, которые начнут последовательно переходить во все более упорядоченные. Образование этих струк­тур происходит не из-за внешнего воздействия, а за счет внутрен­ней перестройки системы, поэтому такое образование структур получило название самоорганизация. Для описания процессов са­моорганизации уже нельзя пользоваться представлениями линей­ной термодинамики необратимых процессов.

Процессы самоорганизации описываются нелинейными урав­нениями для макроскопических функций. Этим занимается си­нергетика — новое научное направление, в котором изучаются процессы перехода от хаоса к порядку и обратно в открытых не­линейных системах, далеких от равновесия. Оказалось, что под действием крупномасштабных флуктуаций возникают коллектив­ные формы движения, называемые модами, между которыми воз­никает конкуренция, происходит отбор наиболее устойчивых из них, что и приводит к спонтанному возникновению макроскопи­ческих структур.

Классическим примером возникновения упорядоченной струк­туры является конвективная ячейка Бенара (рис. 11.1).

Наблюдалось появление упорядоченных структур в ртути, на­литой в широкий плоский сосуд, подогреваемый снизу. Слой рту­ти (или другой вязкой жидкости) после того, как градиент темпе­ратуры достиг некоего критического значения, распадался на оди­наковые шестигранные призмы с определенным соотношением между стороной и высотой. В центральной части такой призмы жидкость поднималась вверх, а по граням — опускалась. По по­верхности жидкость растекалась от центра к краям, а в придон­ном слое — к центру. Начиная с критического значения разницы температур возникли устойчивые структуры, названные ячейка­ми Бенара.

В сильно неравновесных системах понятие вероятности, лежа­щее в основе принципа Больцмана, становится неприменимым. Так, в этих случаях нет хаоса и большого разброса скоростей, на­оборот, когерентное движение означает, что многие молекулы начинают двигаться почти с одинаковыми скоростями! Если опи­раться на принцип Больцмана, то флуктуация, макроскопическое конвективное движение, должна исчезать, но она усиливается и завладевает всей системой. Тенденция выравнивания и «забыва­ния» начальных условий перестает быть общей тенденцией!

Существование равновесной структуры (например, кристалла) объясняется по классической термодинамике из принципа Боль­цмана. Ячейки Бенара — той же структуры, но иной природы,

Рис. 11.1. Структура ячеек Бенара (вид сверху)

такая структура отвечает некоторой форме супермолекулярной организации. Если параметры, описывающие кристаллические структуры, могут быть выведены из свойств образующих их моле­кул (из радиуса действия сил взаимного притяжения и отталкива­ния), диссипативные структуры отражают ситуацию в порождаю­щей их неравновесной системе. Описывающие их параметры мак­роскопические — в несколько сантиметров, а не 10^{- 8} (характер­ный масштаб межмолекулярных сил). Временные масштабы тоже макроскопические — секунды, минуты, часы, а не 10^{- 15}, как пе­риоды колебаний отдельных молекул. Каждая ячейка содержит около 10²¹ молекул, значит, такое огромное число молекул мо­жет демонстрировать согласованное (когерентное) поведение, не­смотря на случайное, хаотическое поведение каждой молекулы. В ячейке Бенара тепловой поток становится параметром по­рядка.

Кроме того, несмотря на идеальную воспроизводимость дан­ного эксперимента, вещество структурируется в ячейки Бенара с попеременно право- и левовращательным движением. Этот факт предсказуем, т.е. детерминирован. Но предсказать направление вращения в каждой ячейке невозможно, тут играет роль случай. Итак, вдали от равновесия при одних и тех же параметрах макро­скопической системы возможно несколько различных решений. Этот дуализм отличен от корпускулярно-волнового дуализма, про­являющегося в микромире. Здесь эффект, определяемый случаем, макроскопический. Возникающие структуры более высокоорга­низованны, т.е. энтропия понижается.

За порогом неустойчивости возникают новые явления. В каж­дой из систем находятся свои управляющие параметры, которые выводят систему за пороговое значение. Для химических реакций в таковой роли выступает концентрация веществ, в ячейке Бенара — градиент температуры, в гидродинамике — скорость потока и т.д. Система может самопроизвольно покинуть стационарное состоя­ние под действием флуктуаций. Судьба флуктуаций, возмущаю­щих химическую систему, а также новые ситуации, к которым система может прийти, зависят от детального механизма реакций. При любых начальных условиях она стремится выйти на предель­ный цикл, периодическое движение по которому устойчиво. Кри­тический порог становится как бы неустойчивым фокусом, вый­дя за который, система ведет себя странно. Обычно это критиче­ское значение параметра соответствует точке бифуркации. Вмес­то того чтобы оставаться стационарными, концентрации, к при­меру в химической реакции, начинают колебаться с явно выра­женной периодичностью. Такой периодический процесс был на­зван химическими часами.

В сильно неравновесной области нет универсального закона, который мог бы описать поведение всех систем. В каждой систе­ме есть свои отличия. В последовательности химических реак­ций, например, устойчивости стационарного состояния могут уг­рожать только стадии, содержащие автокаталитические петли (т.е. стадии, в которых продукт реакции участвует в синтезе само­го себя). Этот вывод подводит к фундаментальным достижениям молекулярной биологии. В теории такие процессы описываются нелинейными уравнениями.

В ячейках Бенара, возникающих вдали от равновесия, при даль­нейшем удалении от него конвективный поток начинает коле­баться вплоть до возникновения турбулентности. Взаимодействие колебаний с разными частотами способствует возникновению боль­ших флуктуаций, и тогда говорят о возникновении хаоса. Про­странственные и временные параметры имеют в этом случае мак­роскопический масштаб. Часто порядок и хаос меняются места­ми, и эволюция системы через последовательность бифуркаций становится необратимой, т.е. детерминированность частот порож­дает случайность, обусловленную огромным числом частот, уча­ствующих в процессе. Путь к хаосу определяется открытыми Фейгенбаумом законами — последовательностью бифуркаций удво­ения периода.

Ячейки Бенара являются упрощенной моделью самоорганизу­ющейся биосферы, воспроизводя условия жизни на Земле. Зна­ние пределов применимости принципа Больцмана и новое пони­мание энтропии, хода времени и эволюции открывает перспекти­вы прогнозирования в системах самой разной природы, в том числе и социальных.

Синергетика — это теория самоорганизации в системах раз­личной природы. Она имеет дело с явлениями и процессами, в результате которых у системы могут появиться новые свойства, которыми не обладает ни одна из ее частей. Вслед за создателем синергетики Г.Хакеном (1973) выделим кратко ее основные чер­ты.

Характерные черты синергетики:

1. открытость рассматриваемых систем (внешние силы могут задаваться с помощью уравнений движения, т. е. неявно, и соот­ветствующие им силы называют параметрами порядка, которым подчинены остальные переменные — отсюда возможность);

2. нелинейность сред, в которых эти системы существуют;

3. саморганизация и самодостраивание структур;

4. эволюционирование систем и неоднозначность путей эво­люции, выбираемых через точки бифуркации;

5. порядок через флуктуации;

6. наличие катастрофических изменений при малых случай­ных воздействиях («эффект бабочки»).

Открытость, нелинейность и хаос — лишь предпосылки са­моорганизации.

Флуктуации и бифуркации — промежуточные характеристи­ки процесса.

Параметры порядка — это то, что ведет систему по пути мак­росостояний, аттракторы — это то, куда система идет.

Лекция 13

Концепции эволюции в мегамире

1. Структура и строение мегамира

Метагалактика — доступная наблюдениям часть Вселенной, воспринимаемая как единое целое. Поскольку возраст Вселенной составляет 13—15 млрд лет от начала расширения, наибольшее расстояние составляет 13— 15 млрд св. лет. Его называют кос­мологическим горизонтом. Из-за космологического горизонта свет до нас не успеет дойти, горизонт расширяется со скоростью света 300 000 км/с, т. е. размеры Метагалактики все время растут. В Ме­тагалактику входит все, что может зафиксировать телескоп, — миллиарды галактик, квазаров, электромагнитные излучения, при­чем вещество распределено неравномерно.

Наблюдения и подсчеты числа галактик показывают, что Ме­тагалактика имеет явно ячеистую структуру — вдоль границ яче­ек расположены галактики, а внутри их — огромные пустоты (войды). В местах пересечения границ ячеек (в узлах) может быть до 10 тыс. галактик, такие группы называют сверхскопления. Сверхскопления складываются в нити и ленты, придавая Все­ленной в самом грандиозном масштабе губчатую структуру. Если рассматривать распределение вещества в масштабах больших размеров ячеек (более 200 Мпк), то оно окажется удивительно равномерным и однородным, тогда как при меньших масшта­бах — сильно неоднородным. Исследования по определению его плотности ведутся интенсивно, но пока вопрос остается откры­тым. Оценки средней плотности вещества во Вселенной (3 • 10^{- 27}— 10^{- 26}) кг/м³.

Скопления галактик состоят из сотен или тысяч галактик, имеют почти шаровую форму размером 1 — 3 Мпк. Так, в бли­жайшее к нам скопление (расположенное на расстоянии около 20 Мпк, находящееся в созвездии Девы) входит 3 000 галактик, среди которых самая яркая — галактика «Сомбреро». Скопление галактик — самогравитирующая, связанная группа. Это позволи­ло определить массу скопления, и полученные значения массы оказались больше, чем давала оценка их по светимостям, что при­вело к предположению о существовании «скрытой массы», при­рода которой пока не выяснена (т.н. темная материя).

Группу галактик составляют несколько десятков галактик. Раз­меры групп 0,1 — 1 Мпк, например, местная группа, состоящая из 38 галактик: нашей галактики Млечный Путь и огромной галак­тики туманность Андромеды (М32) со своими галактиками-спут­никами. Для нашей Галактики спутники — это находящиеся на расстояниях 165 000 св. лет и 200 000 св. лет Большое и Малое Магеллановы Облака и 14 карликовых галактик; у туманности Андромеды — это 5 больших и 5 малых галактик-спутников.

Галактики — динамически изолированные системы, состоя­щие из 10¹¹ звезд и светящиеся за их счет. Их зафиксировано сотни миллиардов. По внешнему виду галактики разделяют на эллипти­ческие (25 %), спиральные (50 %) и неправильные. Более яркие га­лактики являются и самыми массивными. Массы оцениваются по зависимости скорости их вращения от расстояния до центра. Уста­новлено, что массы большинства галактик (10⁹—10¹²) М_с (масс Солнца), а размеры составляют 1 —100 кпк. Помимо звезд, пыли и газа в галактики входят космические лучи и магнитные поля.

В центре многих галактик — яркое плотное ядро, как и у нашей Галактики. Это — галактики с активным ядром. Многие галактики активны в излучении коротковолновой области спектра; за него ответственны электроны, движущиеся в сильных магнитных по­лях. В радиодиапазоне активны N-галактики и сейфертовские галактики. Радиоизлучение огромной мощности исходит от наи­более удаленных объектов, излучающих также в УФ- и ИК-областях спектра. Их полное излучение по мощности сравнимо с излуче­нием целой галактики, потому их назвали квазарами, т.е. квази­звездами. Предполагают, что в центре у них находятся огромные черные дыры, взаимодействие с которыми вещества галактики и вызывают столь мощное излучение. Сейчас насчитывают более 24 тыс. квазаров. Для определения расстояний до галактик не применя­ют метод параллакса, так как они очень далеки. Используют наблю­дения цефеид, новых и сверхновых звезд, шаровых скоплений и пр.

Наша галактика — Млечный Путь — видна с Земли как поло­са на небе шириной 30°, средняя линия полосы определяет галак­тический экватор, плоскость которого образует с небесным эква­тором угол 62°. Этот вид отражает тот факт, что Галактика имеет форму диска, и Солнечная система находится вблизи экватори­альной его плоскости. Скорость вращения Галактики на расстоя­нии Солнца от центра около 220 — 250 км/с. В середине XX в. было установлено, что Галактика состоит из центрального взду­тия (балджа), окруженного дискообразной системой звезд, и га­лактической почти сферической короны — гало. Морфологичес­ки Млечный Путь имеет спиральную форму и спиральные рука­ва, как и туманность Андромеды, находящаяся от нас на расстоя­нии 2 млн св. лет. По названию созвездий, на которые проециру­ются спиральные рукава, выделяют рукав Киля- Стрельца (по на­правлению к центру Галактики), рукав Ориона-Лебедя (или Ме­стного рукава, так как Солнце находится вблизи его внутреннего края) и Персея (в направлении от центра). В направлении центра был обнаружен источник радиоизлучения (Стрелец-А), а в 2000 г. получены свидетельства того, что в самом центре Галактики на­ходится черная дыра массой 3М_с. Вещество в количестве 0,001 М_с выбрасывается за год вдоль оси вращения этого объекта со скоростью около 300 км/с. Эта ось наклонена к оси вращения Галактики под углом 41°, и она прецессирует с периодом в 2 300 лет. Интенсивное звездообразование отражает активность ядра Га­лактики. Период обращения Солнца вокруг центра около 200 млн лет. Он определен на основе скорости движения Солнца вокруг центра Галактики (240 км/с) и расстояния до него (7,1 — 8,9 кпк).

Скопления звезд — это группы звезд, расположенных близко друг к другу и связанных взаимным тяготением. Их разделяют на шаровые и рассеянные. В нашей Галактике около 150 шаровых и 1 540 рассеянных скоплений. Шаровые скопления (М13) — круг­лые образования, содержащие от нескольких десятков тысяч до миллиона звезд, состоят из старых объектов (до 10 млрд лет). Раз­меры шаровых скоплений около 100 пк, а масса (10⁵— 10⁷) М_с. Рассеянные скопления, состоящие из десятков и сотен более мо­лодых (1 — 2 млрд лет) звезд, находятся в плоскости Галактики. Так, одно из самых близких к нам скопление Плеяды (или Сто­жары) имеет возраст всего 60 млн лет. В созвездии Ориона сред­няя звездочка пояса кажется туманной — вокруг нее знаменитая туманность Ориона, где идет активно процесс звездообразования.

Звезда — «пространственно обособленная гравитационно-свя- занная непрозрачная для излучения масса вещества, в которой в значительных масштабах происходили, происходят или будут про­исходить термоядерные реакции превращения водорода в гелий». Такое определение дает астрофизик В. В. Иванов, характеризуя эту основную структурную единицу вещества мегамира. Кроме Солн­ца, все звезды от нас так далеко, что даже в телескопы выглядят светящимися точками разного блеска и цвета. Их характеристи­ки — светимость, масса и радиус находятся из наблюдений.

В зависимости от массы и возраста одна и та же звезда прохо­дит различные фазы эволюции. Конечные стадии эволюции приво­дят звезды в компактные формы — карлики, нейтронные звезды или черные дыры. Размеры (радиусы) их меняются от нескольких километров до нескольких тысяч километров (белые карлики), а у нормальных звезд — от 10⁸ м (почти солнечных) до 10¹¹ м (у сверхги­гантов). Ближайшая к Солнцу звезда находится в созвездии Цен­тавра (Проксима Центавра, или Кентавра) на расстоянии 4· 10¹³ км. Свет от этой звезды доходит к нам за 4 года и 3 месяца.

Солнце — центральное тело Солнечной системы: радиус Солн­ца 700 000 км, М_с ≈ 332 000 М₃, температура поверхности 6 • 10³ К, а в центре предполагают Т= 15 • 10⁶ К, поэтому там идут реакции превращения водорода в гелий. Солнце — звезда не первого по­коления, его возраст порядка 4,7 млрд лет. По количеству водоро­да и гелия можно оценить его срок жизни — еще 7 млрд лет. Преж­де чем Солнце превратится в белый карлик, оно некоторое время будет сиять как звезда красный гигант и резко увеличит светимость. Особенности Солнца связаны с наличием у него планетной систе­мы, поэтому двойника Солнца среди звезд пока не нашли.

Планетные системы существуют у других звезд, их открыто более 50, но разрешены не полностью, детальнее известны тела Солнечной системы: 9 больших планет и около 15 тыс. малых планет (астероидов). Есть убедительные аргументы в пользу существования планет за орбитой Плутона (за 39,6 а.е., или 10¹³ м), их пытаются обнаружить по их влиянию на движения объектов кометного облака Оорта. Воздействие Солнца доминирует над приливными силами Галактики внутри сферы радиусом около 300 000 а.е.

Расстояния в мегамире измеряют в световых годах (1 св. год ≈ 9,5 млрд км = 10¹⁵ м), а расстояние от Земли до Солнца, приня­тое за астрономическую единицу (1 а.е. = 150 млн км), свет пре­одолевает за 8,5 мин. Луна находится на расстоянии около 1 све­товой секунды, или 384 тыс. км, или 60 радиусов Земли. Попе­речник Солнечной системы — несколько световых часов, а бли­жайшая звезда (Проксима созвездия Центавра) находится на рас­стоянии около 4 св. лет.

Размеры планет определяют по наблюдениям за их движени­ями. Так, Меркурий — ближайшая к Солнцу планета — всегда находится близко к нему, при наблюдении с Земли его отклоне­ние (наибольшая элонгация) может быть до 23°, тогда как для Венеры (второй от Солнца) — 43 — 48°. Радиус орбиты Меркурия порядка 0,38 а.е. радиуса земной орбиты, Венеры — 0,7 а.е. Имея пропорции, можно построить примерную схему Солнечной сис­темы. Для получения абсолютных значений нужно знать хотя бы один радиус орбиты. Его можно определить с помощью радара. Сейчас все расстояния определены достаточно скрупулезно и раз­ными методами. Радиолокационные наблюдения позволяют с боль­шой точностью определить расстояния до небесных тел Солнеч­ной системы. Этим методом уточнены расстояния до Луны, Вене­ры, Меркурия, Марса, Юпитера.

2. Характеристики звезд

Звезды — это важнейшие объекты Вселенной. В них сосре­доточено до 95 % вещества Вселенной. Важнейшая наблюдае­мая характеристика звезд — количество приходящей от них энергии. Во II в. до н.э. Гиппарх ввел шкалу видимых звездных величин, используемую и поныне. Самые яркие — звезды (т = 1), самые слабые — (т = 6). В ее основе — освещенность Е_т, со­здаваемая источником, диапазон в 5 звездных величин соответ­ствует отношениям блеска в 100 раз, т.е. различие в I^т соответ­ствует отношению освещенностей, равному , т.е. (Е_т1)/(Е_т2) = 2,512^{- (m}₁^{- m}₂⁾ .

Это выражение удобно прологарифмировать, тогда получим ℓg(E_ml/E_m2) = - 0,4(m₁ -m₂), т.е. шкала видимых звездных вели­чин логарифмическая, в которой сравниваются освещенности, со­здаваемые источниками, причем она считается тем больше, чем слабее источник. Для Солнца т_с = -26^m,58, для полной Луны m_L = -12^m,7, поэтому из приведенной формулы можно заключить, что при одинаковой высоте над горизонтом полная Луна освещает земную поверхность в 465 000 раз слабее Солнца.

Для исключения влияния расстояния введено понятие абсо­лютной звездной величины М, которую имела бы звезда, нахо­дящаяся от нас на расстоянии 10 пк. М связана с т соотношени­ем, которое является одним из основных в звездной астроно­мии: М = т + 5 - 5ℓgr. Величину (т - М) называют модулем рас­стояния. Для Солнца абсолютная звездная величина М_с равна +4^m,72, т. е. существенно меньше, чем видимая, как для всех звезд, которые ближе 10 пк.

Расстояния до звезд (см. гл. 2) определяют методом параллак­са.

Звезды светятся, потому что их наружные слои разогреты до высоких температур, они светят собственным светом (в отличие от планет). Способность поверхности тела (планеты) отражать падающее на нее излучение характеризуется величиной, называе­мой альбедо. Альбедо определяется отношением яркости плоско­го элемента освещенной поверхности к яркости абсолютно белой поверхности. Так, для Земли альбедо — 40 %, для Луны — 7% и для Марса — 16 %.

Излучение звезд наблюдается в широком спектральном диапа­зоне, и чем выше температура, тем большая часть их спектра при­ходится на коротковолновую область. Излучение звезд подчи-

ня­ется законам термодинамики равновесного теплового излучения нагретых тел. В частности, к нему применимы: закон Стефана — Больцмана и закон смещения Вина. Закон Стефана—Больцмана говорит о суммарной энергии спектра излучения черного тела и имеет вид R = σT⁴, где σ = 5,7 • 10^{- 8} Вт/(м²· К⁴). Длину волны, на которой приходится максимум излучения черного тела, можно оп­ределить по закону смещения Вина: λ = b/Т, где b = 2,9·10 ^{- 3} м • К — постоянная Вина. Значит, энергия и спектр излучения звезды за­висят от температуры излучающего внешнего слоя — фотосферы.

Светимость звезд (L) — это полная мощность оптического излучения (количество световой энергии, выделяемой звездой за 1 с). Светимость звезд зависит от температуры и площади излуча­ющей поверхности. Ее выражают чаще в светимостях Солнца L_C, которую измеряют по приходящей от Солнца энергии, равной 3,8 • 10²⁶ Вт. Светимости звезд (10^{- 3}— 10⁶)L_C.

Поскольку для шара радиусом R площадь поверхности S = 4πR², для светимости звезды получаем L= σT⁴ 4πR² , где σ — по­стоянная Стефана—Больцмана. Записав такое же выражение для светимости Солнца L_C, можно получить отношение: (L/L_C) = = (T/T_C)⁴(R/R_C )². Таким образом, зная светимость и температуру звез­ды, можно вычислить ее радиус. Для Солнца радиус R_C определяет­ся из наблюдений по видимому угловому радиусу α, который состав­ляет около 16 угловых минут (см. зад. гл. 2): R_C = 1 а.е.· tgα ≈700 000 км. Для мира звезд Солнце имеет довольно скромный размер.

Масса звезд — важнейшая их характеристика, с которой свя­заны многие свойства звезды. Массу звезды непосредственно оце­нивают по ее гравитационному воздействию на другие тела. Мас­су Солнца, например, определяют по периодам обращения пла­нет, М_C ≈2 • 10³⁰ кг.

Независимые измерения масс и светимостей звезд показали, что светимости примерно пропорциональны четвертой степени массы. Тогда выполняется в относительных единицах приближен­ное равенство: (L/L_C) = (М/М_C)⁴ . Измерения показали, что звез­ды по своим массам отличаются не столь широко, как по свети­мостям. Можно сказать, что звезды большого размера имеют мас­сы не на много отличные от масс звезд средних светимостей, т.е. у гигантов и сверхгигантов из-за их больших размеров плотности малы, а у карликов, наоборот, очень велики.

В XIX в. звезды сначала рассортировали по размерам и мас­сам, а затем по спектрам. Спектры дают представления о хими­ческом составе звезд. Оказалось, что 98 % вещества — это водо­род и гелий, причем водорода (по массе) в 2,7 раза больше, чем гелия. Когда при истолковании спектров стали учитывать иони­зацию, стало возможным по спектральным сериям определять тем­пературу звезд.

2. Спектральные классы обозначены буквами латинского алфа­вита: О, В, A, F, G, К, М; каждый класс разбит на группы от 0 до 9. Имеются и дополнительные классы: для холодных звезд — R, N, S, для горячих — W. Звезды по светимости разделены на классы, обозначенные римскими цифрами: I — сверхгиганты, II — светящиеся гиганты, III — обычные гиганты, IV — подгиган-ты, V — звезды основной последовательности. Так что наше Сол­нце попало по спектру в G 2V.

Диаграмму зависимости светимостей звезд от их спектраль­ных классов (температур) составили голландец Эйнар Герцшпрунг и американец Генри Норрис Ресселл, она названа именами обоих. По оси абсцисс — спектральные классы звезд (показатели цвета или температуры), по оси ординат — светимости звезд L (или звездные величины М). Температуры и светимости звезд заключены в очень широких пределах. Причем эти характеристики зависимы.

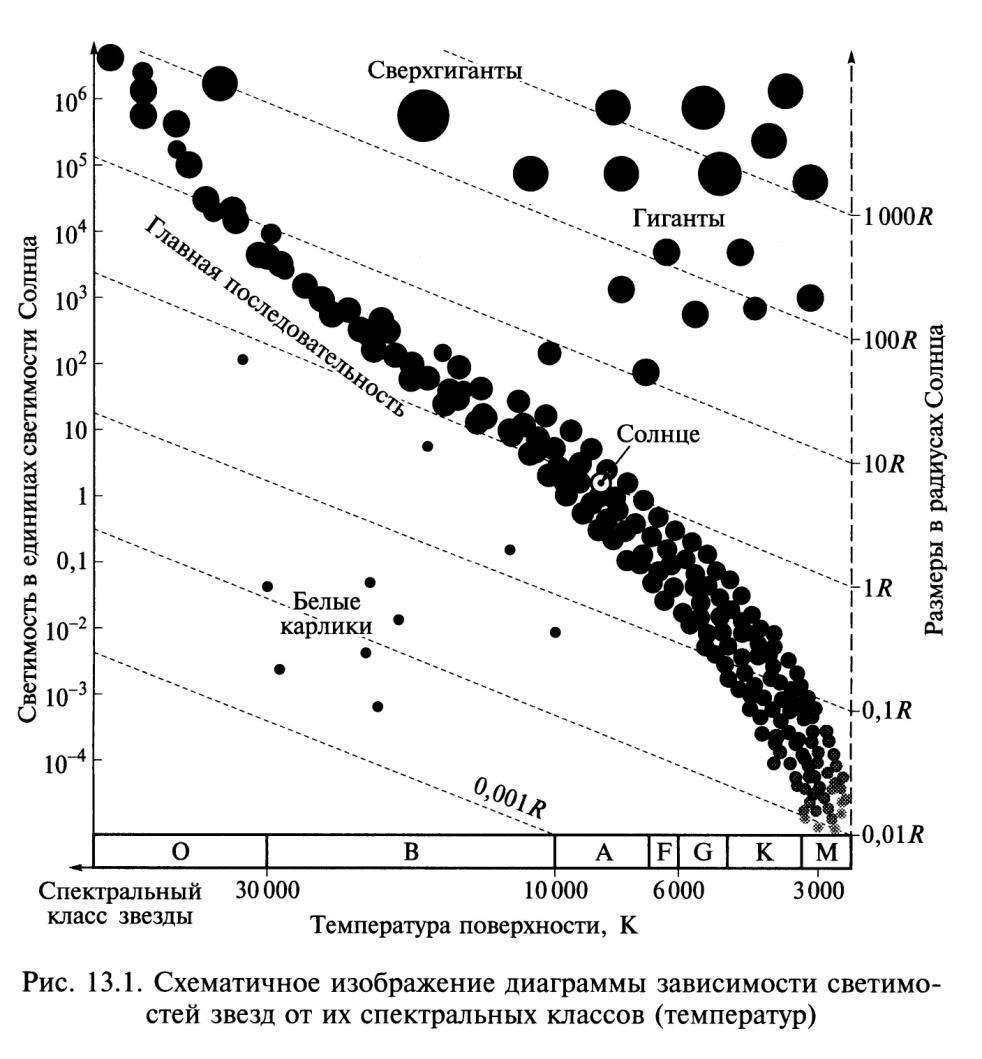
На диаграмме звезды располагаются не беспорядочно, а обра­зуют несколько последовательностей (рис. 13.1). Главная после- довательностъ — узкая полоса звезд, протянувшаяся из верхнего левого угла вниз. Так, вдоль нее сконцентрировано большинство звезд в окрестности Солнца. В правом верхнем углу — сверхги­ганты. Оказалось, что вблизи Солнца на одного сверхгиганта при­ходится около 1 000 гигантов и около 10 млн звезд Главной после­довательности. Группа звезд-гигантов компактна и расположена вверху диаграммы между Главной последовательностью и груп­пой сверхгигантов. Параллельно Главной последовательности, несколько ниже ее, расположены звезды, образующие последова­тельность субкарликов (у них содержание металлов гораздо ниже, чем у звезд Главной последовательности), в левом нижнем углу диаграммы — группа белых карликов, светимость которых мень­ше солнечной в сотни раз.