Сортировка выбором

При этом методе сортировки в неупорядоченной последовательности выбирается минимальный элемент, который исключается из дальнейшей обработки, а оставшаяся последовательность элементов принимается за исходную. Процесс повторяется до тех пор, пока все элементы не будут выбраны. Очевидно, что все выбранные элементы образуют упорядоченную последовательность.

Выбранный в исходной последовательности минимальный элемент размещается на предназначенном ему месте упорядоченной последовательности несколькими способами:

(а) минимальный элемент после i-го просмотра перемещается на i-е место (i=1,2,3,...) заданного массива, а элемент с i-го места - на место выбранного. После каждого просмотра упорядоченные элементы (от первого до элемента с индексом i) исключаются из дальнейшей обработки, т.е. размер каждого последующего обрабатываемого массива на единицу меньше размера предыдущего.

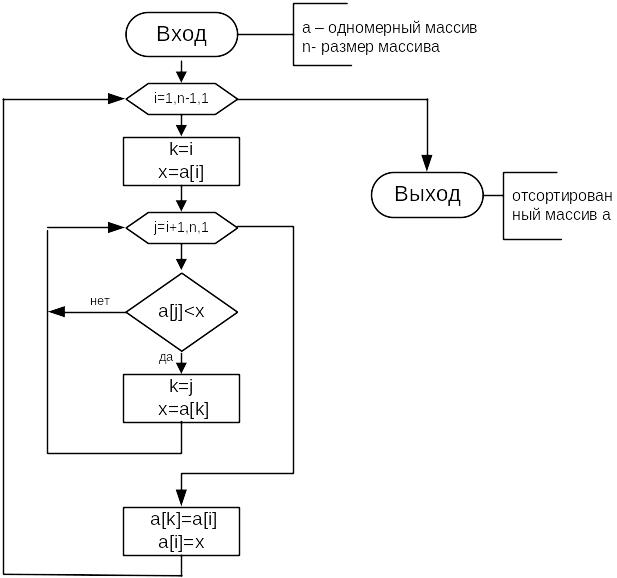
Блок-схема процедуры сортировки методом выбора

Числовой пример алгоритма:

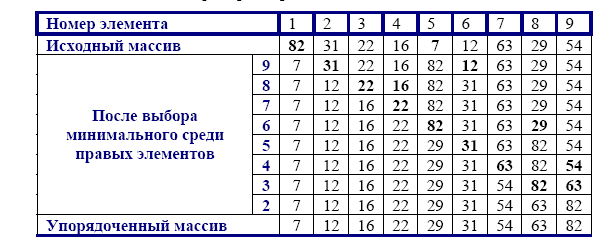
Общее число сравнений С и число пересылок (перестановок) М элементов:

Сортировка включениями

Сортировка методом прямого включения, так же, как и сортировка методом простого выбора, обычно применяется для массивов, не содержащих повторяющихся элементов.

Сортировка этим методом производится последовательно шаг за шагом. На k-м шаге считается, что часть массива, содержащая первые k-1 элемент уже упорядочена, то есть . Далее необходимо взять k-й элемент и подобрать для него место в отсортированной части массива такое, чтобы после его вставки упорядоченность не нарушилась, то есть надо найти такое что . Затем надо вставить элемент a[k] на найденное место.

С каждым шагом отсортированная часть массива увеличивается. Для выполнения полной сортировки потребуется выполнить n-1 шаг.

Осталось ответить на вопрос, как осуществить поиск подходящего места для элемента х. Поступим следующим образом: будем просматривать элементы, расположенные левее х (то есть те, которые уже упорядочены), двигаясь к началу массива. Нужно просматривать элементы а[j], j изменяется от k-l до 1. Такой просмотр закончится при выполнении одного из следующих условий:

• найден элемент а[j]<х, что говорит о необходимости вставки х между a[j-1] и a[j];

• достигнут левый конец упорядоченной части массива, следовательно, нужно вставить х на первое место.

До тех пор, пока одно из этих условий не выполнится, будем смещать просматриваемые элементы на 1 позицию вправо, в результате чего в отсортированной части будет освобождено место под х.

Блок-схема процедуры сортировки методом включения

Числовой пример алгоритма:

Общее число сравнений С и число пересылок (перестановок) М элементов:

Задание. Для сортировки методом включения

1. Изменить процедуру сортировки так, чтобы сортировка производилась по убыванию элементов.

2. Проверить, является ли данная последовательность целых чисел упорядоченной по убыванию. Если нет, упорядочить ее.

3. Отсортировать данный массив и подсчитать количество уникальных чисел в массиве.

4. Изменить процедуру сортировки так, чтобы значение параметра k с каждым шагом увеличивалось.

5. Отсортировать четные элементы массива с помощью простого выбора.

6. Отсортировать с помощью простого выбора элементы массива, стоящие на нечетных местах.

7. В массиве X(N) каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все единицы, затем все двойки и, наконец, все нули (дополнительного массива не заводить).

8. Составьте алгоритм, упорядочивающий элементы массива, стоящие на нечетных местах, в возрастающем порядке, а на четных - в убывающем.

9. В матрице n*m отсортируйте столбцы в порядке возрастания элементов k строки.

10. Даны список футбольных команд высшей лиги России и количество очков, набранных каждой командой в чемпионате России. Известно, что нет команд с равным числом очков. Распечатать список призеров.

11. В неупорядоченном массиве могут быть совпадающие элементы. Из каждой группы одинаковых элементов оставить только один, удалив остальные и «поджав» массив к его началу.

12. Из двух упорядоченных одномерных массивов (длины K и N) сформируйте одномерный массив размером K+N, упорядоченный так же, как исходные массивы.

13. Из двух упорядоченных одномерных массивов (длины K и N) сформируйте одномерный массив размером K+N, упорядоченный в обратную сторону.

14. Дан двумерный массив вещественных чисел размерностью [1..N,1..N]. Произвести сортировку столбцов по убыванию элементов последней строки. Вычислить сумму элементов расположенных на диагоналях полученной матрицы. Сортировку произвести методом прямого выбора. Вывести на экран исходный и полученный массивы в виде матрицы.