3 . Задачи и упражнения

Задачи

для самостоятельной работы

и работы в аудитории

1. Найдите направляющие векторы касательной, главной нормали и бинормали в произвольной точке бирегулярной кривой, если:

а) параметр на кривой является натуральным;

б) параметр на кривой не является натуральным.

2. Найдите нормальные векторы соприкасающейся, нормальной и спрямляющей плоскостей в произвольной точке бирегулярной кривой, если:

а) параметр на кривой является натуральным;

б) параметр на кривой не является натуральным.

3. Докажите, что кривая является отрезком прямой тогда и только тогда, когда ее кривизна равна нулю.

4. Найдите кривизну и кручение:

а) окружности;

б) винтовой линии.

5. Найдите кривизну в вершинах эллипса с полуосями a и b.

6. Докажите, что кривая лежит в плоскости тогда и только тогда, когда ее кручение равно нулю.

7. Докажите, что в вершине параболы кривизна достигает максимального значения.

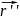8. Докажите, что кривая бирегулярна, если векторы и линейно независимы в каждой точке кривой.

9. Докажите, что кривизна графика функции вычисляется по формуле .

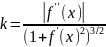10. Найдите кривизну и кручение следующих кривых:

1)

2)

3)

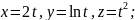
4)

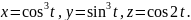
11. Найдите при каких a и b кручение кривой во всех точках равно ее кривизне.

12. Найдите точки на кривой 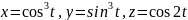, в которых кривизна имеет минимальное значение (локальное).

13. В каких точках радиус кривизны кривой

достигает локального минимума?

14. Докажите, что следующие кривые плоские, и составьте уравнения плоскостей, в которых расположены их образы:

1)

2)
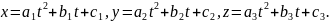