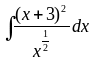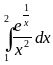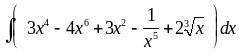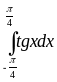Вариант 5

1. Найти интегралы, используя свойство линейности:

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)

2. Найти интегралы методом подстановки:

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)
13)	14)

3. Интегрирование по частям:

1)	2)
3)	4)
5)	6)
7)

4. Найти интегралы:

1)	2)
3)	4)

5. Найти интегралы от рациональных дробей:

1)	2)
3)

6. Вычислить интегралы:

1)	2)
3)	4)
5)

7. Вычислить площадь плоской фигуры, ограниченной линиями:

а) у = 8 + 2х - х², у = 2х + 4

б) у = (х + 1)², у² = х + 1

в)

8. Вычислить объемы тел, образованных вращением фигур, ограниченных линиями:

а) вокруг ОУ

б) вокруг ОХ

9. Вычислить площадь поверхности, образованной вращением вокруг оси абсцисс кривой у² = х - 3, отсеченной прямой х = 5.

Вариант 6

1. Найти интегралы, используя свойство линейности:

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)

2. Найти интегралы методом подстановки:

1)	2)
3)	4)
5)	6)
7)	8)
9)	10)
11)	12)
13)	14)
15)

3. Интегрирование по частям:

1)	2)
3)	4)
5)	6)
7)

4. Найти интегралы:

1)	2)
3)

5. Найти интегралы от рациональных дробей:

1)	2)
3)

6. Вычислить интегралы:

1)	2)
3)	4)
5)

7. Вычислить площадь плоской фигуры, ограниченной линиями:

а) y = ln x, x = e и осью абсцисс

б) у² = 2рх, х² = 2ру

в)

8. Вычислить объемы тел, образованных вращением фигур, ограниченных линиями:

а) у = Sin x, x = 0, x = , y = 0, вокруг оси ОУ

б) одной аркой циклоиды и осью ОХ;

вокруг оси ОХ.

9. Вычислить площадь поверхности, образованной вращением вокруг оси абсцисс кривой одной полуволны синусоиды

y = Sin x вокруг оси ОХ.