2.2. Различные модификации метода Эйлера
Для получения более точной формулы нужно точнее аппроксимировать интеграл в правой части.
Воспользуемся квадратурной формулой трапеции, получим
,
или иначе,
.
Заменим
в правой части полученной формулы на
некоторую величину
.
Тогда правая часть изменится на величину
(
находится между
и
).
Таким образом, имеет место соотношение
.
Условию
удовлетворяет результат вычислений по
формуле Эйлера
.
Эти соотношения определяют пару расчетных
формул:
(2.4)
Рассмотренный метод носит название метода Эйлера-Коши.
Построим другую пару формул с погрешностью на шаге того же порядка. Интеграл в правой части (2.3) заменим по формуле средних прямоугольников:
,
или
.
Если
,
то, как и в предыдущем случае, имеем
.
В качестве
можно взять результат вычислений по
формуле Эйлера с шагом
:
.
Этим соотношениям соответствуют пара
расчетных формул, определяющих еще одну
модификацию метода Эйлера:
(2.5)
2.3. Оценка погрешности по правилу Рунге
Пусть
и
решения задачи Коши, полученные с шагами
и
.
Тогда в совпадающих узлах, имеет место,
приближенное равенство:
,
где
для метода Эйлера и
для рассмотренных его модификаций.
На практике
применяют следующий метод: выбрав из
каких-либо соображений шаг интегрирования
,
проводят вычисления с шагом
и
и сравнивают результаты. Если в общих
точках
,
где
- заданная точность, то считают, что шаг
удовлетворяет заданной точности. В
противном случае проводят вычисления
с шагами
и
и т.д.
2.4. Выполнение лабораторной работы по численному решению задачи Коши в среде MathCad
Целью работы является укрепление знания студентов по численным методам решения задачи Коши для обыкновенного дифференциального уравнения на основе проведения экспериментальной исследовательской работы.
Лабораторная работа состоит из двух заданий. В первом задании, выполняемом дома, студент должен численно решить задачу Коши одним из предлагаемых ему методов с заданным шагом и оценить погрешность по методу Рунге. Второе задание выполняется в компьютерном классе и состоит оно в численном решении задачи Коши с заданной точностью. Разберем пример. Пусть требуется численно решить задачу Коши:
на отрезке
с шагом
методом Эйлера - Коши.
Решение. По методу Эйлера – Коши, имеем
где
.
Следовательно,
получаем
Для оценки
погрешности численно решаем задачу
Коши с шагом
:
Таким образом, решение полученное с шагом , найдено с точностью
.
Второе задание – это численное решение задачи Коши с заданной точностью . Соответствующий этому заданию документ MathCad представлен в листингах 2.1 и 2.2. Представлен так же график решения.
Листинг 2.1. Метод Эйлера – Коши с автоматическим выбором шага
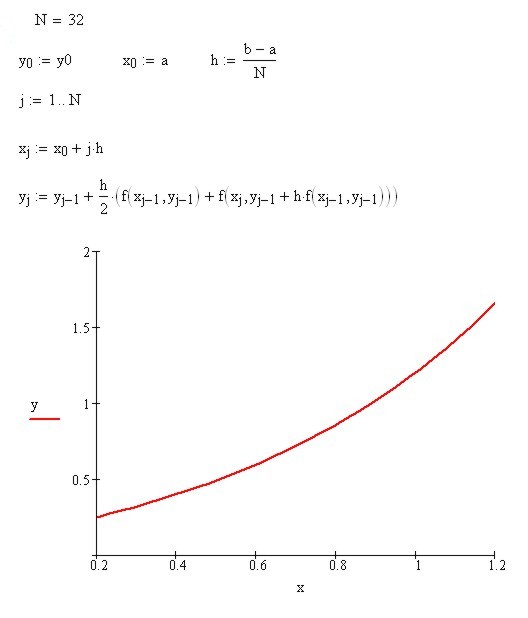
Листинг 2.2. Продолжение лабораторной работы
Литература
Демидович Б.П., Марон И.А. Основы вычислительной математики. – Наука, 1966;
Калиткин Н.Н. Численные методы. – М.: Наука 1978;
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 1987.
ЗАДАЧИ
Вычисление интеграла одним из пяти методов: метод левых прямоугольников, метод правых прямоугольников, метод средних прямоугольников, метод трапеций, метод Симпсона с оценкой погрешности по методу Рунге.
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Решить задачу Коши
на отрезке
.
Для всех вариантов
.
.
.
.
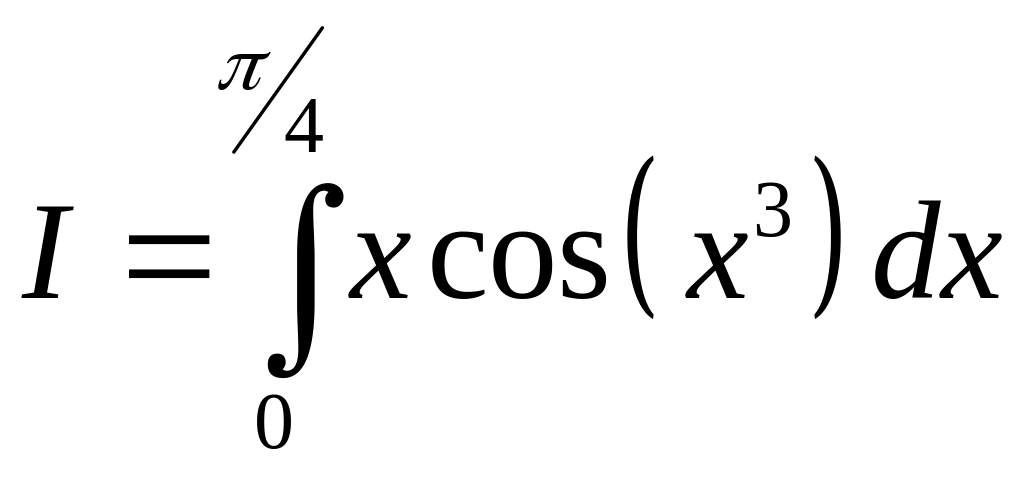