Выполнение первой части лабораторной работы по теме «Численные методы решения нелинейных уравнений и систем»
Вторая лабораторная работа посвящена численным методам решения нелинейных алгебраических уравнений и систем уравнений. Работа состоит из двух частей. В первой части студент одним из предлагаемых ему методов находит приближенное значение корня нелинейного уравнения с использованием среды MathCad.
Пусть
дано уравнение
.
Требуется найти приближенное значение
корня на отрезке
методом дихотомии с точностью
.
Заметим, что функция
непрерывна на указанном отрезке и строго
возрастает на нем. Так как
,
то на отрезке
данное уравнение имеет единственный
корень. Пример поиска корня уравнения
методом дихотомии иллюстрируется
листингом 3.1.
Найдем теперь
корень данного уравнения методом хорд.
Для этого заметим, что функция
дважды непрерывно дифференцируемая на
отрезке
.
Кроме того, на этом отрезке выполняются
неравенства
.
Поэтому последовательность, сходящаяся
к корню имеет вид:
.
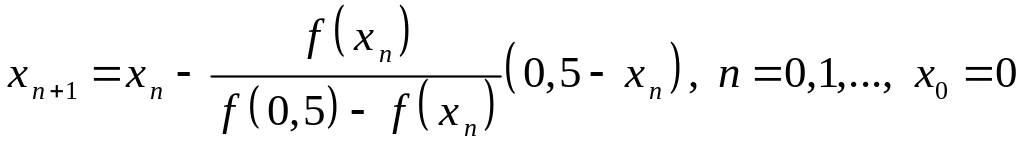Так как на отрезке
выполняется неравенство
,
то приближенным значением корня будет
элемент последовательности
,
для которого выполняется неравенство
.
Пример поиска корня уравнения методом
хорд иллюстрируется листингом 3.2.
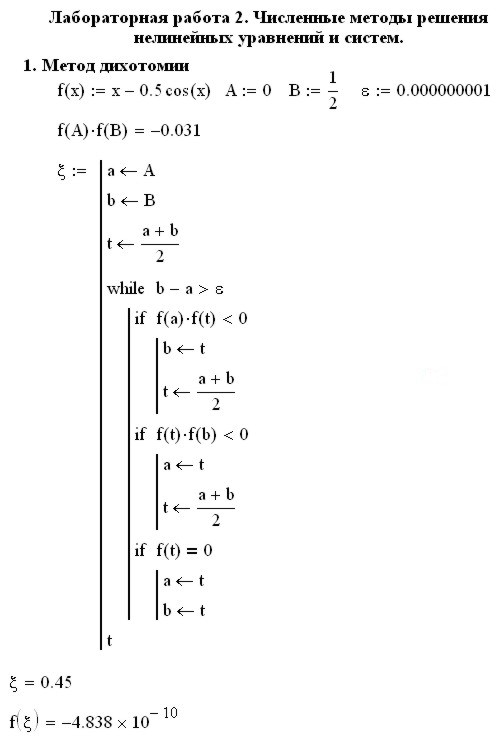
Листинг 3.1. Поиск корня уравнения методом дихотомии
Листинг 3.2. Поиск корня уравнения методом хорд
Рассмотрим теперь
решение уравнения методом итераций.
Для этого перепишем его в виде
и заметим, что функция
на отрезке
удовлетворяет следующим условиям:
,
для любого
выполняется
,
.
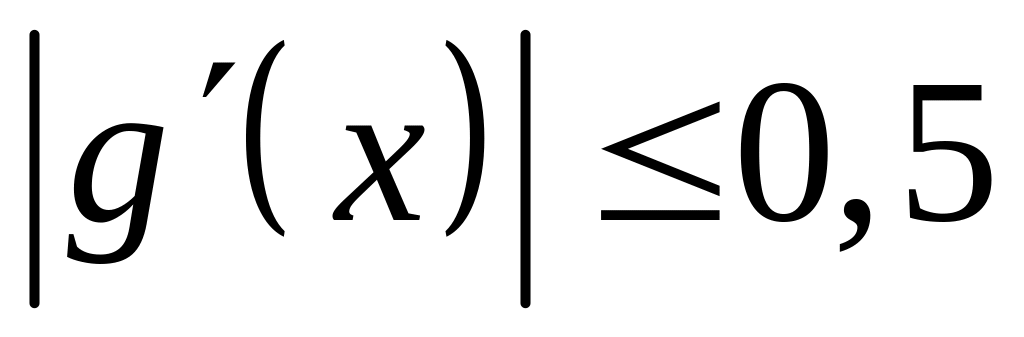Следовательно,
последовательность
сходится к корню
уравнения и имеет место неравенство
.
Пример поиска корня уравнения методом итераций иллюстрируется листингом 3.3.
Листинг 3.3. Поиск корня уравнения методом итераций.
Глава 4. Решение систем нелинейных уравнений
Систему нелинейных
уравнений с
неизвестными можно записать в виде
или, более кратко,
в векторной форме
,
где
и
.
Ведем следующее обозначение
.
Мы будем считать,
что в пространстве
задана норма в виде
.
Тогда, согласованная с ней норма матрицы
имеет вид
.
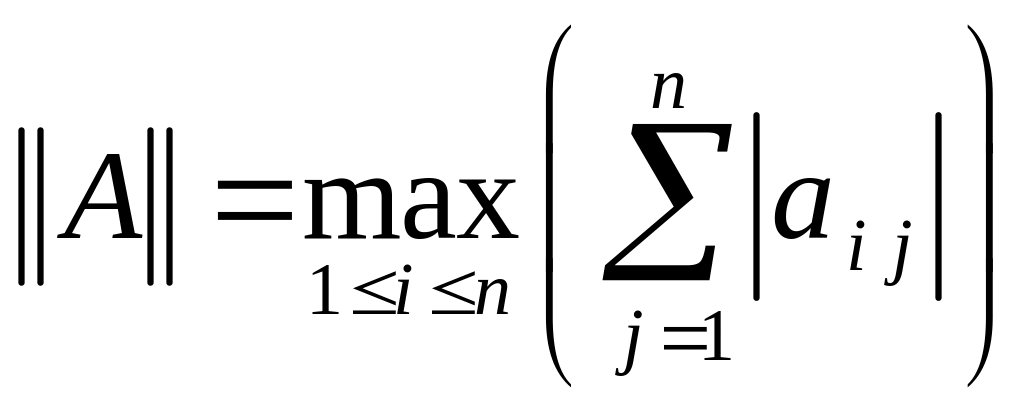В данной главе мы
рассмотрим некоторые методы решения
нелинейных систем уравнений.
1. Метод итераций
Рассмотрим систему нелинейных уравнений специального вида
, (4.1)
где
.
Решение системы (4.1) будем искать как
предел последовательности
,
где
.
Теорема 4.1.
Пусть функции
действительны, определены и непрерывны
вместе со своими частными производными
первого порядка в некоторой замкнутой
ограниченной области
,
причем
для всех
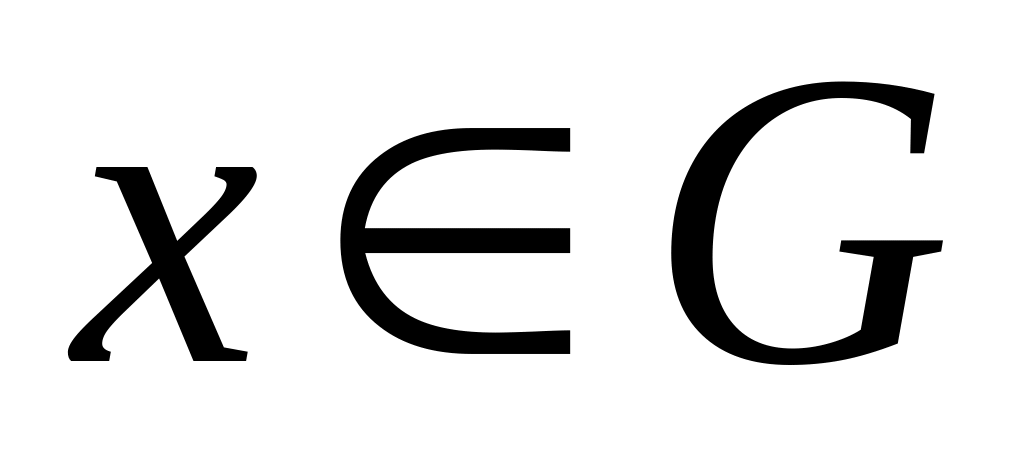выполняется
;
.
Тогда последовательность
сходится при любом выборе начального
приближения
,
и предельный вектор
является в области
единственным решением системы (4.1). Кроме
того, имеет место неравенство
. (4.2)
Как было сказано в главе 3, лабораторная работа по теме «Численные методы решения нелинейных уравнений и систем» состоит из двух частей. Во второй части работы требуется найти приближенное решение системы с заданной точностью.
Пример. Найти приближенное решение системы
в квадрате
с точностью
.
Решение. Перепишем систему в виде:
Пусть
.
Введем функции
.
Запишем матрицу Якоби этой системы функций:
.
Тогда
Так как при любом
имеем
,
то в квадрате
существует единственное решение
данной системы. При этом
,
где
.
Положим
,
тогда
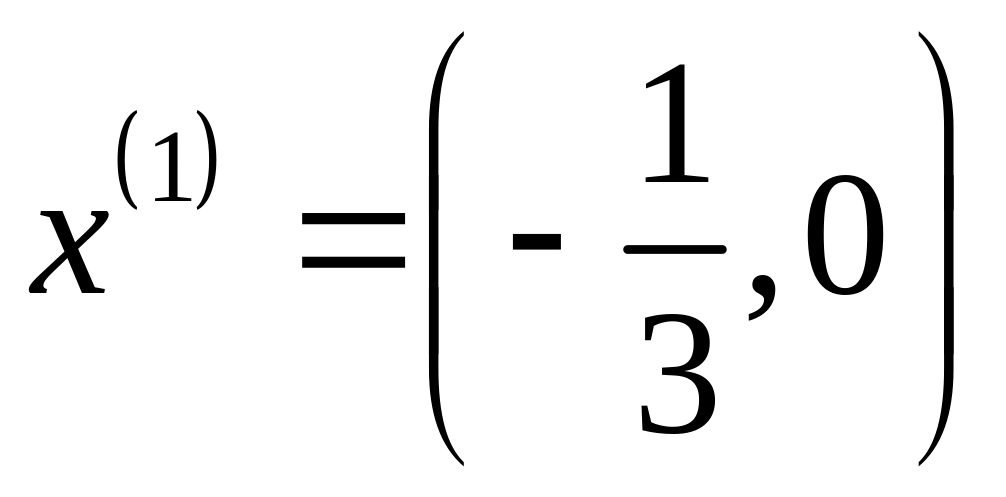и
.
Следовательно, последнее неравенство
для определения количества итераций
запишется в виде:
.
Решая данное
неравенство, получаем
.
Итак,
является приближенным решением системы,
удовлетворяющим заданной точности. В
листинге 4.1 приведен документ MathCad,
в котором реализован метод итераций.
Листинг 4.1. Метод итераций