3.3. Метод хорд

Предположим, что функция в уравнении (3.1) удовлетворяет следующим условиям:

• ;

• для любого .

Остальные случаи для знаков производных разбираются аналогично. Обозначим через корень уравнения (3.1).

Метод хорд состоит в следующем. График функции заменяется его хордой, т.е. отрезком, соединяющим точки (рис. 3.1). Абсцисса точки пересечения этой хорды с осью и рассматривается как первое приближение искомого корня.

Рис 3.1. Решение уравнения по методу хорд

Уравнение хорды имеет вид . Его можно переписать в виде . Обозначим правую часть этого уравнения через . Решая уравнение , находим .

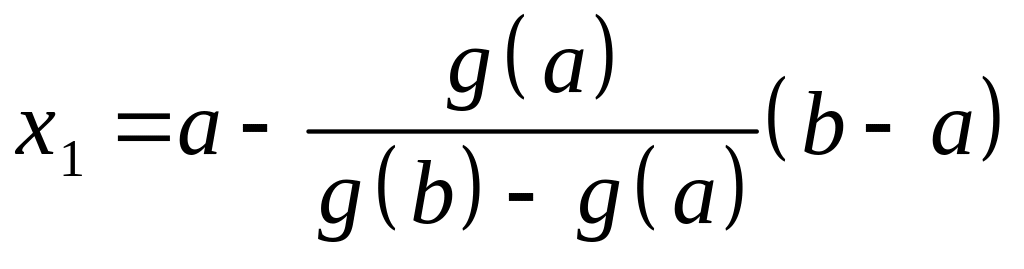Так как , то . Действительно, и, кроме того, . Так как , то функция выпукла вниз, следовательно, любая внутренняя точка хорды, соединяющей крайние точки графика функции , лежит над соответствующей точкой графика функции , т.е. . Поэтому, . Так как , то, в силу возрастания функции , получаем, что .

Снова проводим хорду через точки и находим

.

Продолжая описанный процесс, получим ограниченную монотонно возрастающую последовательность , где

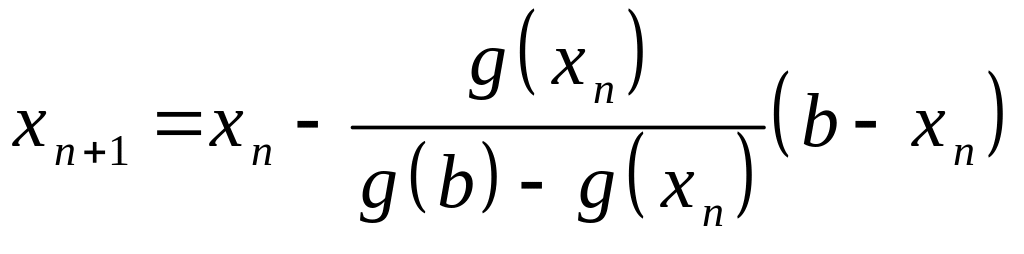. (3.4)

Так как последовательность возрастает и ограничена сверху, то существует предел . Переходя к пределу в равенстве (3.4), получим . Таким образом, последовательность сходится к корню уравнения (3.1).

Предположим, что . Тогда, по теореме Лагранжа, получим

.

Отсюда

. (3.5)

Неравенство (3.5) дает оценку погрешности приближенного корня.

4. Метод Ньютона

Предположим, что функция снова удовлетворяет таким же условиям, как и в методе хорд. Проведем касательную к графику функции в точке . Абсцисса точки ее пересечения с осью и считается первым приближением корня уравнения (7). Уравнение касательной имеет вид:

.

Рис. 2. Решение уравнения по методу Ньютона

Обозначим его правую часть через . Решение уравнения имеет вид . По предположению, функция строго возрастает и выпукла на , следовательно, . Таким образом, . Так как , то . К отрезку применяем аналогичные рассуждения. Имеем . Проводим касательную через точку и находим точку пересечения этой касательной с осью . Продолжая описанный процесс, получим последовательность такую, что

. (3.6)

Эта последовательность монотонна и ограничена снизу, поэтому существует предел . Переходя к пределу в равенстве (3.6), получим .

Дадим еще оценку скорости сходимости метода Ньютона. Пусть для рассматриваемой функции на рассматриваемом интервале выполняются неравенства

.

Разложим функцию в окрестности точки по формуле Тейлора, например, с остаточным членом в форме Лагранжа

,

где . Если то, подставляя в написанную формулу, получим

.

Отсюда

,

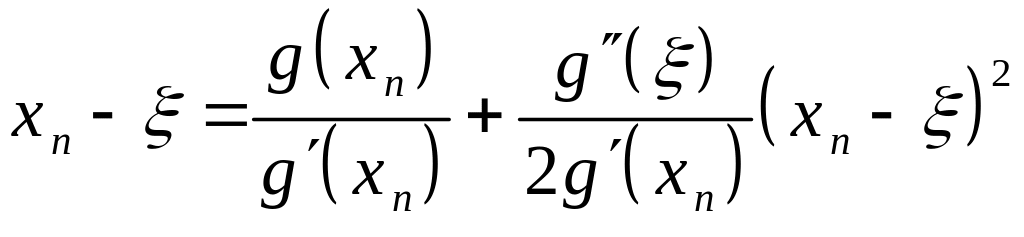или, в силу формулы (12), получим

.

Следовательно,

,

откуда

.

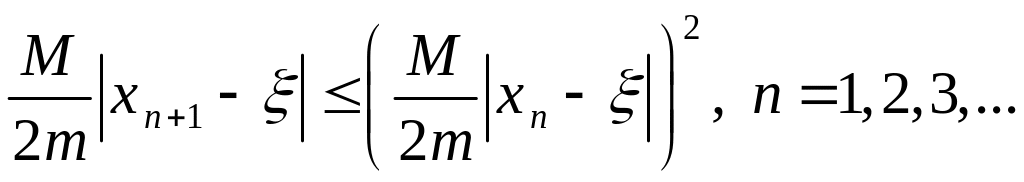Применяя последовательно это неравенство, будем иметь

Если выбрать первоначальное приближение так, чтобы , то получим

.

Таким образом, скорость сходимости приближенных решений к корню значительно превышает скорость убывания геометрической прогрессии со знаменателем по абсолютной величине, меньшим единицы.