Глава 2. Выполнение лабораторной работы по

Z - ПРЕОБРАЗОВАНИЮ В СРЕДЕ MATHCAD

Цель выполнения лабораторной работы состоит в том, чтобы познакомить студента с применением z-преобразования к решению линейных разностных уравнений с постоянными коэффициентами и систем. Кроме этого, показать некоторые приемы использования среды MathCad в решении в символьном виде, возникающих в этих задачах систем линейных уравнений, а также преобразовании выражений.

2.1. Решение линейных разностных уравнений с постоянными коэффициентами с использованием среды MathCad

Эта часть работы выполняется в два этапа. Первый этап выполняется дома, а второй в дисплейном классе.

Этап 1. По данному линейному разностному уравнению с постоянными коэффициентами составить преобразование Лорана последовательности – оригинала . Определить особые точки функции и классифицировать их.

Этап 2. Выполняется в дисплейном классе. По найденному на первом этапе преобразованию Лорана последовательности находим саму последовательность, вычисляя вычеты функции в особых точках с использованием MathCad. Далее выполняем проверку, преобразуя получаемые выражения с использованием MathCad.

Рассмотрим пример выполнения первой части первой лабораторной работы.

Лабораторная работа 1. Часть 1. Решить разностное уравнение с постоянными коэффициентами с использованием z-преобразования:

;

.

Порядок выполнения. Найдем сначала изображение оригинала . Согласно таблице 1, имеем . Следовательно, по теореме о дифференцировании изображения, получаем:

;

Применяя z-преобразование к данному уравнению и используя теорему опережения, находим:

.

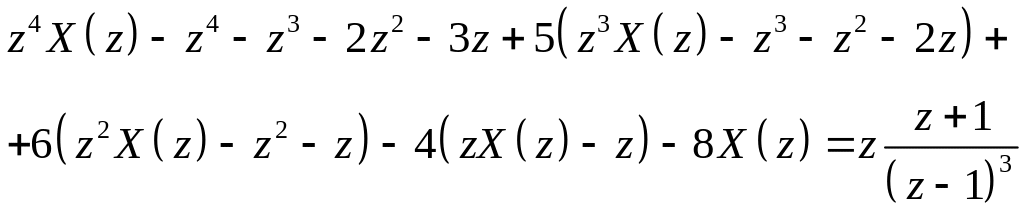Отсюда получаем изображение:

.

Дальнейшее выполнение работы осуществляем с использованием среды MathCad. Во-первых, необходимо получить разложение знаменателя на множители. Осуществляется это действие с помощью команды меню Symbolics → Factor (разложить многочлен можно и без использования MathCad). В результате изображение мы представим в следующем виде:

.

Как легко видеть, особыми точками данной функции будут - полюс третьего порядка и - полюс четвертого порядка. Используя теорему о нахождении вычета функции в полюсе, получаем

.

Указанные пределы находим с использованием MathCad. Для проверки получаем последовательность-оригинал с помощью встроенного в MathCad метода обращения z-преобразования. Для этого нажатием клавиш [Ctrl]+[Shift]+[.] создаем поле ввода (▪▪→) и набираем в нем X(z) invztrans, z. Ниже приведен документ MathCad, в котором реализовано выполнение первой лабораторной работы. Ответом к данной работе будет найденная последовательность оригинал:

.

Подставляя в уравнение и используя команду Symbolics → Expand, убеждаемся в правильности найденного решения.

2.2. Решение систем линейных разностных уравнений с постоянными коэффициентами с использованием среды MathCad

Также как и первая часть лабораторной работы, вторая часть выполняется в два этапа. На первом этапе по данной системе находим изображения последовательностей, входящих в систему. Этот этап осуществляется дома. На первом этапе определяем особые точки изображений и классифицируем их.

Второй этап выполняется в компьютерном классе. По полученным изображениям определяем, используя MathCad, последовательности – оригиналы. На этом же этапе осуществляем проверку найденных решений. Рассмотрим пример выполнения второй части первой лабораторной работы.

Лабораторная работа 1. Часть 2. Решить систему линейных разностных уравнений с постоянными коэффициентами с использованием z-преобразования

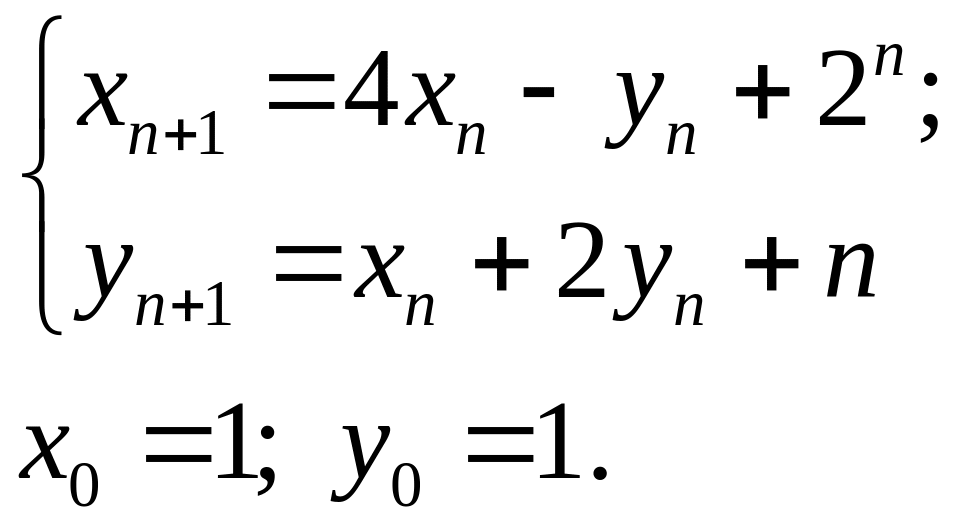
Порядок выполнения. Переходим к изображениям по Лорану. Используя таблицу 1, находим

Перепишем систему в виде:

(2.1)

Для ее решения используем метод решения системы в символьном виде, предусмотренный в MathCad. Систему необходимо указать после ключевого слова Given. При задании системы нужно использовать знак равенства из вкладки Boolean панели инструментов. Решение системы мы получим после команды .

После решения системы необходимо разложить знаменатели полученных дробей на множители с помощью команды Symbolics → Factor. Далее определяем особые точки функций и классифицируем их тип. После чего находим последовательности – оригиналы по формулам

, ,

где суммирование происходит по всем особым точкам функций и соответственно.

Итак, разберем нахождение последовательностей в MathCad по действиям.

Действие 1. Решаем систему (2.1) в символьном виде:

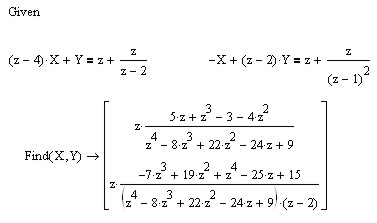
Действие 2. Разложим знаменатели полученных дробей на множители:

Действие 3. В результате предыдущих действий мы получили изображения по Лорану последовательностей :

.

Как легко видеть, функция имеет особые точки: - полюс второго порядка, - полюс второго порядка. Функция имеет особые точки - полюс первого порядка, - полюс второго порядка, - полюс второго порядка. Находим последовательности и :

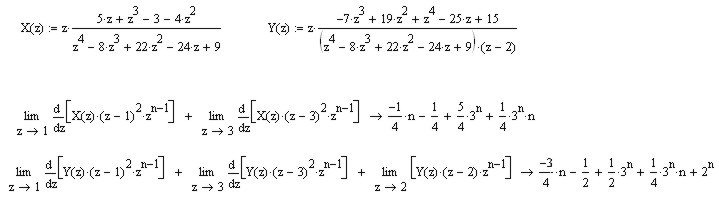
Таким образом, искомые последовательности:

.

Действие 4. Выполним проверку найденных решений, используя команду Symbolics → Expand: