1.2. Решение линейных разностных уравнений с постоянными коэффициентами и систем уравнений с помощью z - преобразования
Линейным разностным уравнением с постоянными коэффициентами называется уравнение вида
. (1.4)
Число
называется порядком уравнения.
Для того чтобы
решение уравнения получалось вполне
определенным, должны быть заданы
начальные условия
.
В этом случае, полагая в уравнении (1.4)
,
мы сможем найти
.
Затем, полагая в уравнении
,
мы сможем найти
и т.д. Следовательно, все значения
могут быть вычислены последовательно.
Поэтому уравнение (1.4) называют еще
рекуррентным
уравнением.
Мы пойдем по другому пути – получим для
общую формулу. Проще всего это сделать
при помощи z
– преобразования.
Обозначим
преобразование Лорана решения
уравнения (1.4), а
- преобразование Лорана последовательности
.
Из теоремы опережения следует
.
Поэтому разностное уравнение (1.4) после z – преобразования переходит в изображающее уравнение
.
Из полученного уравнения находим
.
Оригинал
,
соответствующий полученному изображению
,
будет удовлетворять уравнению (1.4) и
заданным начальным условиям. Сам оригинал
можно искать в виде
,
где сумма распространяется на все особые точки функции .
Пример. Найти решение уравнение
,
удовлетворяющее начальным условиям
.
Решение. Используя теореме опережения и таблицу 1.1, находим изображающее уравнение
.
Решая его относительно
,
получаем
.
Особыми точками
полученной функции являются
- полюс второго порядка и
- полюс первого порядка. Следовательно,
.
.
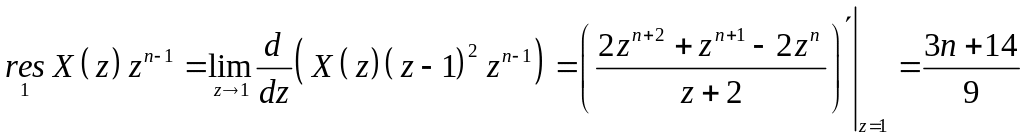Итак, решение уравнения имеет вид
.
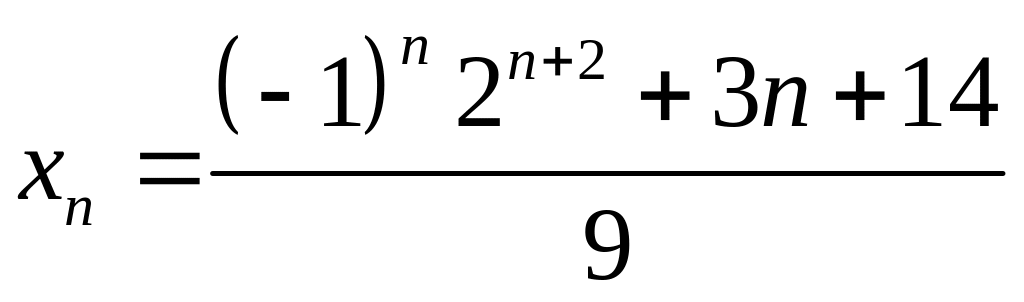Рассмотрим теперь
решение систем линейных разностных
уравнений с постоянными коэффициентами.
Заметим, что последовательность –
оригинал представляет собой функцию
целочисленного аргумента, для которой
.
Такое обозначение даст возможность не
использовать двойные индексы.
Система линейных разностных уравнений с постоянными коэффициентами может быть записана в виде:
(1.5)
Начальные условия
для определения решения данной системы
запишем в виде:
.
Применим операционный метод к решению этой системы. Пусть
;
.
Используя теорему опережения и начальные условия, находим
.
Таким образом,
применяя z-преобразование
к системе (1.5), получаем систему линейных
неоднородных уравнений относительно
неизвестных
.
Решив эту систему и найдя оригиналы для , получим решение систему (1.5).
Пример. Решить систему разностных уравнений:
Решение. Переходя к изображениям по Лорану, получаем
Полученную систему перепишем в виде
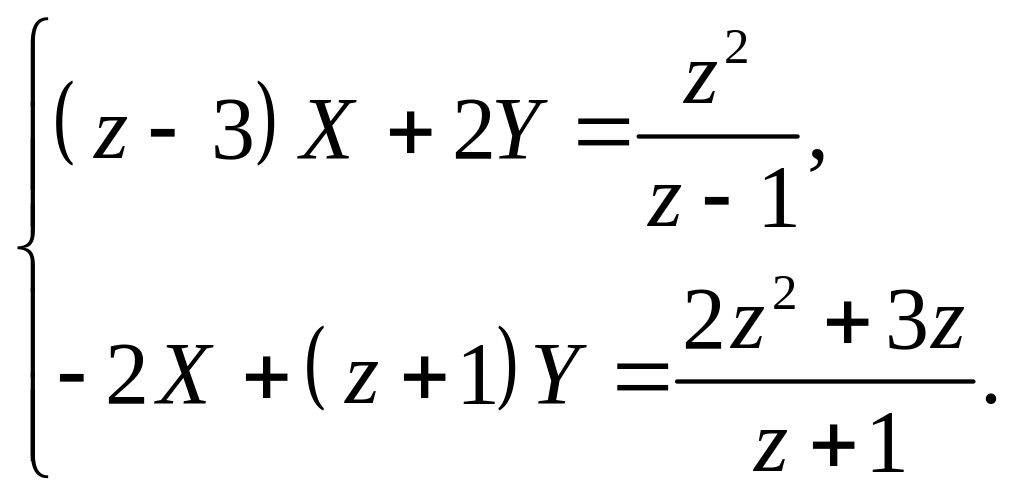
Решая систему по правилу Крамера, находим
;
.
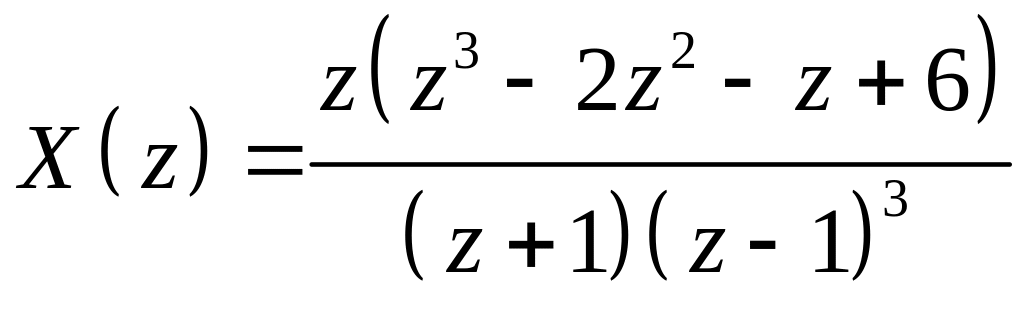Особыми точками
полученных функций являются
- полюс первого порядка и
- полюс третьего порядка. Поэтому
.
Заметим, что линейное разностное уравнение можно свести к системе линейных разностных уравнений. Действительно, пусть дано уравнение (1.4). Обозначим
.
Очевидно, что
.
Из уравнения (1.4) следует, что
.
Мы, таким образом, приходим к системе
