§26. Поверхностная плотность зарядов на границе раздела двух поляризованных диэлектриков.

Условия на границе получаются из некоторых дифференциальных выражений.

Уравнение Максвелла

на границе раздела:

и связаны со свободным зарядом. Заряды, связанные с веществом учли в индукции .

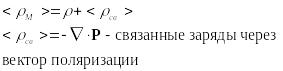
Пусть - свободные заряды отсутствуют. Рассмотрим заряды, возникающие при поляризации вещества.

обозначим

У этого уравнения такой же вид как и у . Применим к нему теорему Остроградского-Гаусса (так же как и для получения скачка на границе), тогда:

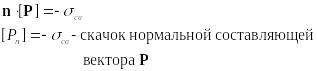
- связанный заряд, приходящийся на единицу площади поверхности раздела.

Если имеется область заполненная диэлектриком, находящимся в вакууме, то:

Здесь - внешняя нормаль.

Пусть дан шар – однородно поляризованный диэлектрик с поляризацией

В точке :

§27. Электрический дипольный момент поляризованного диэлектрика. Роль поверхностных зарядов.

Дипольный момент

Здесь учитываем, что есть и объёмные и поверхностные заряды.

Если не учитывать свободные заряды, тогда:

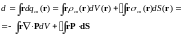
Рассмотрим второе слагаемое:

Здесь - скаляр, а - вектор, который даёт векторное представление всему интегралу. Применим теорему Остроградского-Гаусса (т.е. ):

В этом интеграле два слагаемых:

Тогда:

Пусть

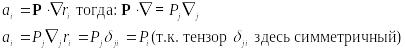
В результате примет вид:

Здесь - вектор поляризации.

§28. Электрическое поле поляризованного диэлектрика. Поле диполя.

Запишем потенциал, создаваемый некоторым распределением заряда:

Подставим плотности и пусть - дифференцирование ведётся по :

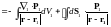
Применим ко второму слагаемому теорему Остроградского-Гаусса:

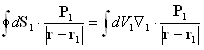
Тогда:

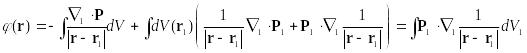
И мы получаем:

Если мы имеем диполь:

Для распределения диполя

-для распределения заряда

Вектор поляризации – объёмная плотность дипольного момента. Тогда для точечного диполя:

- по нему интегрируем, - точка в которую помещён источник.

Если , т.е. диполь находится в начале координат, то:

§29. Случай однородно-поляризованного диэлектрика.

по величине и по направлению постоянен в рассматриваемой области.

Запишем дипольный момент этого диэлектрика:

Здесь - константа.

Найдём потенциал, который создаёт однородно-поляризованный диэлектрик:

, где - интеграл-вектор:

Результат интегрирования зависит от формы поверхности.

Результат так же зависит от местонахождения точки (внутри объёма или вне объёма).

Для точки, принадлежащей объёму, например эллипсу:

, где - тензор, определяемый формой области, по которой производится интегрирование. - тензор деполяризации. Тензор для таких областей:

тогда . Для трехосного эллипсоида тензор можно представить в виде матрицы:

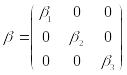
След этой матрицы .

Если область в виде шара, то все направления одинаковы, т.е. и тогда:

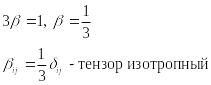
Если область – бесконечный цилиндр и если 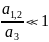, тогда и им можно пренебречь. Тогда . В круговом сечении (если цилиндр круговой), т.е. при : .

Примечание:

П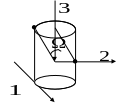 усть есть цилиндр. - телесный угол, он примерно определяет здесь, например, значение (при умножении на ).

Если область – сплющенный эллипсоид, т.е.

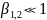, то , тогда .

С помощью потенциала можно найти напряжённость:

Это напряжённость поля однородно-поляризованного диэлектрика внутри объёма этого диэлектрика, т.е. .

Если диэлектрик находится во внешнем поле, то чтобы найти внутреннее поле такого диэлектрика надо к ещё прибавить внешнее поле , где - однородное внешнее поле.