§8. Микро и Макро уравнения Максвелла для электромагнитного поля в среде.
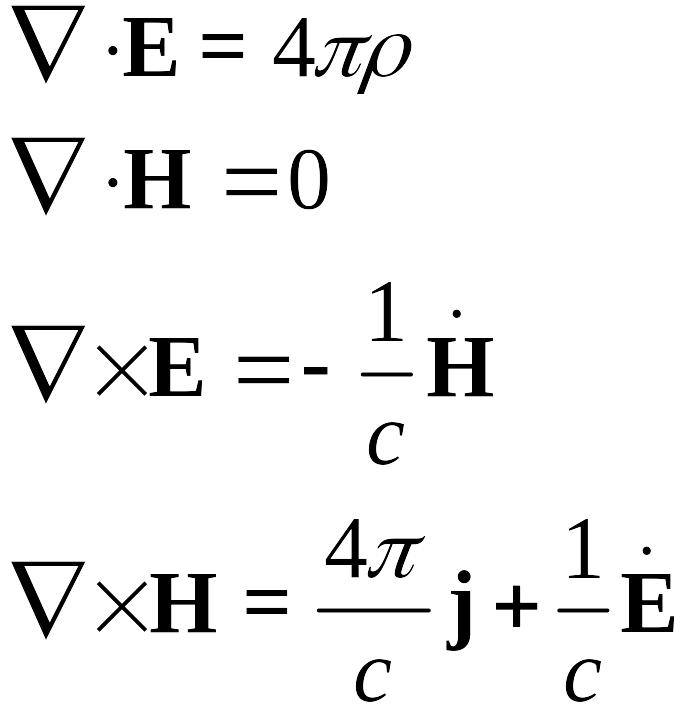
С помощью этих уравнений можно описывать
электромагнитное поле в среде. В среде
будем ставить индекс «
»=микро
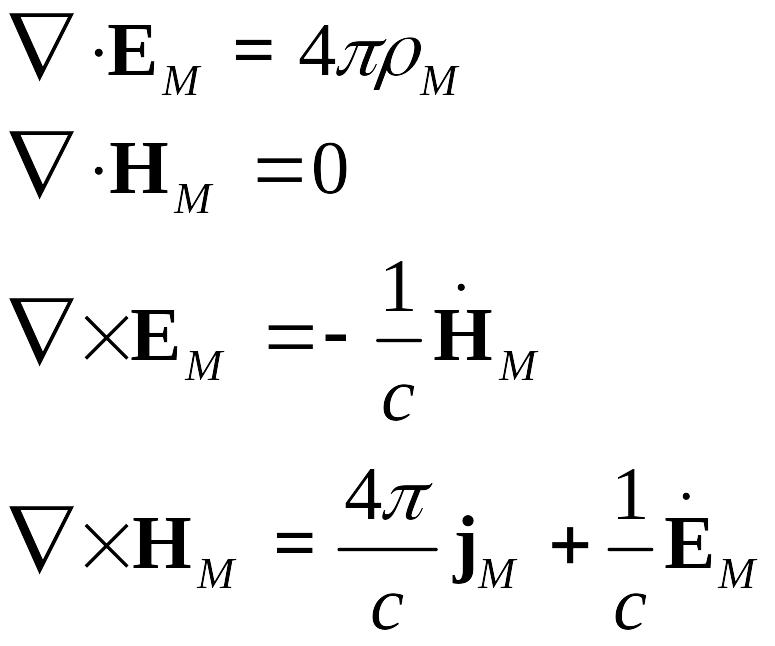
включает в себя как связанные, так и
свободные заряды в веществе. Каждой
точке пространства ставится в соответствие
функция
.
Это значит, что мы заменяем реальную
среду моделью – сплошной средой, т.е.
мы свойства разных точек «размазываем»
по пространству. Существуют следующие
способы описания сплошной среды на
основе реальной среды:
Усреднение по некоторому физическому объёму
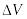и
времени
.Статистическое усреднение. Считаем, что у нас есть макроскопически идентичный ансамбль систем (т.е. все внешние условия одинаковы). Здесь производятся измерения для отдельных ансамблей, а потом происходит усреднение. Этот способ более предпочтителен.
Усреднение будем обозначать символами «< >». Отметим, что усреднение коммутативно с дифференциальными операторами.
Итак, усредняем:
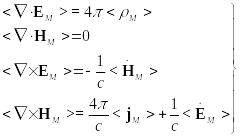
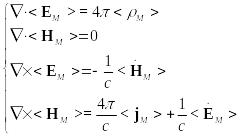
Среда под действием внешнего
электромагнитного поля поляризуется,
т.е. реагирует на внешнее воздействие.
В случае, когда отсутствует пространственная
дисперсия, поляризация характеризуется
векторами электрической и магнитной
поляризации
.
Можно показать, что
и
выражаются через
:
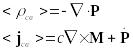
Введём обозначения:
;
Перенесём второе слагаемое из правой
части в левую и объединим его с
:
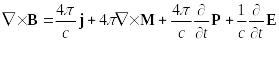
Итак, уравнения Максвелла для среды имеют вид:
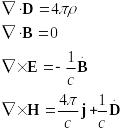
§9. Материальные уравнения или уравнения связи.
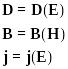
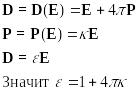
Здесь
- диэлектрическая проницаемость, а
-
диэлектрическая восприимчивость.
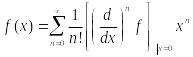-разложение
функции
в
ряд Маклорена.
Если же :
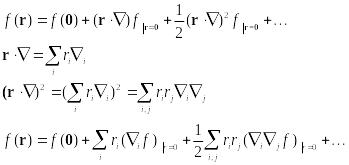
Возможно разложить
по векторам
в
ряд Маклорена:
Первое слагаемое – это индукция, связанная с собственным дипольным моментом в отсутствие внешнего поля (собственная поляризация) – пироэлектричество.
Второе слагаемое – линейные среды.
Третье слагаемое – учёт нелинейности среды.
Среды, для которых нелинейные члены в разложении индукции по полю имеют вес, называются нелинейными.
Линейные среды
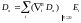
Введём обозначение:
,
тогда
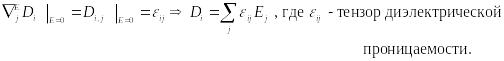
Аналогично вводятся тензоры:
Для ферромагнетиков
-
учёт нелинейности.
Неоднородные среды
Среды, для которых материальные
характеристики (
)
являются функциями координат.
Т.е. характеристики трансляционно не инвариантны.
Введём понятие сплошной среды. Сплошная среда – это среда, в каждой точке которой измерение материальных характеристик даёт не нулевой результат. Сплошная среда – это модель. В реальной среде имеются микро-пустоты, т.е. вещество локализовано в некоторых точках пространства. Чтобы перейти к сплошной среде, нужно усреднить микропараметры по достаточно большому объёму.
Анизотропные среды
Анизотропные среды (свойства), это такие среды, свойства которых зависят от направления, в котором это свойство измеряется.
П
усть
в каком-то направлении исследуются
оптические свойства среды. Затем мы
повернули направление исследования, и
оптические свойства изменились, т.е.
оптические свойства зависят от угла
поворота.
Так как свойства меняются, то они не инвариантны относительно вращения. Этим свойством обладает всякая анизотропная среда.
Для тензоров 2-го ранга есть исключения:
Кубические системы описываются тензорами изотропного вида, т.е.
Монокристалл – есть однородная анизотропная среда.